Пусть А – случайное событие, вероятности появления и непоявления

Лекция 55. Повторения независимых испытаний. Формула Бернулли. Локальная и интегральная теоремы Лапласа.

которого для некоторого испытания известны:

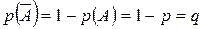; ; (1)

И пусть производится не одно, а n повторных испытаний (или, что одно и то же, испытание повторяется n раз). Возникает естественный вопрос: какова вероятность того, что событие А в этих n повторных испытаниях появится k раз (целое число k можно задавать любым в пределах от 0 до n)? При этом не важно, в каком порядке событие А появится k раз в n испытаниях. Важно лишь общее число k появлений этого события. Эту вероятность обозначают символом (- вероятность того, что в n испытаниях событие А наступит k раз). И находится она по формуле Бернулли (Яков Бернулли – швейцарский математик 17-го века):

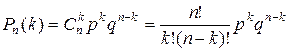(2)

Доказательство. Если в n повторных испытаниях событие А появится k раз, то соответственно оно не появится n-k раз. И тогда вероятность любой конкретной комбинации k появлений события А и n-k непоявлений этого события можно найти по формуле произведения вероятностей независимых в совокупности событий. То есть она равна 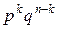. Таких конкретных комбинаций будет, очевидно, столько, сколько существует сочетаний из n элементов (номеров испытаний) по k элементов в каждом сочетании. Эти сочетания образуются из k номеров тех испытаний, в которых будет появляться событие А. Каждому такому сочетанию k номеров будет соответствовать единственное сочетание тех n-k номеров испытания, в которых событие А не будет появляться. Так как всего таких сочетаний 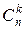, и каждое из них несовместно с любым другим сочетанием, то по формуле сложения вероятностей попарно несовместных событий искомая вероятность равна величине 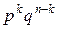, взятой 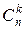раз. В итоге и приходим к формуле Бернулли (2).

Пример 1. Монету подбрасывают пять раз подряд. Какова вероятность того, что при этом герб выпадет ровно три раза?

Решение. Будем считать испытанием однократное подбрасывание монеты. Тогда n=5 – число повторных испытаний. Далее, будем считать событием А в каждом испытании (при каждом бросании монеты) выпадение герба. Тогда

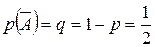; ; n=5; k=3;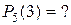

На основании формулы Бернулли получаем:

.

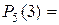
Формула Бернулли – точная формула. Однако при больших значениях n (большом числе испытаний) вычисления по ней становятся громоздкими из-за необходимости вычисления факториалов больших чисел и степеней с большими показателями. В процессе этих вычислений неизбежно придется производить округления, что приведет к погрешности при определении искомой вероятности . Причем к погрешности тем большей, чем больше будет значение n (числа испытаний). В связи с этим из формулы Бернулли выведены упрощенные приближенные формулы для , которые, кстати, тем точнее, чем больше число n.

Одна из этих приближенных формул – локальная формула Лапласа:

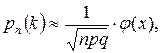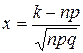где (3)

Дата добавления: 2013-12-13