Дискретные случайные величины и их числовые характеристики

Дискретная случайная величина Х считается заданной, если известен список (х₁; х₂; x_3; … х_n) всех её возможных значений, а также известны вероятности (р₁; р₂; p_3; … р_n) принятия ею этих её возможных значений. Эти данные оформляются в виде таблицы,

X	х1 х2 x3 ……хn	(1)
p	р1 р2 p3 ……рn

которая называется законом распределения дискретной случайной величины Х.

Отметим, что сумма вероятностей р₁+р₂+…+р_n представляет собой, согласно формуле для попарно несовместных событий, вероятность принятия случайной величиной Х хотя бы одного из своих возможных значений (или х₁, или х₂, … или x_n). То есть представляет собой вероятность достоверного события – события, которое произойдет обязательно. Но вероятность достоверного события равна единице. Таким образом:

р₁+р₂+…+р_n =1 (2)

Это равенство должно выполняться в любом законе распределения (1).

Информация о распределении, представленная на графике точками с координатами () и соединяющей их ломаной, называется многоугольником (полигоном) распределения.

Вероятность того, что случайная величина 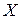примет значение, меньшее , называется функцией распределения 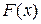, т. е. . Для ДСВ

.

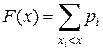Пример 4. В лотерее разыгрываются 200 лотерейных билетов. Из них 2 билета содержат выигрыш по 1000 рублей, 5 билетов по 500 рублей, 10 билетов по 300 рублей и 25 билетов по 100 рублей. Составить закон распределения дискретной случайной величины Х – выигрыша для владельца одного лотерейного билета.

Решение. Искомый закон распределения очевиден:

Х
р	0,79	0,125	0,05	0,025	0,01

Пример 5. Батарея состоит из 3 орудий. Вероятность попадания в цель при одном выстреле для первого орудия 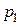= 0,5; для второго = 0,6; для третьего — 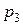= 0,8. Все орудия делают по одному выстрелу. Охарактеризовать случайную величину Х — число попаданий в цель.

Очевидно, что Х может принять одно из четырех значений: 0, 1, 2, 3.

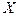= 0, если ни одно орудие не попадет;

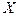= 1, если попадет одно орудие (либо первое, либо второе, либо третье); 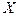= 2, если попадут два орудия: либо первое и второе, либо первое и третье, либо второе и третье;

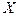= 3, если попадут все три орудия.

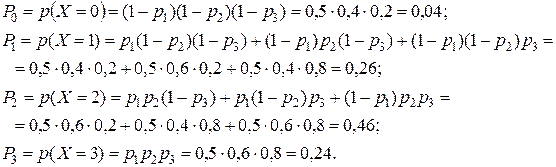
Сделаем проверку: .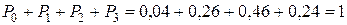

Выпишем ряд распределения

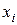
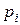
	0,04	0,26	0,46	0,24

Полигон распределения представлен на рисунке. Функция распределения представлена таблицей и графиком.

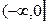
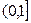
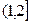
		0,04	0,3	0,76

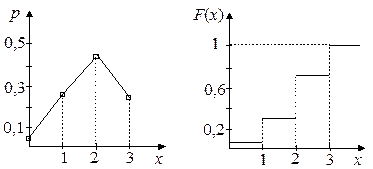
Данный пример иллюстрирует следующие свойства функции распределения ДСВ (которые можно легко доказать, учитывая, что вероятность любого события заключена в пределах от 0 до 1).

1) 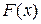– ступенчатая разрывная функция;

2) 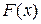– неубывающая функция (т. е. либо возрастает, либо постоянна);

3) 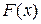= 0, для всех , где – наименьшее из всех значений ;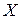

4) 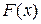= 1, для всех , где – наибольшее из всех значений .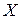

Приведенные характеристики дают полное и ясное представление о случайной величине. Однако, в случае, когда ДСВ имеет много значений (десятки, сотни и т. д.) они будут очень громоздкими и требуют много места. Кроме того, во многих практических задачах вовсе нет необходимости так подробно описывать случайную величину.

На практике обычно важно знать не столько сам закон распределения дискретной случайной величины (таблицу), сколько некоторые суммарные (обобщающие) числовые характеристики этой случайной величины, характеризующие её в целом. В частности, на практике наиболее важно знать:

а) среднее значение х_ср случайной величины;

б) степень разброса её возможных значений (х₁; х₂; … х_n) вокруг её среднего значения х_ср.

Начнем с того, что найдем среднее значение х_ср дискретной случайной величины Х. Пусть таблица (1) – закон её распределения. Представим себе, что будет проведено N повторных испытаний. Так как (р₁; р₂; … р_n) – вероятности появления значений (х₁; х₂; … х_n) случайной величины Х, то согласно формуле 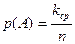эти значения появятся в среднем (р₁N; p₂N; … p_nN) раз соответственно. Тогда среднее из всех этих N значений будет, очевидно, таким:

х_ср = (3)

Это среднее значение дискретной случайной величины Х является наиболее ожидаемым её значением для каждого отдельного испытания, и потому называется математическим ожиданием случайной величины Х. Оно обозначается символом М(Х). Итак,

М(Х)=х_ср = (4)

- математическое ожидание (среднее значение) дискретной случайной величины Х. Вокруг математического ожидания группируются реальные средние значения случайной величины Х в различных сериях испытаний.

Дата добавления: 2013-12-13