Лекция 6. Контур с током в магнитном поле. Циркуляция вектора В. Магнитные поля соленоида и тороида

Контур с током в магнитном поле. Если замкнутый контур, по которому течет ток, помещен в однородное магнитное поле, то сила Ампера, действующая на контур в целом, равна нулю. Действительно, пусть В = const. Тогда результирующая сила Ампера получится интегрированием выражения (62) вдоль замкнутого контура, причем условие постоянства В позволяет внести интеграл в скобки векторного произведения

.

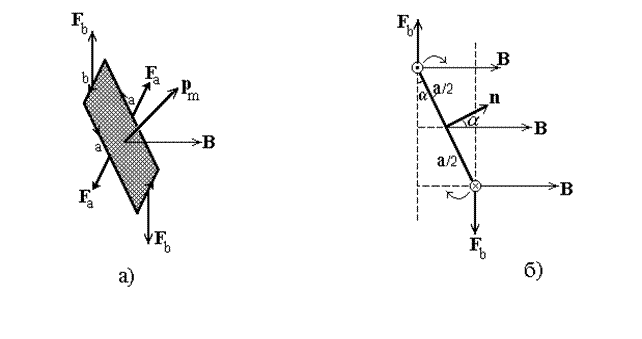
Интеграл 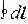=0, поскольку он является суммой векторов d l, присоединенных друг за другом по правилу: “голова к хвосту”. Причем “хвост” первого вектора совпадает с “головой” последнего. Поэтому интеграл равен нулю, следовательно равна нулю и сила F.

Рис.21

Поместим прямоугольную рамку из тонкого провода, по которому течет ток I в однородное магнитное поле с индукцией В (рис.21). Так как сила, действующая на контур в целом, равна нулю, рамка как целое перемещаться не будет. Однако она может вращаться, если на нее действует отличный от нуля суммарный момент сил, который легко вычислить. На рис.21 а стороны рамки длиной b расположены перпендикулярно вектору В, а стороны длиной a - под произвольным углом. На каждую сторону рамки будет действовать своя сила Ампера: на стороны a F _a= I [ a ´ B ]; на стороны b F _b= I [ b ´ B ], где векторы a и b имеют направление тока на своем участке. Поскольку силы F _a равны по модулю и направлены в противоположные стороны, они будут растягивать рамку.

Для удобства вычислений изобразим рамку так, чтобы стороны b были перпендикулярны плоскости листа (рис.21 б). Пара сил F _b, действующих на стороны b создает момент величиной

M = IbBa × sina = IBab sina, (65)

где a - угол между плоскостью рамки и вертикалью. Угол между векторами n и В также равен a, так как это углы со взаимно перпендикулярными сторонами.

Введем вектор магнитного момента контура с током р _m. Это вектор, направленный вдоль нормали n к плоскости контура (выбранной так, чтобы она составляла правовинтовую систему с направлением тока в контуре), а по модулю, равный произведению тока в контуре на его площадь:

p_m = IS = Iba. (66)

Выразим момент сил (65) через магнитный момент

M = IBab sina = IB S sina = IS Bsina, Þ

M = [ I S´B ] = [ p _m ´B ]. (67)

Этот момент будет поворачивать рамку так, чтобы векторы p _m и B стали параллельны.

Если вектор p _m перпендикулярен B (a = p/ 2), то момент M - максимален, и рамка будет поворачиваться по полю до тех пор, пока они не станут параллельны. Поскольку также ведет себя магнитная стрелка, можно считать, что вектор p _m описывает магнитные свойства контура с током. Если p _m параллелен B, то момент M равен нулю и силы Ампера либо сжимают контур, либо растягивают в зависимости от направления тока в нем.

Пусть плоский контур с током - не прямоугольный. Тогда элемент d l контура произвольной формы можно разложить на две составляющие: параллельную вектору B и перпендикулярную. На первую из них, в соответствии с выражением (62), сила Ампера не будет действовать, а вторая будет вести себя, как сторона b прямоугольной рамки с током. Поэтому в однородном магнитном поле любой плоский контур с током будет поворачиваться, стремясь установиться своим магнитным моментом по полю.

Энергия контура с током в магнитном поле. Чтобы повернуть контур с током в магнитном поле на угол da необходимо приложить внешний момент сил N, направленный противоположно М. Как известно из курса механики, при этом внешние силы совершают работу dA = Nda = p _m× Bsina da. Эта работа идет на увеличение потенциальной энергии dW_p = dA, следовательно,

dW_p = p _m× Bsina da. (68)

Интегрируя, получаем выражение для потенциальной энергии

.

Положим const =0, что физически соответствует энергии контура, удаленного от места локализации поля на бесконечность. Тогда потенциальная энергия контура с током в магнитном поле

W_p = - p _m× B×cosa = - (p _m, B). (69)

Рис.22

Контур с током в неоднородном магнитном поле. Поместим контур перпендикулярно силовым линиям неоднородного магнитного поля (рис.22), которое возрастает только в направлении оси x. На каждый элемент d l контура с током будет действовать сила Ампера d F, направленная под острым углом к плоскости контура в сторону уменьшения x (при указанном направлении тока), поэтому результирующая сила направлена противоположно оси x - против наибыстрейшего изменения В. Вычислим величину F_x - силы действующей вдоль оси x

F_x = - ¶ W_p/¶ x = p_m cosa ¶B/¶ x. (70)

Таким образом, контур с током в неоднородном магнитном поле будет втягиваться в область более слабого поля (или сильного), в зависимости от направления тока в контуре. Кроме того, он будет поворачиваться своим магнитным моментом по полю, а также растягиваться или сжиматься.

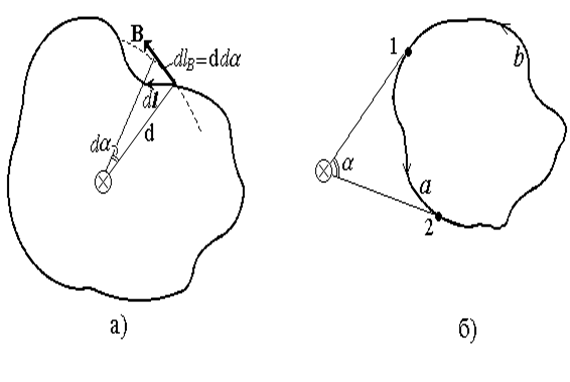
Циркуляция вектора В. Вычислим циркуляцию вектора магнитной индукции для длинного прямого проводника с током I вдоль плоского контура, перпендикулярного проводу. На рис.23а контур лежит в плоскости листа и охватывает ток. Проводник создает на расстоянии d от него магнитное поле (64), направленное перпендикулярно проводу по касательной к окружности радиуса d. Обозначим dl_B проекцию элемента d l контура на направление вектора В. Если эта проекция видна под углом da, то dl_B = d× da. Следовательно,

.

Для вычисления циркуляции достаточно проинтегрировать это выражение по a в пределах от 0 до p

.

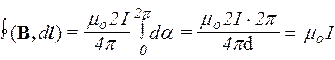Рис.23

Если проводник расположен вне контура (рис.23 б), то интеграл по замкнутому контуру может быть представлен суммой интегралов, взятых вдоль частей (а) и (б) контура, на которые его делят касательные, проведенные от проводника

.

Если контур не лежит в плоскости, перпендикулярной току, то любой его элемент d l можно разложить на составляющие: d l ₁ - перпендикулярную току, и d l ₂ - параллельную. Тогда (В, d l ₂)=0, так как угол между векторами В и d l ₂ равен p/ 2. Поэтому для неплоского контура получится тот же результат.

Теперь остается рассмотреть случай, когда контур охватывает несколько токов. Тогда, вычислив циркуляцию для каждого тока и сложив их, окончательно имеем

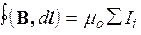. (71)

Циркуляция вектора магнитной индукции вдоль произвольного замкнутого контура равна алгебраической сумме токов, охватываемых контуром, умноженной на m_о. Это утверждение называют теоремой о циркуляции вектора В или законом полного тока. За положительное направление тока принято выбирать такое, которое связано с направлением обхода контура правилом правого винта.

Рис.24

Магнитное поле тороида. Тороидом называется обмотка из тонкого провода, намотанная на каркас в форме тора (рис.24). Пусть внутренний радиус тороида R₁, внешний – R₂, средний - R. В качестве замкнутого контура выберем сначала окружность радиуса r < R₁. Если витки плотно прилегают друг к другу, магнитную индукцию во всех точках выбранной окружности можно считать одинаковой и направленной по касательной к ней. Поскольку внутри окружности нет токов, по теореме о циркуляции имеем = В× 2 pr =0, поэтому и В=0. При r > R₂ алгебраическая сумма токов равна нулю, так как ток каждого витка проходит внутри контура дважды в противоположных направлениях.

При R₁<r< R₂ 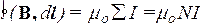= m_o×n 2 pR×I, где N - полное число витков тороида, n - приходящееся на единицу длины: N=n 2 pR. Поскольку ,

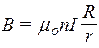. (72)

Для тороида, радиус которого R>>R₂-R₁, r» R, поэтому В=m_onI.

Рис. 25

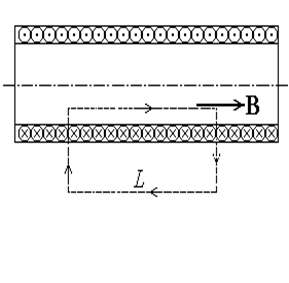
Магнитное поле соленоида. Рассчитаем поле соленоида в двух приближениях: в грубом, а затем в более точном. Соленоид представляет собой тонкий проводник, намотанный по винтовой линии на цилиндрическую поверхность. Пусть по проводнику течет ток I и на единицу длины соленоида приходится n витков, а шаг винтовой линии настолько мал, что каждый виток можно считать замкнутым и плоским. Опыт и расчет показывают, что чем длиннее соленоид, тем меньше индукция магнитного поля снаружи от него. В пределе полагают поле вне соленоида равным нулю. Из соображений симметрии ясно, что вектор В внутри соленоида направлен вдоль его оси. Выберем прямоугольный контур, как показано на рис.25. Циркуляция по данному контуру равна Вl и контур охватывает ток nlI. По теореме о циркуляции Вl=m_onlI, следовательно, магнитное поле внутри соленоида

B=m_onI. (73)

Это поле однородно, за исключением окрестности торцов, где, как показывает расчет, В=m_оnI/2.

Теперь учтем, что проводник намотан по винтовой линии. Простейшей моделью, отвечающей этому приближению, будет соленоид радиуса а, намотанный вплотную проводником в виде ленты шириной h. На рис.26 дана развертка одного витка, разрезанного параллельно оси соленоида. Введем вектор линейной плотности тока i, направленный вдоль ленты, модуль которого i=I/h. Разложим его на две составляющие: i _^ - перпендикулярную оси соленоида и i _║ - параллельную

i = i _^ + i _║.

Пусть a - угол между шириной ленты и осью соленоида. Тогда

i _^= i×cosa =,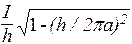

i _^= i×sina=.

Рис.26

Магнитную индукцию В _i внутри соленоида будет определять i _^, а i _║- будет определять поле В _a вне соленоида. По теореме о циркуляции для прямоугольного контура (такого, как на рис. 25), получим

B_ih/cosa=m_oI, Þ , Þ

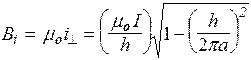. (74)

Для вычисления индукции поля В _a вне соленоида выберем контур в виде окружности радиуса r>a, перпендикулярной оси соленоида. По теореме о циркуляции

B_a 2 p r= m_oI, Þ B_a = m_oI/ 2 pr,Þ

. (75)

Из формул (74) и (75) следует, что при отношении радиуса соленоида к ширине ленты a/h ~10 поле внутри соленоида В_i больше поля снаружи В_a в 2p×10 раз. Причем поле вне соленоида подобно полю прямого тока.

Поток вектора магнитной индукции В. Теорема Гаусса для вектора Е указывает на заряды как источники электростатического поля. Магнитное поле не имеет специальных "магнитных" источников.

Теорема Гаусса для вектора В постулирует этот факт следующим образом

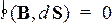. (76)

Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю. Поэтому силовые линии вектора В замкнуты сами на себя, и число линий, выходящих из любого объема, ограниченного замкнутой поверхностью S, равно числу линий, входящих в этот объем.

В заключение приведем небольшую таблицу, где сопоставлены свойства постоянных электрического и магнитного полей в вакууме.

Таблица 1
Электрическое поле	Магнитное поле
Источниками электрического поля являются заряды	Магнитное поле не имеет источников
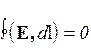
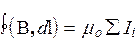
Поле потенциально	Поле не потенциально

Дата добавления: 2013-12-13