
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение параметров функциональных зависимостей
|
|
|
|
1) Определение параметров линейной зависимости 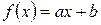 .
.
Параметры 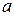 и
и 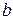 должны быть такими, чтобы величина
должны быть такими, чтобы величина 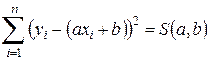 была минимальной. Используем необходимое условие минимума функции
была минимальной. Используем необходимое условие минимума функции 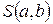 :
:
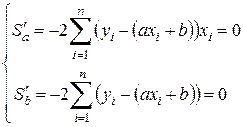
Преобразование написанных условий приводит к следующей системе для определения 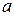 и
и 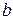 :
:
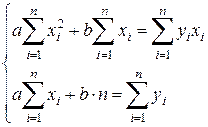
Решая эту систему, получаем формулы:
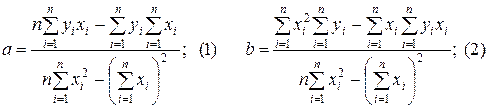
2) Определение параметров экспоненциальной зависимости 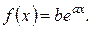
Прологарифмируем функцию 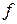 :
: 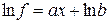
Зависимость 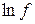 от x линейная, поэтому заменим в формулах (1) и (2)
от x линейная, поэтому заменим в формулах (1) и (2) 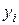 на
на 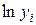 , а
, а 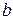 на
на 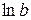 :
:
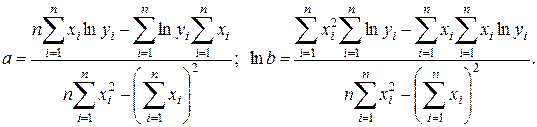
Окончательно находим 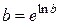 .
.
3) Определение параметров логарифмической зависимости 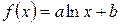 .
.
Отличие данной формулы от линейной состоит в замене 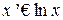 , поэтому:
, поэтому:
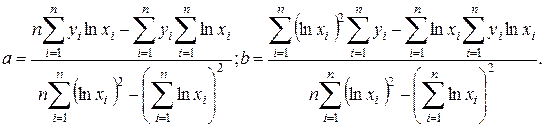
4) Определение параметров гиперболической зависимости 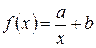 .
.
В данной формуле, в отличие от линейной, x заменен на 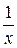 , поэтому
, поэтому
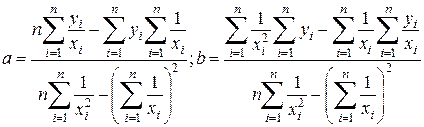
5) Определение параметров квадратичной зависимости 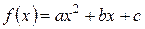 .
.
Составим 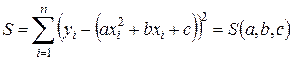 .
.
Необходимое условие минимума функции 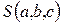 :
:
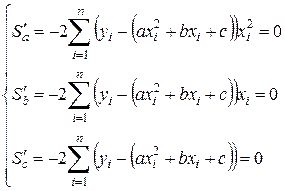
Преобразование выписанных уравнений приводит к системе

| xi | ||||||||||
| yi | –0,6 | 1,1 | 2,7 | 3,7 | 5,9 | 7,1 | 8,3 | 10,5 | 11,5 | 12,8 |
| yi | ||||||||||
| yi | 7,5 | 2,5 | 0,5 | 1,1 | –0,5 | –1,2 | –1,2 | –1,7 | –1,5 | –1 |
Пример. Даны три набора значений функции 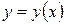 . Представить их на графике и выбрать вид функции, наилучшим образом описывающей каждую зависимость. С помощью метода наименьших квадратов найти числовые параметры выбранных функциональных зависимостей.
. Представить их на графике и выбрать вид функции, наилучшим образом описывающей каждую зависимость. С помощью метода наименьших квадратов найти числовые параметры выбранных функциональных зависимостей.
|
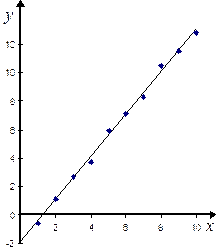
Исследуем первую зависимость, представленную первой и второй строками таблицы. Нанесем табличные данные на график.
Расположение точек ближе всего к графику линейной функции – прямой. Поэтому для первой зависимости выбираем функцию
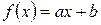 .
.
Вычислим суммы:
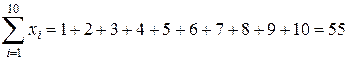 ;
;
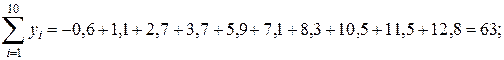
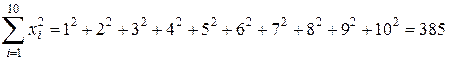 ;
;
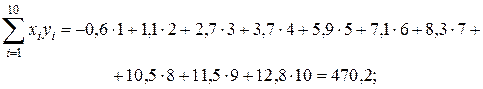
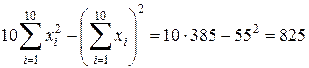 .
.
Используя формулы (1) и (2) из раздела 6.5 найдем
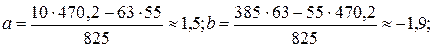
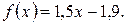
Нанесем прямую, описываемую данной функцией, на график по двум точкам:
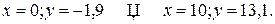
Табличные точки располагаются вблизи полученной прямой, значит вид функции выбран удачно.
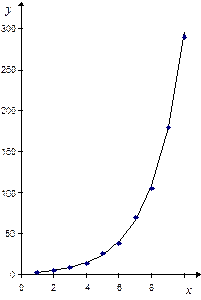
2) Исследуем вторую зависимость, представленную первой и третьей строками таблицы. Нанесем табличные данные на график.
|
Расположение точек позволяет сделать вывод: функция при малых значениях переменной (x < 5) меняется слабо, а при больших значениях – резко возрастает, что свидетельствует в пользу выбора экспоненциальной зависимости
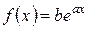 .
.
Проведем необходимые вычисления.
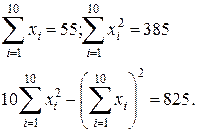

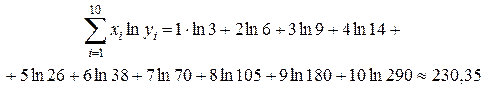
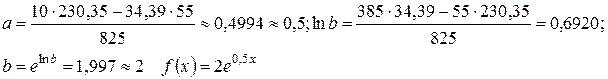
Заполним таблицу значениями функции.
| x | ||||||||||
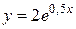
| 3,3 | 5,4 | 9,0 | 14,8 | 24,4 | 40,2 | 66,2 | 109,2 | 180,0 | 296,8 |
Нанесем полученные точки на график и соединим плавной линией, которая весьма удовлетворительно соответствует исходным данным.
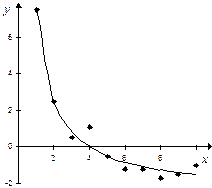
|
3) Исследуем третью зависимость, представленную первой и четвертой строками таблицы. Нанесем табличные данные на график. Сильное изменение функции при небольших 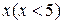 и очень незначительное при больших
и очень незначительное при больших 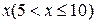 указывает на возможность выбрать для данного случая гиперболическую зависимость
указывает на возможность выбрать для данного случая гиперболическую зависимость 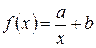 .
.
Выполним необходимые вычисления:
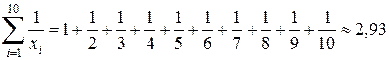 ;
;
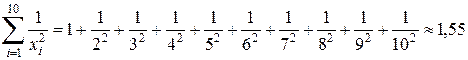 ;
;
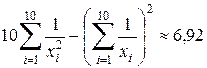 ;
;
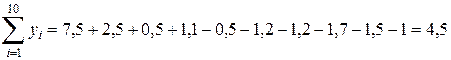 ;
;
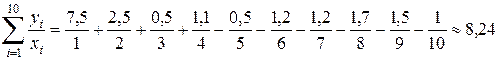 ;
;
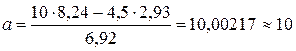 ;
;
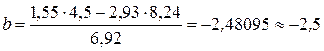 ;
;
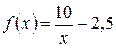 .
.
Составим таблицу значений функции.
| x | ||||||||||
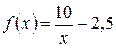
| 7,5 | 2,5 | 0,8 | 0,0 | –0,5 | –0,8 | –1,1 | –1,3 | –1,4 | –1,5 |
Нанесем рассчитанные значения на график и соединим плавной линией. Точки, соответствующие исходным данным хорошо группируются вблизи проведенной линии, значит, зависимость выбрана удовлетворительно.
|
|
|
Дата добавления: 2013-12-13; Просмотров: 1555; Нарушение авторских прав?; Мы поможем в написании вашей работы!