Линейная зависимость двух геометрических векторов

Линейные операции над векторами.

Геометрические векторы. Операции над векторами.

8.1. Основные понятия. Геометрическим вектором (или просто вектором) будем называть направленный отрезок. Обозначать его будем 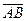, где 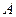- начало вектора, - конец вектора, или одной буквой . Начало вектора называют еще точкой приложения вектора. Длину вектора будем обозначать, используя знак модуля: или .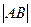

Вектор называется нулевым, если его начало и конец совпадают.

Определение. Векторы называются коллинеарными, если они лежат на параллельных прямых.

Определение. Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и направление.

Все нулевые векторы считаются равными.

Очевидно, что для любого вектора и любой точки существует и притом единственный вектор с началом в точке , равный вектору .

Все множество векторов можно разбить на классы равных векторов. Каждый такой класс будем называть свободным вектором. Впредь под вектором мы будем понимать, как правило, свободный вектор.

А). Сложение векторов.

Определение. Суммой двух векторов и называется вектор, идущий из начала вектора в конец вектора при условии, что вектор приложен к концу вектора (правило треугольника).

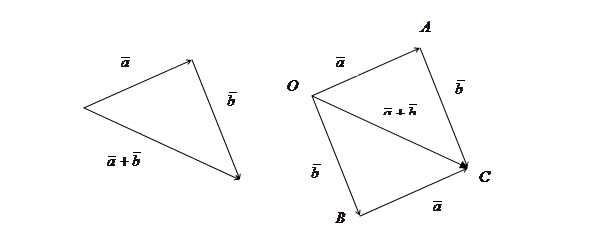
Свойства операции сложения:

1) (коммутативность);

2) 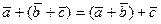(ассоциативность);

3) для любого вектора , где - нулевой вектор;

4) для любого вектора существует вектор такой, что (существование противоположного вектора).

Свойства 3) и 4) очевидны и вытекают непосредственно из определения операции сложения векторов. Для доказательства свойства 1) построим параллелограмм:

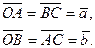
Тогда

Значит, .

Заметим, мы заодно получили правило параллелограмма сложения двух векторов.

Теперь докажем свойство 2). Возьмем произвольную точку . Приложим вектор к точке , вектор - к концу вектора , вектор 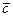- к концу вектора . Тогда:

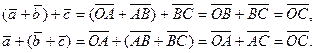
Значит, .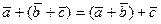

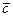Пользуясь свойствами 1)-4), легко определить разность векторов и : это такой вектор , который в сумме с вектором дает вектор . Этот вектор 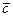равен , где - вектор, противоположный вектору . Действительно,

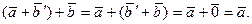
Убедимся в единственности вектора 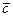с условием . Пусть существует вектор 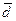такой, что . Тогда

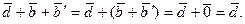
В то же время

Значит, .

Б). Умножение вектора на число.

Определение. Произведением вектора на число называется вектор, коллинеарный вектору , имеющий длину и направление, совпадающее с направлением при и противоположное 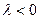при . При .

Свойства операции умножения на число:

1) ;

2) ;

3) .

Эти свойства знакомы вам еще со школы. Их доказательства очень просты. Так для доказательства первого свойства достаточно увидеть, что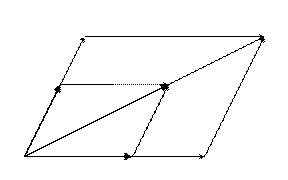 треугольник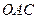и и подобны (по двум сторонам и углу между ними). Значит, , т.е. .

Для доказательства второго и третьего свойств заметим, что векторы в левой и правой частях равенства коллинеарны. Равенство их длин легко получить, рассмотрев различные сочетания знаков чисел и .

Выполнение свойств операций сложения и умножения на число означает, что множество свободных векторов образует линейное пространство (вспомните определение и сравните).

Теорема 1. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Доказательство. 1) Пусть векторы и линейно зависимы., т.е. существуют числа и 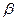, одновременно не равные нулю, такие, что

.

Пусть для определенности . Тогда

.

Если обозначить 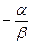через , получим

.

По определению произведения вектора на число и коллинеарны.

2). Докажем обратное. Пусть и коллинеарны. Если один из векторов нулевой, то они линейно зависимы. Если оба вектора ненулевые, то возьмем 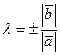, а знак выберем в зависимости от направления:: +, если и сонаправлены, и -, если они имеют противоположные направления. Тогда и, следовательно, , т.е. и линейно зависимы. Теорема доказана.

Дата добавления: 2013-12-13