
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейная зависимость четырех векторов
|
|
|
|
Теорема 3. Любые четыре вектора линейно зависимы.
Доказательство. Если среди четырех векторов есть три компланарных, то теорема доказана. Предположим, что никакие три вектора из четырех не компланарны. Приложим все векторы – обозначим их  ,
,  ,
, 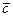 и
и 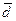 - к общему началу, точке
- к общему началу, точке  .
.
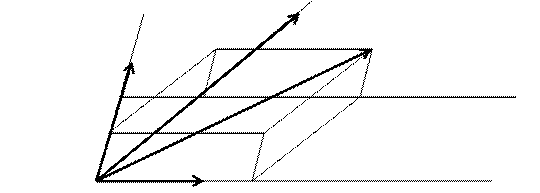
Плоскости, в которых лежат векторы  и
и  ,
,  и
и 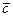 ,
,  и
и 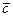 различны. Через конец вектора
различны. Через конец вектора 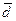 проведем плоскости, параллельные этим трем плоскостям, и найдем их точки пересечения с прямыми, на которых лежат векторы
проведем плоскости, параллельные этим трем плоскостям, и найдем их точки пересечения с прямыми, на которых лежат векторы  ,
,  и
и 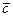 .Получили параллелепипед. Заметим, что
.Получили параллелепипед. Заметим, что
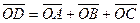 ,
,
но  ,
,  ,
, 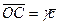 , значит,
, значит,
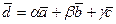 ,
,
откуда
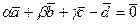 ,
,
т.е. векторы  ,
,  ,
, 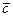 и
и 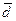 линейно зависимы. Теорема доказана.
линейно зависимы. Теорема доказана.
Попутно мы доказали, что для любой тройки некомпланарных векторов  ,
,  и
и 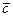 и для любого вектора
и для любого вектора 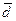 найдутся числа
найдутся числа 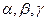 , такие, что
, такие, что 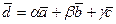 .
.
8.6. Аффинные координаты. Декартовы прямоугольные координаты. Как и в любом векторном пространстве, в пространстве свободных векторов существует понятие базиса. Напомним, что упорядоченный набор векторов образует базис, если:
1) эти векторы линейно независимы,
2) любой вектор в пространстве линейно выражается через них.
Теорема 4. Любая упорядоченная тройка некомпланарных векторов образует базис в пространстве.
Доказательство теоремы очевидно: любые три некомпланарных вектора линейно независимы и любой вектор является их линейной комбинацией. Справедлива также
Теорема 4а. Любые два неколлинеарных вектора, лежащие в плоскости, образуют базис в этой плоскости.
Напомним, что равенство
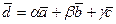
называют разложением вектора 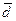 по базису
по базису 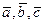 , а числа
, а числа 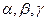 - координатами вектора
- координатами вектора 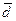 в базисе
в базисе 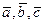 . Эти координаты определены однозначно.
. Эти координаты определены однозначно.
Зафиксировав базис 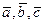 в пространстве свободных векторов и точку
в пространстве свободных векторов и точку  в пространстве – ее называют началом координат, - мы можем определить так называемые аффинные координаты произвольной точки
в пространстве – ее называют началом координат, - мы можем определить так называемые аффинные координаты произвольной точки  нашего пространства.
нашего пространства.
Определение. Аффинными координатами точки  пространства называются координаты вектора
пространства называются координаты вектора 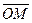 .
.
Так как каждый вектор может быть разложен по фиксированному базису, причем это разложение однозначно, то аффинные координаты каждой точки однозначно определены.
Пусть в пространстве заданы две точки своими аффинными координатами: 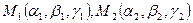 . Тогда координаты вектора
. Тогда координаты вектора 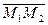 находятся следующим образом:
находятся следующим образом:
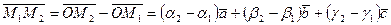 /
/
Частным случаем аффинных координат являются декартовы прямоугольные координаты, когда базисные векторы имеют единичную длину и взаимно перпендикулярны. В этом случае базисные векторы принято обозначать 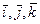 . Если
. Если
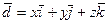 ,
,
то обычно записывают
 .
.
Оси, проходящие через начало координат и параллельные векторам 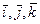 , называют координатными осями.
, называют координатными осями.
Чтобы выяснить геометрический смысл декартовых прямоугольных координат, введем понятие проекции вектора на ось.
Пусть 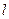 - некоторая ось (прямая с выбранным на ней направлением). Приложим вектор
- некоторая ось (прямая с выбранным на ней направлением). Приложим вектор  к произвольной точке
к произвольной точке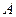 :
:  Из точек
Из точек 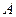 и
и  опустим на прямую
опустим на прямую 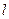 перпендикуляры. Их основания – точки
перпендикуляры. Их основания – точки 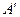 и
и  соответственно. Проекцией вектора на ось будем называть длину отрезка
соответственно. Проекцией вектора на ось будем называть длину отрезка 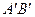 , взятую со знаком +, если
, взятую со знаком +, если 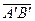 и
и 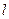 имеют одно и то же направление, и со знаком - в противном случае.
имеют одно и то же направление, и со знаком - в противном случае.
Обозначение: пр l .
.

Теорема 5. Декартовы прямоугольные координаты вектора равны проекциям этого вектора на координатные оси.
Доказательство. Приложим произвольный вектор  к началу координат
к началу координат  и проведем через его конец три плоскости, перпендикулярные координатным осям. Точки
и проведем через его конец три плоскости, перпендикулярные координатным осям. Точки  - точки пересечения этих плоскостей с осями.
- точки пересечения этих плоскостей с осями.

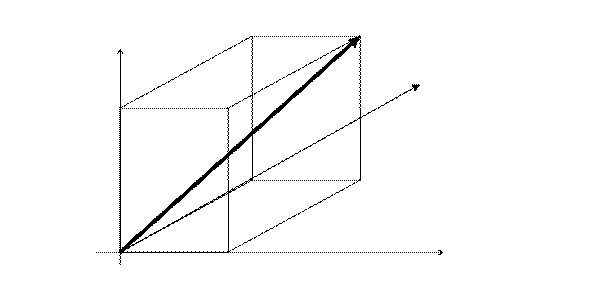
Тогда 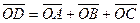 . Но
. Но 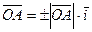 , причем знак выбирается в соответствии с тем, совпадают или нет направления
, причем знак выбирается в соответствии с тем, совпадают или нет направления 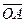 и
и 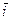 . Иначе,
. Иначе, 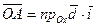 . Аналогично,
. Аналогично,
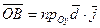 ,
, 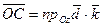 . Теорема доказана.
. Теорема доказана.
Замечание 1. Рассмотрим треугольник 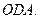 В нем угол
В нем угол 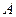 прямой. Пусть
прямой. Пусть
 . Тогда если угол
. Тогда если угол  острый, то
острый, то
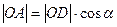 .
.
Если угол  тупой, то
тупой, то
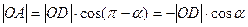 .
.
Отсюда  . Аналогично получаем, что
. Аналогично получаем, что 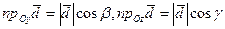 , где
, где 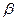 - величина угла
- величина угла 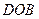 ,
,  - величина угла
- величина угла  . Итак,
. Итак,
 .
.
Величины 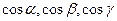 называют направляющими косинусами. Значит, вектор однозначно определяется своей длиной и направляющими косинусами.
называют направляющими косинусами. Значит, вектор однозначно определяется своей длиной и направляющими косинусами.
Замечание 2. Пусть  . Воспользовавшись теоремой Пифагора, получим:
. Воспользовавшись теоремой Пифагора, получим:
 .
.
Отсюда следует, во-первых, что
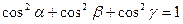 ,
,
и, во-вторых, что
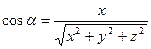 ,
,
 ,
,
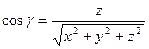 .
.
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 6264; Нарушение авторских прав?; Мы поможем в написании вашей работы!