Лекция № 13 Основные элементарные функции: постоянная, степенная, показательная, логарифмическая, тригонометрические, обратные тригонометрические функции

Лекция № 12. Понятие функции одной переменной. График функции. Способы задания функций. Понятие сложной функции и обратной функции. Ограниченность, монотонность, четность и нечетность, периодичность функций.

Переправа вплавь

Переправа вплавь возможна на спокойной реке и для умеющих хорошо держаться на воде. Удобным местом для нее служат глубокие участки с пологим падением русла. Заранее рассчитывая на снос вниз по реке, туристы плывут под углом к течению. Не следует стремиться пересечь преграду по кратчайшей прямой,

Вещи рекомендуется сложить на легкий плот и толкать его по воде перед собой.

В некоторых случаях первый турист переправляется вплавь с охранением веревкой. Затем она используется для перетаскивания плота и помощи другим участникам группы, которые могут страховаться, придерживаясь на воде за любой нетонущий предмет— бревно, доску, вязанку хвороста или надежно упакованный в непромокаемый материал и плотно перевязанный рюкзак.

Рассмотрим два множества 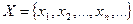и 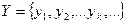. Правило, позволяющее каждому элементу 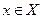поставить в соответствие единственный элемент 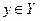, называется функцией одной переменной 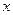и обозначается символом 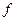. При этом элементы 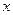множества 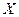называют аргументами, а само множество 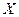называют областью определения функции 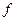и обозначают символом 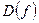. Тот элемент 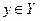, который соответствует элементу 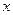, называют образом элемента 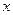, или значением функции и обозначают символом 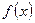, а сам элемент 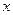называют прообразом элемента 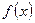. Множество всех образов элементов множества 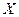называют множеством значений функции 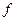и обозначают символом .

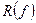Графиком функции 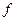с областью определения 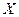называют множество точек плоскости с координатами 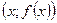, где 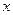пробегает всю область определения .

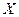Основными способами задания функций являются аналитический, графический и табличный. Аналитическим способом называют задание функции 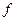формулой вида 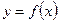. Графический способ задания функции 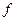состоит в задании функции ее графиком. Если же функция 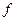задана таблицей вида

			…
			…

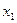
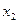
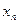
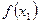
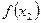
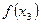
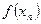
то говорят, что функция задана табличным способом.

Пусть имеем функцию 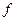с областью определения 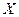и множеством значений 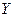. Если любые два различные значения 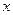имеют различные образы, то появляется возможность установить обратное соответствие между множествам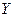и и 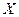так, чтобы каждому значению 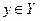сопоставлялся единственный 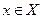, тот самый, для которого рассматриваемый 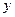являлся образом 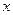функции 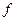. Это обратное соответствие называют обратной функцией для функции 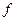и обозначают символом 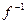. Очевидно, что если функция 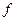с областью определения 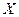и множеством значений 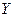имеет обратную, то для функции 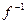множество 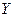будет областью определения, а множество 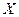множеством значений.

Рассмотрим теперь три множества 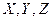. Допустим, что каждому значению 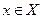функция 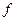сопоставляет единственное значение 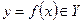, а каждому значению 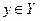функция 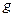сопоставляет единственное значение 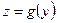. Тогда с помощью функци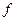й и 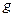каждому значению 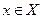можно поставить в соответствие единственный элемент 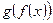множества 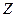. Это соответствие называют сложной функцией (или суперпозицией) с областью определения 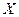и обозначают символом .

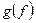Функция 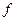, определенная на множестве 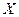, называется ограниченной сверху (снизу) если множество значений этой функции ограничено сверху (снизу), т.е. .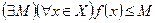

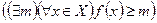Функция 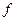называется монотонно возрастающей (убывающей) на множестве 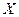, если .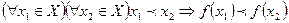

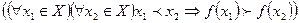Монотонность функции 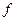является достаточным условием существования обратной функции .

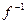Множество 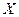называют симметричным, если вместе с любым своим элементом 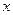оно содержит и противоположный элемент 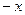. Функция 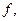определенная на симметричном множестве 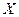, называется четной (нечетной), если .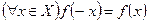

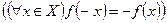Функцию 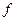, определенную на множестве 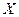, называют периодической, если . Число 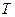при этом называют периодом функции.

Нетрудно доказать, что если функция 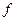периодическая и 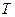- ее период, то числа 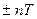, где 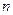- натуральное число, также являются периодами функции 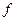. Наименьший положительный период называют основным периодом.

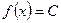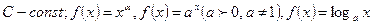
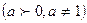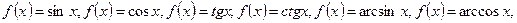
Функции , где , 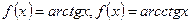называют основными элементарными функциями. Элементарной называют функцию, аналитическое выражение которой содержит лишь конечное число арифметических операций и конечное число суперпозиций основных элементарных функций.

Дата добавления: 2013-12-13