Аналоговые системы управления положением

Функциональная схема аналоговой системы управления положением приведена на рис. 2,1. В ней используется тиристорный электропривод постоянного, тока с трехконтурной

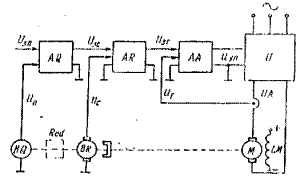
^{Рис. 2.1. Функциональная схема аналоговой системы управлением положением.}

системой управления, построенной по принципу подчиненного регулирования скорости; и тока с контурами тока, скорости и положения. Сигнал задания положения U_зп подается на регулятор положения AQ, на который также с датчика положения BQ подается сигнал обратной связи по положекию U_п. Внутренние контуры скорости и тока выполнены как, в системах стабилизации скорости [4]. В таких системах управления позиционного электропривода в качестве датчиков перемещения обычно используются датчики углового перемещения в виде сельсинов или поворотных трансформаторов, валы которых соединяются как с валом двигателя, так и с валом ИОРМ непосредственно или через редукторы (рис. 2.2). Для преобразования сигнала управления переменного тока определенной фазы, идущего с сельсина или поворотногo трансформатора

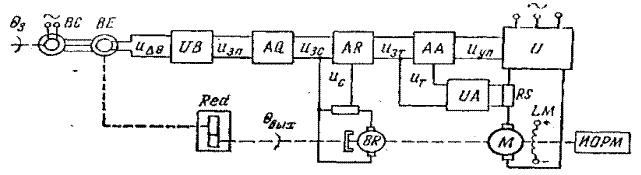
_{Рис. 2.2. Упрощенная принципиальная схема аналоговой системы управления.}

в сигнал управления постоянного тока определенной полярности в схеме используются фазочувствительные выпрямители (ФЧВ) UB. Задание положения обеспечивается задатчиком. (сельсином-датчиком ВС), который поворачивается на требуемый заданный угол θ₃,-определяющий требуемое перемещение ИОРМ. Текущее положение ИОРМ контролируется датчиком положению, который называется сельсином-приемником BE, Задачей рассматриваемой системы управления является точная остановка двигателя и соответственно ИОРМ в заданном положении. Это произойдет, когда двигатель или ИОРМ отработает заданный угол θ₃ и угол сельсина приемника BE станет равным углу задания (θ_п= θ₃), а рассогласование будет равно нулю (θ_п - θ₃=∆θ=0).

Для осуществления точной остановки в заданном положении требуется оптимизировать контур регулирования положения методом последовательной коррекции и найти передаточную функцию регулятора положения.

Для оптимизации системы составляется ее структурная схема (рис. 2.3). Поскольку внутренние контуры скорости и тока рассматриваемой системы настроены на техничес оптимум, то структурную схему можно упростить, изображая внутренние контуры одним звеном оптимизированного контура скорости с учетом контура тока с передаточной функцией следующего вида:

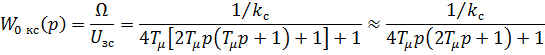
^{Рис. 2.3. Упрощенная структурная схема аналоговой системы управления положением.}

При оптимизации контура положения учитывают, что точность остановки ИОРМ в заданном положении зависит от его перемещения. Различают три вида перемещения: малое среднее и большое. При малом перемещении скорость двигателя не успевает достигать установившейся, скорости, а ток значения тока ограничения (рис. 2.4, а). В этом случае

^{Рис. 2.4. Графини скорости, и тока двигателя при различных перемещениях механизма: а —при малых; б — при средних; в — при больших}

СЭП работает как линейная. Среднее перемещение - перемещение, при котором двигатель работает по угольной тахограмме, т.е. разгоняется до установивше скорости с постоянным ускорением, а затем тормозится с постоянным замедлением. При этом (PC ограничивает ток до показателя при разбеге и торможении допустимым значением тока стопорения I_ст (рис. 2.4,6). При больших перемещениях двигатель работает по трапецеидальной тахограмме скорости, т.е. обеспечивает движение с установившейся скоростью ω_уст, определяемой ограничением U_{ЗС огр}, создаваемым РП. Ток при этом ограничен при pазбеге и торможении (рис. 2.4,в).

Настроим контур положения при малом перемещении как в линейной системе на технический оптимум. Записывая передаточную функцию разомкнутого оптимизированного контyра положения

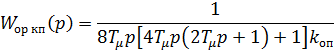
(2.2)

и передаточную функцию объекта управления

(2.3)

получим передаточную функцию регулятора положения

(2.4)

Как видно, регулятор положения получается пропорциональным. Передаточную функцию РП можно также получить по формуле n-гo регулятора [4] при n = 3 и W_к(p)^,= 1/p:

Тогда передаточная функция оптимизированного замкнутого контура положения имеет вид

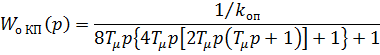
(2.5)

Согласно теории оптимизации трехконтурной системы подчиненного регулирования, переходный процесс имеет вид кривой с перерегулированием σ=6,2% и временем переходного процесса t_пп= 13,6 Т_μ. При такой настройке РП остановка двигателя и ИОРМ будет осуществляться с точностью, определяемой статической погрешностью системы 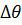_ст, вычисляемой при ω=0.

Учитывая, что в системе с подчиненным регулированием координат

(2.6)

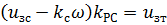
И прт регуляторе тока

(2.7)

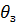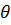определяем статическую погрешность СУ позиционного электропривода при ω=0, когда двигатель остановился. Тогда при =k_оп где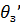— заданный угол перемещения, на ва лу сельсина-приемника, имеем

(2.8)

откуда найдем статическую погрешность позиционирования

(2.9)

Подставляя значение k_РП из (2.4) и 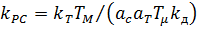[4| и учитывая, что l_с—k_дМ_с, -получим в общем виде

(2.10)

При настройке всех контуров системы на технический оптимум, когда a_п =a_c = a_T=2, статическая погрешность равна

(2.11)

где J — момент инерции электропривода.

Таким образом, из (2.11) видно, что статическая погрешность позиционирования в линейной системе определяется значениями статического момента и момента инерции электропривода. Если момент М_с большой, то статическая погрешность может оказаться значительной и по якорю неподвижного двигателя будет протекать болшгой ток I_с.

Однако режим малых перемещений для большинства paбочих машин не характерен и регулятор положения, принятый с коэффициентом k_РП согласно (2.4) не сможет обеспечить требуемую точность позиционирования при средних и больших перемещениях. Наиболее характерным считается треугольный график скорости (рис. 2.4,6) при средних перемещениях, при котором наиболее полно используется двигатель и обеспечивается быстрая (с минимальным временем) отработка заданного перемещения без дотягивания и перерегулирования скорости. Для многих производственных механизмов перерегулирование недопустимо из-за возникновения ударов в кинематических цепях передающего устройства при наличии зазоров в передачах.

Задачей настройки контура положения при средних перемещениях является выбор k_РП с учетом того, что при пуске и торможении PC ограничивает и_зг = и_{3Т огр} и, следовательно, ток двигателя значением тока стопорения. Рассмотрим работу СУ позиционного электропривода в этом режиме (рис. 2.5, а). Задание на вдод системы 0₃ в момент времени t₀ определяет

^{Рис. 2.5. Настройка контура положение при различных перемещениях механизма: а — при средних; б — при малых; в —три больших; г — фазовые траектории движения}

заданное перемещение; если θ_з велико, то при θ_вых=0 возникает большое задающее воздействие и выходной сигнал РП, являющийся сигналом задания скорости, ограничен значением U_{рп огр} = U _{3C огр}. В этом случае PC также ограничивает свой сигнал (сигнал задания тока U_{3T огр}), что ограничивает ток двигателя допустимым значением I_ст. Если M_c=const, то происходит разбег двигателя с постоянным ускорением

(2.12)

При этом отрабатывается угол θ_вых и повышается сигнал обратной связи по положению θ_п=k_оп θ_вых.

Будем считать, что при времени t=t₁ угол перемещения равен θ_вых = θ₁ и сигнал на выходе РП имеет вид

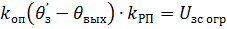
(2.13)

При этом РП выйдет из ограничения и с дальнейшие ростом скорости u_зс будет снижаться. Однако темп разбег двигателя пока не изменится, поскольку PC остается в режиме ограничения, вследствие чего ограничивается u_3T= = U_{зт огр} и ток двигателя (i=I_Ст) При дальнейшем рост ω и θ_вых наступит момент (при t=t₂)_} когда ω=ω₂, а θ_Вых= θ_Вых2, следовательно:

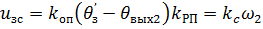
(2.14)

т.е. сигнал равен и_зс при При дальнейшее росте окажется, что и сигнал и₃ на выходе РП станет отрицательным. При этом, как и сигнал задания тока и_зт, ток двигателя изменит направление и наступит режим торможения с замедлением,

(2.15)

В этом! случае PC также ограничивает u_3T= = U_{зт огр} и ток i=I_Ст. Торможение закончится при t=t_з, когда рассогласование по положению будет равно нулю , и двигатель остановится.

Коэффициент усиления регулятора положения может быть найден из условия, что максимальная рабочая скорость при позиционировании была равна номинальной скорости электропривода ω₂ = ω_{Р ном} и при торможении с постоянным максимальным замедлением ε_T=ε_{T max}=const рассогласование по положению равно

(2.16)

Тогда подставляя в (2.14) значения 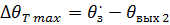из (2.16) и ω₂ = ω_{Р ном}, получим коэффициент усиления РП при среднем идеальном перемещении по треугольной тахограмме скорости

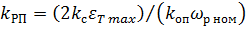
(2.17)

где .

При такой настройте РП отра-ботка заданного перемещения с треугольным графиком скорости происходит без перерегулирования и дотягивания скорости.

При других значениях заданного перемещения меньших или больших настроечного , при котором был выбран k_РП согласно (2.17), график скорости отличается от треугольного. Если скорость в начале торможения окажется меньше ω_{р ном} (рис. 2.5,6). В этом случае разгон электропривода происходит до скорости ω₂<ω_{Р ном}. Во время разгона от t ₀ до t₂ законы изменения ω и u_РП остаются такими же, как на рис. 2.5, а, так как они определяются ускорением электропривода (2.12), а равенство (2.14) достигается при меньшей скорости (ω₂ = ω_{р ном}). В процессе торможения PC ограничен до достижения скорости ω _з ', соответствующей времени t ₃', а потом PC выйдет из ограничения. Далее тормозной ток снижается., в результате чего темп торможения уменьшается и происходит так называемое дотягивание скорости на интервале времени от t₃' до t₄.

При 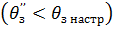разгон двигателя происходит до скорости (ω₂’’ > ω_{р ном}) (рис. 2.5, в); так как при скорости ω₂ рассогласование 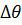еще достаточно велико, то РП не вывдет из режима ограничения u_3С= = U_{зс огр}. Поэтому возникает установившийся процесс движения и график скорости будет трапецеидальным. Торможение при отработке начинается с большей скорости ω₂’’, а процесс снижения скорости будет.происходить с перерегулированием, потому что при отработке двигатель еще будет вращаться со скоростью ω₃’’, при которой PC не выйдет из режима ограничения и будет существовать тормозной момент.

Работа линейного регулятора положения xоpoшо видна при изображении фазовьгх траекторий движения НОРМ на фазовой плоскости при угловом 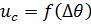или линейном перемещениях (рис. 2.5, г), где u_c=k_cω — сигнал обратной связи по скорости, пропорциональный скорости. При иастройке регулятора по среднему перемещению, когда 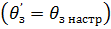(кривая 3), скорость двигателя изменяется ^;при позиционировании без перерегулирования и дотягивания. При меньших перемещениях скорость изменяется с дотягиванием (кривые 1 и 2), а при больших — с перерегулированием (кривые 4, 5, 6).

Для того чтобы процесс торможения при остановке для любых θ₃ происходил с постоянным ускорением без дотягивания и перерегулирования до ω = 0, регулятор положения должен иметь нелинейную характеристику, как видно из (2.17), при которой k_РП менялся бы обратно пропорциональ-шо скорости ω. Такая характеристика получается, если продифференцировать (2.14) при ω ₂ = ω _т и текущих значениях перемещения θ₂ = θ

Откуда при и при получим

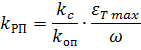
(2.18)

Учитывая, что при любом перемещении 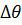и скорости ω зависимость (2.16) сохраняется, определим начальную скорость торможения

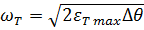
(2.19)

и, подставляя (2.19) в (2.18), получим коэффициент усиления регулятора положения

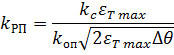
(2.20)

Такой регулятор назвали параболическим. Зависимость вы­ходного итапряжения от ДО параболического РП согласно (2.14) и (2.20) имеет вид

(2.21)

где .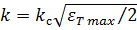

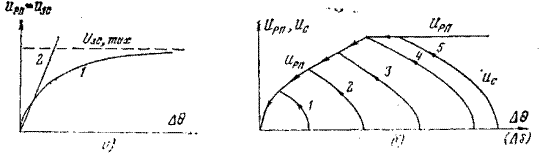
^{Рис. 2.6. Параболический регулятор положения: a — характеристика; б — фазовые траектории движения.}

Зависимость u_vn(∆ θ ) параболического РП показана на рис. 2.6, а (кривая 1). Однако такой параболический РП имеет недостаток, связанный с тем, что при ∆ θ → 0 k_РП возрастает и теоретически 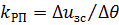стремится к бесконечности. Это может вызывать колебания и неустановившийся процесс изменения скорости. В соответствии с этим k_РП в начале характеристики РП при ограничивают допустимым значением и начальный участок характеристики делают линейным, соответствующим настройке РП согласно (2.4) оптимизации контура на технический оптимум (прямая 2). Из рассмотрения фазовых траекторий движения u_c=f( 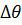) (рис. 2.6,б) видно, что любое заданное положение (кривые 1 —5) отрабатывается без дотягивания и перерегулирования.

Дата добавления: 2013-12-13