Графический метод определения передаточного числа. Построение плана скоростей

Кинематика планетарных передач.

Для передачи вращения, момента и мощности, от одного основного звена планетарной передачи, изображенной на рисунке 30 к другому надо или затормозить третье звено или сообщить ему принудительное вращение.

В самом деле, пусть ведущим элементом планетарной передачи будет солнечная шестерня, а ведомым – водило, тогда при свободном эпицикле водило, нагруженное внешним сопротивлением, останется неподвижным, а эпицикл будет вращаться вхолостую. Так будет и в любом другом случае, когда одно из основных звеньев свободно. Во всех этих случаях передать мощность через планетарную передачу нельзя, так как её элементы не имеют силовых связей между собой. Чтобы передать вращение от солнечной шестерни к водилу, надо остановить эпицикл или задать ему определенное принудительное вращение.

Планом линейных скоростей планетарной передачи называется система векторов скоростей звеньев, расположенных в совмещенной плоскости вращения всех колес, построенных в одном масштабе. Начало каждого вектора лежит на одной линии, пересекающей центральную ось и ось одного из сателлитов в каждом планетарном ряду.

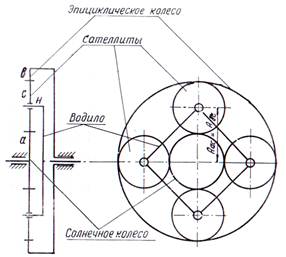
Рис. 30

План скоростей наглядно показывает соотношение величин скоростей звеньев планетарной передачи, направление их вращения, величину передаточного числа, относительные скорости в полюсах зацепления, которые определяют потери мощности на трение в этих полюсах.

При построении плана скоростей определяется окружная скорость какого-либо основного звена по заданному числу оборотов, например:

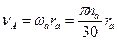
и наносится в масштабе на план скоростей, рис 31. В центре вращения (точка О) линейная скорость равна нулю. Прямая 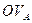ограничивает линейные скорости любой точки солнечной шестерни, лежащей в сечении ОА, а отношение этих скоростей к их радиусам определяют угловую скорость солнечной шестерни:

.

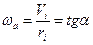Линейная скорость в точке Б, которая является мгновенным центром вращения, равна нулю, так как эпицикл остановлен. Прямая 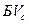определяет линейные скорости всех точек сателлита в сечении БА, так как скорости в полюсах А и Б являются не только скоростями солнечной шестерни и эпицикла, но и точек сателлита, находящихся в контакте с этими колесами. Значит, известна скорость центра сателлита, которая является и линейкой скоростью водила в точке В. Прямая 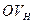, определяет линейные скорости всех точек водила, лежащих на прямой ОВ, отношение этих скоростей к их радиусам определяет угловую скорость водила:

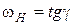
Рис. 31

Передаточное число:

.

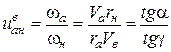Проведя вспомогательную линию 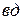на любом расстоянии от точки О, передаточное число равно отношению отрезков прямой, лежащей между линией нулевой скорости ОВ и прямым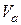и и 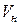. Так как

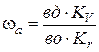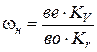и , то

.

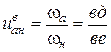Методом графического анализа кинематики планетарных передач можно определить передаточное отношение u для любых условий работы планетарного ряда. (Рис. 32). Этот метод прост и нагляден, однако недостаточно точен.

Рис. 32

Дата добавления: 2013-12-13