Методы кодирования

На рисунке 1 представлен вариант классификации методов сжатия, основанный на принципе «с потерями видеоинформации/без потерь».

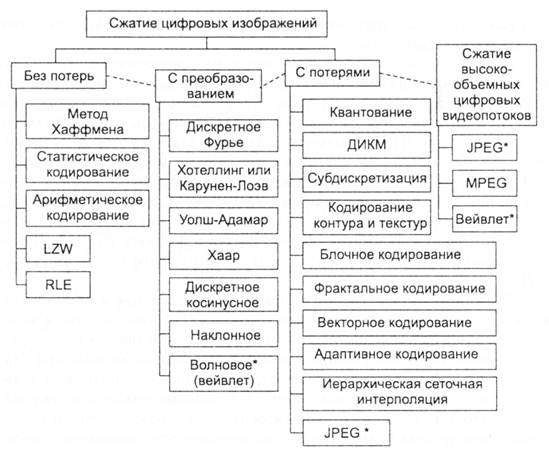
Рисунок 1 - Классификация методов сжатия (* вейвлет и JPEG в двух классах)

Сжатие данных без потерь (Lossless data compression) — метод сжатия данных, при использовании которого закодированные данные могут быть восстановлены с точностью до бита. При этом оригинальные данные полностью восстанавливаются из сжатого состояния. Для каждого из типов цифровой информации, как правило, существуют свои оптимальные алгоритмы сжатия без потерь.

Сжатие данных без потерь используется во многих приложениях. Например, оно используется во всех файловых архиваторах. Оно также используется как компонент в сжатии с потерями.

Недостатком методов сжатия без потерь является сравнительно небольшой коэффициент сжатия – до 5:1.

Другая группа методов сжатия – методы сжатия видеоданных с потерями информации (Lossy compression). Смыслэтого термина состоит в том, что после декодирования данные отличаются от исходных, но степень отличия не является существенной с точки зрения их дальнейшего использования. Например, распределение яркости в восстановленном изображении отличается от того распределения, которое было до его кодирования, т.е. имеет место искажение изображения и соответственно потеря информации. Но зачастую речь идет о той информации, которую зрительная система не в состоянии воспринять в силу присущих ей ограничений.

Коэффициент сжатия данных, который обеспечивают эти методы, может достигать 50:1.

Дискретное косинусное преобразование

Внутрикадровое сокращение избыточной информации основано на дискретном косинусном преобразовании (ДКП), который базируется на преобразовании, предложенном французским математиком Ж. Фурье. Согласно нему, любую периодическую последовательность импуль­сов можно представить в виде алгебраической суммы простейших синусоидальных колебаний с кратным частотами и убывающими ам­плитудами. Точное приближение к исходной форме импульса дает практически всегда бесконечный ряд частот, кратных основной.

Совокупность целого ряда убывающих колебаний разных частот об­разует спектр исходного (в данном случае прямоугольного) импульса.

Передать все составляющие его колебания не просто, так как для этого требуется очень широкая частотная полоса канала связи. И чем короче импульс, т. е. чем мельче деталь изображения, тем более ши­рокой необходима частотная полоса. При недостаточной ширине полосы фазы колебаний с высшими частотами (гармоники) будут изменяться, и колебания будут ослабляться по амплитуде, что приведет к потере качества изображения.

Пиксель как сигнал можно анализировать, если перевести его из амплитудно-временного представления в амплитудно-частотное, т. е. получить его частотный спектр. В спектре наглядно видны колебания, расположенные в низкочастотной области, несущие основную энер­гию и формирующие амплитуду импульса-пикселя, а также колебания менее значимые, находящиеся в высокочастотной области спектра, формирующие крутизну фронта и спада, определяющие ширину час­тотной полосы, занимаемую пикселем (рис. 2).

Рисунок 2 - Частотный спектр пикселя - элемента яркости

В большинстве случаев колебания в крайне правой высокочастот­ной области спектра значительной роли для пикселя, как составляю­щего элемента видеосигнала, не имеют. То есть передаются только те коэффициенты, которые превышают пороговую величину, а ос­тальные считаются нулевыми. Введение порога, строго говоря, при­водит к потерям информации и, соответственно, к снижению качества изображения, однако при оптимальном выборе величины порога та­кое ухудшение окажется практически незаметным.

На рис. 2 выделены колебания с менее значимыми частотами и амплитудами, которые можно удалить, что приведет к некоторому снижению четкости и контрастности видеоизображения, с одной сто­роны, но с другой, даст возможность: значительно сузить частотную полосу, занимаемую видеосигналом и уменьшить необходимый объ­ем памяти для запоминания значений оставшихся амплитуд и частот.

На этом построено уменьшение видеоинформации при внутрикадровом сжатии цифровых данных на основе ДКП.

Дата добавления: 2013-12-13