Правила дифференцирования

Задача о проведении касательной к кривой

Производная. Дифференциал функции

Примеры.

1)

2) .

3) Проверить непрерывность функции .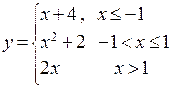

Поскольку функци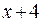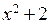и , и 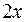непрерывны в областях их задания, достаточно рассмотреть функцию 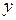в точках стыковки этих функций. Итак, для 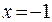имеем , , .

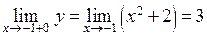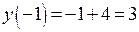Функция в этой точке непрерывна согласно определению 4.

Для имеем 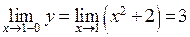, , 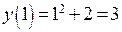. Условие непрерывности в точке не выполняется.

Следовательно, функция 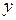непрерывна на всей числовой оси за исключением точки , где она имеет конечный разрыв со скачком

(-1).

Пусть заданная кривая является графиком непрерывной функции 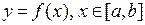, и требуется провести касательную к этой кривой в точке 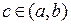. Заметим, что касательная – это прямая, получающаяся в пределе из хорд, проходящих через точки 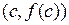и , когда 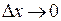. Уравнение хорды – прямой, проходящей через две заданные различные точки, – имеет вид: 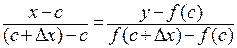или 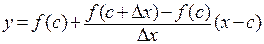. Делая предельный переход при 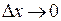, получим предельное значение углового коэффициента хорд – угловой коэффициент касательной: . На рисунке касательная представлена пунктиром. Итак, , где – угол, образованный касательной с положительным направлением оси .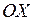

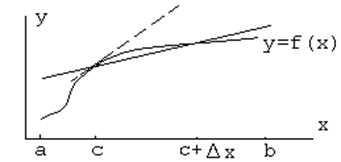
Очевидно, что существуют непрерывные кривые, в некоторых точках которых провести касательную невозможно.

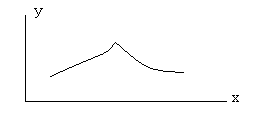
Возникает вопрос: какое условие нужно наложить на функцию 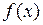в окрестности точки 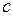, чтобы в соответствующей точке можно было провести касательную к графику этой функции.

Определение 1. Функция 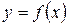называется дифференцируемой в точке 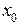, если ее приращение 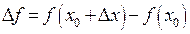представимо в виде 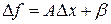, причем 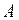– константа, 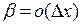– бесконечно малая функция, более высокого порядка малости, чем , то есть .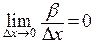

Установим значение , для чего вычислим

.

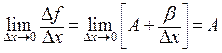Назовем число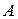 производной функции в точке 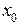и обозначим ее 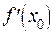, в результате получаем определение производной 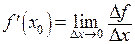и, кроме того,

.

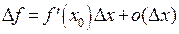Как было сказано выше, второе слагаемое в выражении приращения функции – величина более высокого порядка малости, чем величина , а следовательно, и чем величина 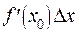. Другими словами, первое слагаемое в выражении приращения функции представляет основную часть приращения функции. Называют его дифференциалом функции в точке 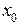и обозначают 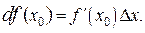В целях единообразия и для того, чтобы подчеркнуть, что – бесконечно малая величина, приращение аргумента в этой формуле обозначают 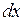. Тогда 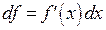, откуда следует второе обозначение производной . Связь между приращением функции и ее дифференциалом изображена на рисунке 1.

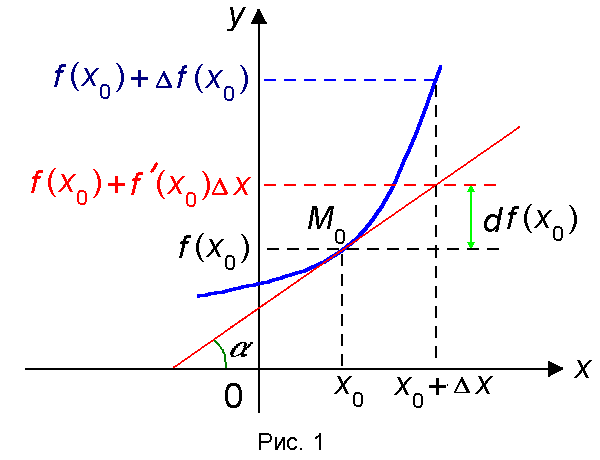
Замечание. Геометрическим смыслом производной 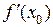является тангенс угла наклона касательной к кривой 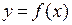в точке 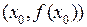. Поэтому уравнение касательной к кривой 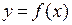в точке 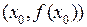имеет вид .

Физическим смыслом производной 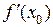является скорость в момент , когда зависимость длины пути 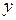от скорости задается функцией .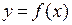

1) Производная суммы функций есть сумма производных этих функций.

Пусть 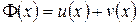, тогда

.

Очевидно, .

2) .

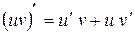3) .

Свойства 2) и 3) доказываются аналогично свойству 1).

4) Пусть функция 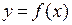дифференцируема в точке 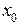, 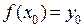. Пусть функция дифференцируема в точке 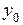. Тогда сложная функция дифференцируема в точке 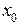, причем .

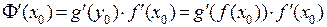Действительно,

.

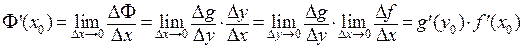Дата добавления: 2013-12-13