Физический смысл производной. Мгновенная скорость изменения функции, ускорение и градиент

Таблица 2

Таблица 1

Понятие предела переменной. Производная функции. Таблица производных. Правила дифференцирования

Способы задания функций. Виды элементарных функций

Задать функцию - значит задать правило или закон, согласно которому данному значению аргумента х определяется соответствующее значение функции у.

Рассмотрим способы задания функции.

1. Аналитический способ - задание функции с помощью формул. Например, растворение лекарственных веществ из таблеток при приготовлении растворов подчиняется уравнению m = m₀е^–kt, где m₀ и m – соответственно,исходное и оставшееся ко времени растворения t количество лекарственного вещества в таблетке, k – некоторая постоянная положительная величина.

2. Графический способ - это задание функции в виде графика. Например, с помощью электрокардиографа на бумаге или на экране монитора компьютера фиксируется возникающая при работе сердца величина разности биопотенциалов U как функция времени t: U = f(t).

3. Табличный способ - это задание функции с помощью таблицы. Такой способ задания функции используется в экспериментах и наблюдениях. Например, измеряя температуру тела больного через определенные промежутки времени, можно составить таблицу значений температуры тела Т как функции времени t. На основании табличных данных иногда оказывается возможным выразить приближенно формулой соответствие между аргументом и функцией. Такие формулы называют эмпирическими, т.е. полученными из опыта.

В математике различают элементарные и сложные функции. Приведем основные виды элементарных функций:

1. Степенная функция – y = f(x) = xⁿ, где х – аргумент, n – любое действительное число (1, 2, - 2, 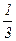и т.д.).

2. Показательная функция – y = f(x) = a^x, где а - постоянное положительное число, отличное от единицы (а > 0, а ≠ 0), например:

y = 10^x (a = 10);

y = e^x; y = e^-x (a = e ≈ 2,718…)

Выделим две последние функции, они называются экспоненциальными функциями или экспонентами и описывают множество физических, биофизических, химических и социальных процессов. Причем y = e^x – возрастающая экспонента, y = e^-x – убывающая экспонента.

3.Логарифмическая функция с любым основанием а: y = log_ax, где у - степень, в которую нужно возвести основание функции а, чтобы получить данное число x, т. е. a ^y = x.

Если основание а = 10, то y называется десятичным логарифмом числа x и обозначается y = lg x; если a=e, то y называется натуральным логарифмом числа x и обозначается у =1n х.

Напомним некоторые правила логарифмирования:

Пусть даны два числа а и b, тогда:

· lg (a·b) = lg a + lg b;

· lg 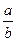= lg a - lg b;

· lg ab = b lg a;

Ничего не изменится при замене символа lg на ln.

Полезно также помнить, что lg 10 = 1, ln е = 1, lg 1 = ln 1 = 0.

4. Тригонометрические функции: y = sin x, y = cos x, y = tg x и др.

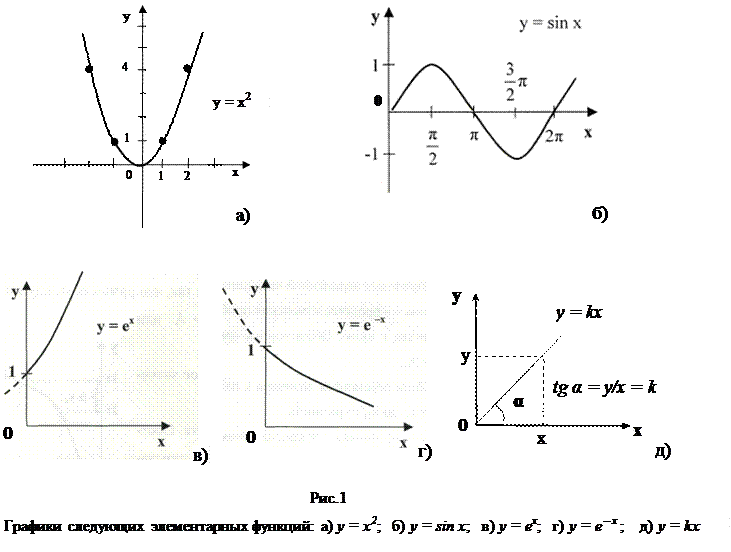Приведем графики некоторых элементарных функций (см. рис. 1):

Переменная величина может изменяться так, что в процессе возрастания или убывания она приближается к некоторой конечной постоянной величине, которая является ее пределом.

По определению пределом переменной величины х называется постоянная величина А, к которой переменная х в процессе своего изменения приближается так, что модуль разности между x и А, т.е. | х - А |, стремится к нулю.

Обозначения предела: x→ А или lim x = A (здесь → - знак предельного перехода, lim от лат. limited, в переводе на русский – предел). Рассмотрим элементарный пример:

x: 0,9; 0,99; 0,999; 0,9999…→ 1, A = 1(lim x = 1), т.к.

| х - А |: 0,1; 0,01; 0,001; 0,0001…→ 0.

Введем понятия приращение аргумента и приращение функции.

Если переменная величина х изменяет свое значение от x₁ до х₂, то разность x₂ – x₁ = Δx называется приращением аргумента, причем Δx (читается дельта х) – единый символ приращения. Соответствующее изменение функции y₂ – y₁ = Δy называется приращением функции. Покажем это на графике функции y = f(x) (рис. 2). Геометрически приращение аргумента изображается приращением абсциссы точки кривой, а приращение функции - приращением ординаты этой точки.

Производной заданной функции y = f(x) по аргументу х называется предел отношения приращения функции Δу к приращению аргумента Δх, когда последнее стремится к нулю (Δх → 0).

Производная функции обозначается (читается «у штрих») или , или dy/dx (читается «дэ y по дэ x»). Таким образом, производная функции y = f(x) равна:

(4)

Правило для отыскания производной функции у = f(х) по аргументу х содержится в определении этой величины: нужно задать приращение аргумента Δх, найти приращение функции Δy, составить отношение и найти предел этого отношения при Δх→ 0.

Процесс нахождения производной называется дифференцированием функции. Этим занимается раздел высшей математики называемый «Дифференциальное исчисление».

Таблица производных основных элементарных функций, полученных по указанному выше правилу, приведена ниже.

№ п/п	Виды функции	Производная функции
	Постоянная величина y = c	y' = 0
	Степенная функция y = x^n (n может быть положительным, отрицательным, целым, дробным)	y' = nx^n-1
	Показательная функция y = a^x (a > 0; a ≠ 1) y = e^x y = e^-x, у=e^-kx (k=const)	y' = a^xln a y' = e^x y' = - e^-x, y' = -k e^-kx
	Логарифмическая функция y = logax (a > 0; a ≠ 1) y = ln x	y' = y' =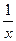
	Тригонометрические функции: y = sin x y = cos x y = tg x y = ctg x	y' = cos x y' = - sin x y' = y' =

Если выражение, производную которого надо найти, представляет собой сумму, разность, произведение или частное нескольких функций, например, u, v, z, то используются нижеприведенные правила дифференцирования (табл. 2).

1. y = u + v – z	1) y' = u' + v ' - z'
2. y = u · v	2) y = u' · v + v '· u
3. y =	3) y' =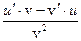
4. y = a · u, где a = const	4) y' = a · u'

Приведем несколько примеров вычисления производных, используя таблицы 1 и 2.

1. (x + sin x)' = (x)' + (sin x)' = 1 + cos x;

2. (x · sin x)' = (x)' · sin x + x · (sin x)' = sin x + x cos x;

3. ;

4. (5 tgx)' = 5 (tg x)' = .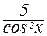

Физический смысл производной состоит в том, что она определяет быстрота (темп) изменения функции.

Рассмотрим пример прямолинейного движения. Скорость тела равна отношению пути ΔS, пройденного телом за время Δt, к этому промежутку времени v = 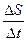. Если движение неравномерное, то отношение 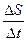является средней скоростью на этом участке пути, а скорость, соответствующая каждому данному моменту времени, называется мгновенной скоростью движения и определяется как предел отношения 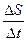при Δ t→0, т.е.

Обобщая полученный результат, можно утверждать, что производная функции f(x) по времени t является мгновенной скоростью изменения функции. Понятие мгновенной скорости относится не только к механическим движениям, но и к любым процессам, развивающимся во времени. Можно найти скорость сокращения или расслабления мышцы, скорость кристаллизации раствора, скорость отвердевания пломбировочного материала, скорость распространения эпидемического заболевания и др.

Значение мгновенного ускорения во всех этих процессах равно производной функции скорости по времени:

. (5)

В механике 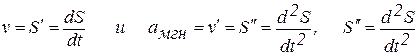— вторая производная пути по времени.

Понятие производной, как величины, характеризующей быстроту изменения функции, применяется для разных зависимостей. Например, надо узнать, как быстро изменяется температура вдоль металлического стержня, если нагревать один из его концов. В данном случае температура - функция координаты x, т.е. T = f(x) и характеризует темп изменения температуры в пространстве.

Производную некоторой функции f(x) по координате x называют градиентом этой функции (часто используется сокращение grad от лат. gradient). Градиенты различных переменных – это векторные величины, всегда направленные в сторону увеличения значения переменных.

Отметим, что градиенты многих величин являются одной из первопричин обменных процессов, происходящих в биологических системах. Это, например, градиент концентрации , градиент электрохимического потенциала 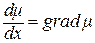(μ – греческая буква «мю»), градиент электрического потенциала .

При малых Δx можно записать:

. (6)

Дата добавления: 2013-12-13