Свойства степенных рядов

В силу теоремы Абеля степенной ряд сходится равномерно на , его можно почленно дифференцировать и интегрировать в интервале сходимости.

Теорема. Сумма степенного ряда – это функция, имеющая внутри интервала сходимости производные любого порядка. Эти производные являются суммами степенных рядов, полученных из данного функционального ряда почленным дифференцированием его элементов соответствующее число раз, причем радиус сходимости каждого «производного» ряда тот же, что и у исходного функционального ряда.

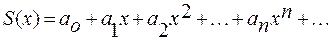
Теорема. Сумма степенного ряда есть функция аналитическая в интервале сходимости.

Можно выразить коэффициенты степенного ряда через производные от функции суммы данного ряда

Таким образом, коэффициенты степенного ряда являются соответствующими коэффициентами Тейлора для функции в точке .

Если имеется некоторая функция можно ли ее представить в виде суммы некоторого степенного ряда или, другими словами, можно ли данную функцию разложить в степенной ряд.

Разложение функций в степенные ряды.

Определение. Функцию можно разложить в степенной ряд по степеням разности 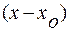, то этот ряд обязательно является рядом Тейлора этой функции.

,

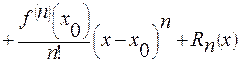где 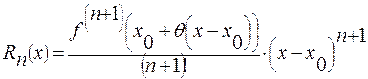- остаточный член в форме Лагранжа, где .

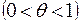Необходимым условием разложения функции в ряд Тейлора является дифференцируемость функции бесконечное число раз.

Для того, чтобы ряд Тейлора сходился к данной функции , абсолютные величины всех производных функции должны быть ограничены одним и тем же числом , где - постоянная не зависящая от 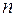. Остаточный член определяется неравенством .

Разложение элементарных функций в степенные ряды.

1.

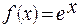
на любом интервале оси 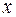, значит для всех .

(1)

2.

,

……………………………………………

.

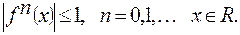
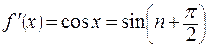
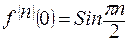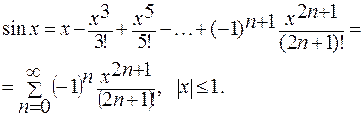
3.

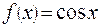
4.

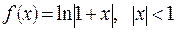
Продифференцируем и разложим производную по формуле суммы бесконечно убывающей геометрической прогрессии:

Продифференцируем это равенство почленно:

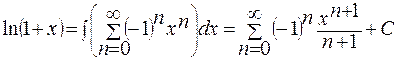постоянную интегрирования найдем, полагая .

.

5.

Представим функцию арктангенса в виде интеграла с переменным верхним пределом 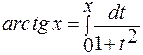. По формуле суммы бесконечно убывающей геометрической прогрессии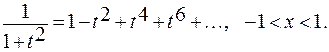

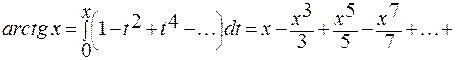
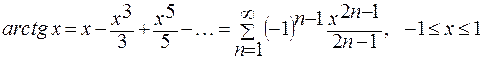
7. - производное постоянное число.

,

,

,

………………………………………………………………………

,

.

.

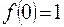
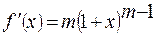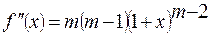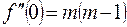
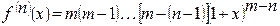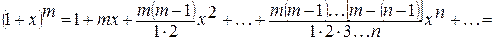
Область сходимости этого ряда находится по признаку Даламбера:

.

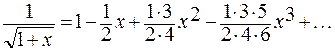
Дата добавления: 2013-12-13