
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Конспект лекции
|
|
|
|
Кафедра уголовного процесса
Способы графического задания прямой линии
Прямая линия
Прямая линия- одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, вдоль которой расстояние между двумя точками является кратчайшим.
Прямая линия - алгебраическая линия первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением 1 - ой степени (линейное уравнение).
Общее уравнение прямой (полное):
Ах+Ву+С=0,
где А, В и С - любые постоянные, причем А и В одновременно не равны нулю. Если один из коэффициентов равен нулю, уравнение называется неполным.
Для определения положения прямой в пространстве существуют следующие методы:
1. Двумя точками (А и В).
Рассмотрим две точки в пространстве А и В (рис. 15). Через эти точки можно провести прямую линию. Для того чтобы найти проекции отрезка [AB] на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка:
[A1B1]<[AB]; [A2B2]<[AB]; [A3B3]<[AB].
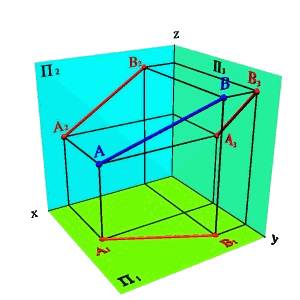
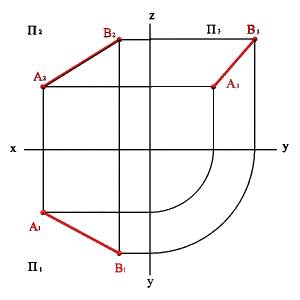
а) модель б) эпюр
Рисунок 15.Определение положения прямой по двум точкам
Обозначим углы между прямой и плоскостями проекций через α- с плоскостью П1, β- с плоскостью П2, γ- с плоскостью П3 и тогда получим:
|А1В1|=|AB|cos a
|A2B2|=|AB|cos b
|A3B3|=|AB|cos g.
Частный случай |A1B1|=|A2B2|=|A3B3| при таком соотношении прямая образует с плоскостями проекций равные между собой углы a=b=g=350, при этом каждая из проекций расположена под углом 450 к соответствующим осям проекций.
2. Двумя плоскостями (a; b).
Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии
3. Двумя проекциями.
Пусть в плоскостях П1 и П2 даны проекции прямых заданных отрезками [А1В1] и [A2B2]. Проведем через эти прямые плоскости a и b перпендикулярные плоскостям проекций. В том случае если эти плоскости непараллельные (рис.16а), линией их пересечения будет прямая заданная отрезком [АВ], проекциями которой являются отрезки [А1В1] и [А2В2].

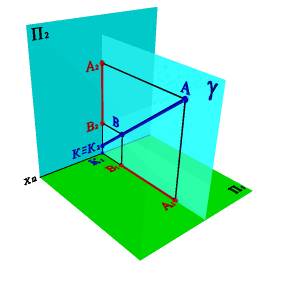
а) a непараллельная b б) a и b совпадают
Рисунок 16.Определение положения прямой в пространстве по двум проекциям отрезка
Плоскости a и b могут слиться в одну плоскость g, если, например, проекции [А1В1] и [А2В2] перпендикулярны оси x и пересекают ее в одной точке (рис.16b). Прямая линия в этом случае будет однозначно определена своими проекциями, если на каждой из них обозначить две какие-либо точки. Если же обозначений не делать, то за искомую прямую можно принять любую прямую, лежащую в этой плоскости при условии, что она непараллельная ни одной из плоскостей проекций. Точка К, в данном случае - точка пересечения прямой с плоскостью П2.
4. Точкой и углами наклона к плоскостям проекций.
Зная координаты точки принадлежащей прямой и углы наклона ее к плоскостям проекций можно найти положение прямой в пространстве(рис.17).
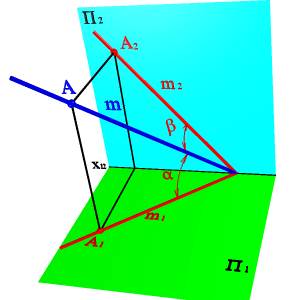
Рисунок 17. Определение положения прямой по точке и углам наклона к плоскостям проекций
Утверждаю
Начальник кафедры
уголовного процесса
подполковник полиции
Н.Г. Логинова
«___»____________2011 г.
Актуальные проблемы
применения уголовно-процессуального законодательства
По теме:
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 590; Нарушение авторских прав?; Мы поможем в написании вашей работы!