Виды проецирования

Пример.

Схема алгоритма Рабина - Миллера

Пусть дано нечетное число p. Надо проверить является ли число p простым. Далее предположим, что p - 1 = 2st.

1. Выбираем случайное число a, меньшее p и

определяем k = 0.

2. Вычисляем с помощью алгоритма Эвклида НОД двух чисел a и p. Если НОД (a, p) ¹ 1, то p – составное число.

3. Вычисляем b º at mod p. Если b = 1 или b = p - 1, то число p вероятно простое.

4. Если b¹ 1 и b ¹ p - 1, то вычисляем b º b2 mod p и k= k + 1.

5. Если число b = p - 1, то число p вероятно простое.

Перейти на шаг 7.

6. Пока k < s выполнять пункт 4.

7. Завершить работу алгоритма.

Рассмотрим примеры.

Пусть p = 181. Имеем p - 1 = 45 ´ 22. По

представленному разложению определяем значение

параметра t = 45.

1. Выбираем случайное число a = 52 < p, и

определяем k = 0.

2. Используем алгоритм Эвклида для вычисления

НОД двух чисел 52 и 181:

делим число 181 на число 52, получаем 181 = 52 ·

3 + 25;

делим число 52 на число 25, получаем 52 = 25 · 2

+ 2;

делим число 25 на число 2, получаем 25 = 12 · 2 +

1;

делим число 2 на число 1, получаем 2 = 1 · 2 + 0; получаем, что НОД двух чисел 181 и 52 равен 1.

Так как НОД не позволяет установить является ли число 181 составным, то продолжаем выполнять алгоритм Рабина - Миллера.

3. Последовательно вычисляем

b º 52t mod 181 º 5245 mod 181:

522 mod 181 º 2704 mod 181 º 170 mod 181,

524 mod 181 º 1702 mod 181 º 28900 mod 181 º

121 mod 181,

528 mod 181 º 1212 mod 181 º 14641 mod 181 º

161 mod 181,

5216 mod 181 º 1612 mod 181 º 25921 mod 181 º

38 mod 181,

5232 mod 181 º 382` mod 181 º 1444 mod 181 º

177 mod 181,

5240 mod 181 º (5232 mod 181)(528 mod 181) º

º (177 ´ 161) mod 181 º 28497 mod 181 º 80 mod

181,

5241 mod 181º (5240 mod 181)(52 mod 181) º (80 ´

52) mod 181 º

º 4160 mod 181 º 178 mod 181,

5245 mod 181 º (5241 mod 181)(524 mod 181) º (178 ´

121) mod 181 º

º 21538 mod 181 = 180 mod 181.

Итак, получили b = 180 = p - 1. Откуда следует, что

число p = 181 вероятно простое.

Замечание.

Для генерации даже небольших простых чисел вычисления довольно громоздки. Поэтому для реальных чисел, несомненно, подобные проверки

чисел на простоту надо делать при помощи программ на компьютере.

В [10] дается некоторое руководство при генерации простых чисел для практических приложений. Это руководство сводится к реализации нескольких этапов

(шагов).

1. Сгенерируйте случайное n-битовое число p.

2. Установите старший и младший биты равными 1.

Старший бит в этом случае гарантирует требуемую длину простого числа, а младший –

его нечетность.

3. Убедитесь, что число p не делится на малые простые числа 3, 5, 7, 11 и т. д. Наиболее

надежна проверка делимости на все простые числа, меньше 2000.

4. Выполните тест Рабина - Миллера для некоторого случайного числа a. Если p проходит тест, то сгенерируйте другое случайное число a и повторите тест. Для практических приложений достаточно повторить тест Рабина – Миллера пять раз.

5. Если p не проходит один из тестов, надо сгенерировать другое число p и повторить

данное руководство снова.

Другое число p, если оно оказалось не простым, можно получить не генерируя новое, а последовательно перебирая все целые, начиная от p + 1, p + 2, и т. д., пока не найдется простое число.

Перейдем теперь к вопросу о генерировании больших простых чисел.

Построение больших простых чисел и детерминированные алгоритмы проверки чисел на

Простоту/

Рассмотрим еще один способ формирования простых чисел. Этот способ базируется на определенной процедуре генерирования простых чисел, проверка которых осуществляется с помощью тестов на простоту.

Такой подход применяется, например, в стандарте

электронной цифровой подписи (ЭЦП) ГОСТ Р 34.10–94 и

основывается на следующей теореме [12].

Теорема 5.

Пусть p = qN + 1, где q – нечетное

простое число, N – четное число и p < (2q + 1)2. Число p

является простым, если выполняются два условия:

1) 2qN = 1 mod p;

2) 2N ≠ 1 mod p.

Генерация простого числа с использованием теоремы 5 осуществляется по несколько упрощенной в принятом стандарте схеме [12]. Пусть требуется

сформировать простое число p длины t ≥ 17 бит. С этой целью строится убывающая последовательность чисел {ti}, где i = 0, 1, …, s, для которых t0 = t, ti = [ti - 1/2].

Далее последовательно вырабатывается последовательность простых чисел ps, ps - 1, … p0, для всех i = 1, …, s. Генерация простого числа pi - 1 осуществляется с использованием следующее

формулы pi - 1 = piN + 1, где число N удовлетворяет следующим условиям [12]:

· N – четное;

· N – такое, что длина числа pi - 1 = piN + 1 в

точности должна быть равна ti - 1.

В стандарте ГОСТ дается некоторый алгоритм вычисления числа N. Для учебного варианта N –

случайное четное число, которое получают с помощью датчика случайных чисел (если N – нечетно, то N = N + 1).

Число pi - 1 считается полученным, если одновременно выполнены следующие два условия:

1) 2b = 1 mod pi, b = pi - 1N;

2) 2N ≠ 1 mod pi.

Если хотя бы одно из условий не выполняется, то значение числа N увеличивается на 2, и вычисляется

новое значение pi - 1, которое снова проверяется на простоту по двум условиям. Данный процесс продолжается до тех пор, пока не будет получено простое число pi - 1 (т. е. условия 1 и 2 алгоритма генерации простого числа будут выполнены).

Заметим, что с 2002 года вышеупомянутый отечественный стандарт ЭЦП заменен на новый ГОСТ Р 34.10–2001 [7].

Одно из основных геометрических понятий - отображение множеств. В начертательной геометрии каждой точке трехмерного пространства ставится в соответствие определенная точка двумерного пространства – плоскости. Геометрическими элементами отображения служат точки, линии, поверхности пространства. Геометрический объект, рассматриваемый как точечное множество отображается на плоскость по закону проецирования. Результатом такого отображения является изображение объекта.

В основу любого изображение положена операция проецирования, которая заключается в следующем. В пространстве выбирают произвольную точку S (рис.1) в качестве центра проецирования и плоскость Пi, не проходящая через точку S, в качестве плоскости проекций (картинной плоскости). Чтобы спроецировать точку А на плоскость Пi, через центр проецирования S проводят луч SА до его пересечения с плоскостью Пi в точке Аi. Точку Аi принято называть центральной проекцией точки А, а луч SА - проецирующим лучом.

Описанные построения выражают суть операции, называемой центральным проецированием точек пространства на плоскость.

В евклидовом пространстве существуют точки, которые не имеют центральных проекций, и наоборот в плоскости Пi есть точки, которые в пространстве не имеют оригиналов (точки D и F).

Точка F прямой m принадлежит плоскости Ω, проходящей через центр проецирования S и расположенной параллельно плоскости проекций, таким образом проецирующий луч SF параллелен плоскости проекций, а точка F, как и все точки лежащие в плоскости Ω не имеют центральных проекций на Пi.

Рисунок 1. Центральное проецирование

Точка Di проекции прямой mi не имеет оригинала на прямой m, так как проецирующий луч SDi параллелен прямой.

Для исключения подобных случаев евклидово пространство расширяют введением несобственных (бесконечно удаленных) точек. Такое пространство называется расширенным евклидовым пространством.

Проецирующие лучи, проведенные через все точки кривой n, образуют проецирующую коническую поверхность N (рис.2). Проекция криволинейной фигуры, таким образом, представляет собой линию пересечения проецирующей поверхности N и плоскости проекций Пi.

Рисунок 2. Центральное проецирование линии

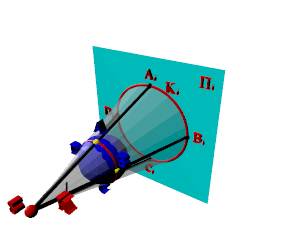
Рисунок 3. Центральное проецирование поверхности

Коническую поверхность К образуют лучи и при проецировании трехмерной фигуры (рис.3). Линию Ki принято называть в этом случая очерковой или очерком данной фигуры.

Центральное проецирование есть наиболее общий случай проецирования геометрических объектов на плоскости.

Основными и неизменными его свойствами (инвариантами) являются следующие:

1) проекция точки – точка;

2) проекция прямой – прямая;

3) если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой.

По принципу центрального проецирования работают фотоаппараты и кинокамеры. Упрощенная схема работы человеческого глаза близка к этому виду проецирования: роль центра проецирования выполняет оптический центр хрусталика, роль проецирующих прямых – лучи света; плоскостью проекций служит сетчатка глаза. Поэтому изображения, построенные по принципу центрального проецирования, наиболее наглядны и их широко используют в своей работе художники, архитекторы, дизайнеры и многие другие специалисты.

Частный случай центрального проецирования – параллельное проецирование, когда центр проецирования удален в бесконечность, при этом проецирующие лучи можно рассматривать как параллельные проецирующие прямые. Положение проецирующих прямых относительно плоскости проекций определяется направлением проецирования S (рис.4). В этом случае полученное изображение называют параллельной проекцией объекта.

При параллельном проецировании сохраняются свойства центрального и добавляются следующие:

проекции параллельных прямых параллельны между собой;

отношение отрезков прямой равно отношению их проекций;

отношение отрезков двух параллельных прямых равно отношению их проекций.

В свою очередь параллельные проекции подразделяются на прямоугольные, когда проецирующие лучи перпендикулярны плоскости проекций, и косоугольные, когда направление проецирования образует с плоскостью проекций угол не равный 90⁰.

Рисунок 4. Параллельное проецирование

Дата добавления: 2013-12-13