Взаимное расположение точек

Рассмотрим три основных варианта взаимного расположения точек, в зависимости от соотношения координат определяющих их положение в пространстве:

1. Рассмотрим точки А и В (рис.13), все три координаты которых отличаются, их взаимное расположение можно оценить по удаленности к плоскостям проекций:

- YА>YВ. Тогда точка А расположена дальше от плоскости П2 и ближе к наблюдателю, чем точка В;

- ZА>ZВ. Тогда точка А расположена дальше от плоскости П1 и ближе к наблюдателю, чем точка В;

- XА<XВ. Тогда точка В расположена дальше от плоскости П3 и ближе к наблюдателю, чем (при взгляде слева) точка А.

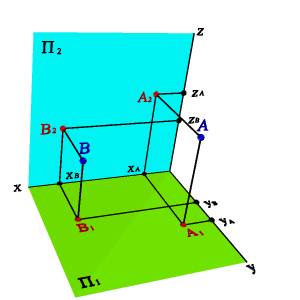
а) модель б)эпюр

Рисунок 13. Взаимное расположение точек

2. На рисунке 14 представлены точки А, В, С, D, у которых одна из координат совпадает, а две другие отличаются, их взаимное расположение можно оценить по удаленности к плоскостям проекций следующим образом:

– YА=YВ=YD, то точки А, В и D равноудалены от плоскости П2 и их горизонтальные и профильные проекции расположены, соответственно, на прямых А1В1//x12 и А3В3// z. Геометрическим местом таких точек служит плоскость, параллельная П2;

– ZА=ZВ=ZС, то точки А, В и С равноудалены от плоскости П1 и их фронтальные и профильные проекции расположены, соответственно, на прямых А2В2//x12 и А3С3// y. Геометрическим местом таких точек служит плоскость, параллельная П1;

– XА=XC=XD, то точки А, C и D равноудалены от плоскости П3 и их горизонтальные и фронтальные проекции расположены, соответственно, на прямых А1C1// y и А2D2//z. Геометрическим местом таких точек служит плоскость, параллельная П3.

3. Если у точек равны две одноименные координаты, то они называются конкурирующими. Конкурирующие точки расположены на одной проецирующей прямой. На рис. 14. даны три пары таких точек, у которых:

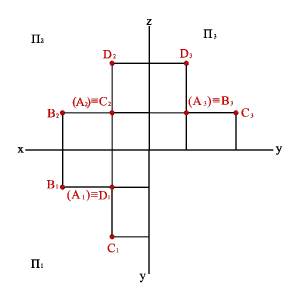
а) модель б) эпюр

Рисунок 14. Конкурирующие точки

XА=XD;YА=YD;ZD>ZА;

XA=XC;ZA=ZC;YC>YA;

YA=YB;ZA=ZB;XB>XA.

Соответствующие проекции конкурирующих точек совпадают.

Различают: горизонтально конкурирующие точки А и D, расположенные на горизонтально проецирующей прямой АD; фронтально конкурирующие точки A и C расположенные на фронтально проецирующей прямой AC; профильно конкурирующие точки A и B, расположенные на профильно проецирующей прямой AB.

При проецировании на соответствующую плоскость проекций одна точка «закроет» другую точку, конкурирующую с ней, соответствующая проекция которой окажется невидимой.

Тест на тему "Проекции точки"

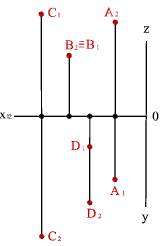
Точка С находится в первой четверти?

Да

Нет

Точка В находится во второй четверти?

Да

Нет

Точка А находится в первой четверти?

Да

Нет

Точка Д находится в третьей четверти?

Да

Нет

Точка Д лежит на горизонтальной плоскости проекций?

Да

Нет

Дата добавления: 2013-12-13