
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Архитектура СУД
|
|
|
|
Задание 9. Моделирование задачи линейного программирования
Задача 8. Поиск решения
Задача 7. Моделирование движения материальной точки, заданной параметрически
Задача 6. Моделирование прямолинейного движения материальной точки
Задача 4. Расчет стипендии учебной группы
Задача 3. Расчет периметра и площади прямоугольного треугольника
Задача 2. Случайное число
Задача 1. Моделирование физического процесса
Примеры решения задач
Скорость V тела, падающего в воздухе без начальной скорости, в момент времени t равна
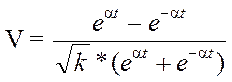 , a= , a= . .
|
Где k - коэффициент сопротивления среды, g - ускорение свободного падения.
Требуется составить электронную таблицу для расчета скорости тела в произвольный момент времени t³0 по заданным значениям k=0,001 и g=9,8.
Построим проект таблицы. В проекте определяем, в каких ячейках будут содержаться числа, текст, формулы.
| A | B | |
| Расчет скорости падения тела | ||
| Исходные данные: | ||
| Ускорение g свободного падения | 9,8 | |
| Коэффициент k сопротивления среды | 0,001 | |
| Момент времени t | ||
| Промежуточные формулы: | ||
| Корень из k | =КОРЕНЬ(B4) | |
| Показатель экспоненты | =B8*B3*B5 | |
| Возрастающая экспонента | =EXP(B9) | |
| Убывающая экспонента | =EXP(-B9) | |
| Скорость V | =(B10-B11)/(B8*(B10+B11)) |
Отформатируем таблицу и зададим момент времени t равным, например 10с (Рис. 86.).
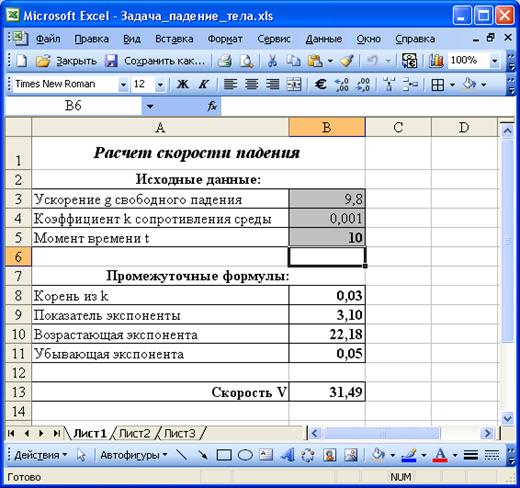
Рис. 86. Расчет скорости падения
Найти сумму минимального и максимального числа из 10 заданных в диапазоне от 2 до 7 случайных чисел.
Для вычисления случайного числа можно воспользоваться функцией СЛЧИС(). Но эта функция задает случайное число в диапазоне от 0 до 1 ([0,1)).
Чтобы найти случайное число на отрезке [ a, b ], надо спроектировать отрезок [0,1) на отрезок [ a, b ]. Для этого составим формулу:
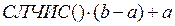 Ф(3)
Ф(3)
Теперь спроектируем таблицу (Рис. 87.):
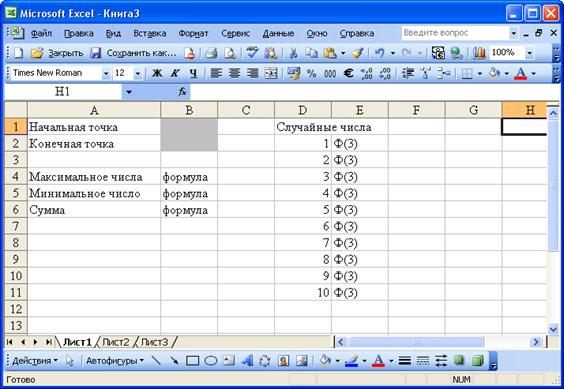
Рис. 87. Проект таблицы для задачи 2
Теперь занесем исходные данные и формулы, не забывая, что ссылки на начальную и конечную точки должны быть абсолютными.
| Ячейка | Содержимое |
| B1 | |
| B2 | |
| E1 | =СЛЧИС()*($B$2-$B$1)+$B$1 |
| E2 - E11 | копируем формулу из ячейки E1 |
| B4 | =МАКС(E2:E11) |
| B5 | =МИН(E2:E11) |
| B6 | =B5+B6 |
В результате может получиться таблица, представленная на Рис. 88. Результат может отличаться из-за функциональной работы функции СЛЧИС().
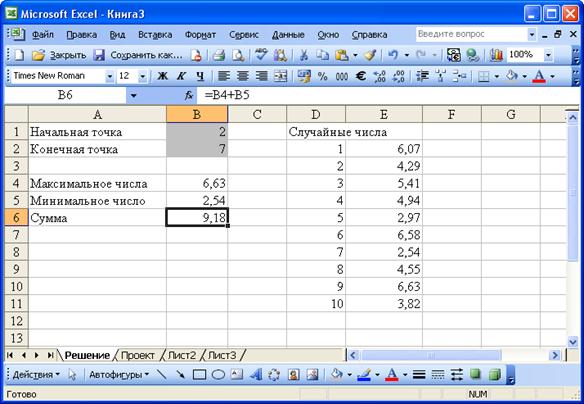
Рис. 88. Решение задачи 1
Построить таблицу значений периметра и площади прямоугольного треугольника при изменении длин его катетов от 1см до 10см с шагом 1см.
Периметр прямоугольного треугольника вычисляется по формуле:
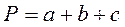
где a,b, - катеты, c –гипотенуза, которая вычисляется по формуле:
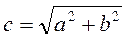
Площадь прямоугольного треугольника вычисляется по формуле:
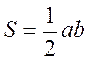
Для решения задачи построим шапку таблицу:
| А | В | С | D | E | |
| Катеты | Гипотенуза | Периметр | Площадь | ||
| a | b | c | |||
Теперь занесем формулы. В столбец А занесем значения катета a=1, в столбец
В – значения катета b от 1до 10 с шагом 1.
| А | В | С | D | E | |
| Катеты | Гипотенуза | Периметр | Площадь | ||
| a | b | c | |||
В ячейку С3 запишем формулу, вычисляющую гипотенузу: =КОРЕНЬ(А3^2+B3^2), в ячейку D3 запишем формулу: =A3+B3+C3, в ячейку E3 запишем формулу: =(1/2)*A3*B3
| А | В | С | D | E | |
| Катеты | Гипотенуза | Периметр | Площадь | ||
| a | b | c | |||
| =КОРЕНЬ(А3^2+B3^2) | =A3+B3+C3 | =(1/2)*A3*B3 | |||
| … | |||||
Теперь скопируем формулы третьей строки во все остальные строки
(Рис. 89.). Отформатируем формат представления чисел до 2 знаков после запятой.
Заметим, что во всех формулах используются относительные адреса ячеек.
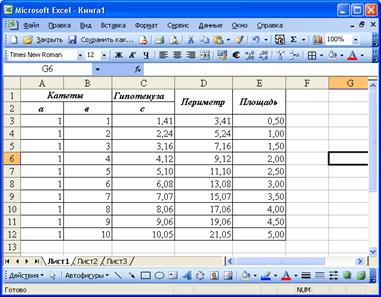
Рис. 89. Решение задачи 2
Теперь добавим строки, в которых катет a будет равен 2 (Рис. 90.), не забывая копировать в них формулы.
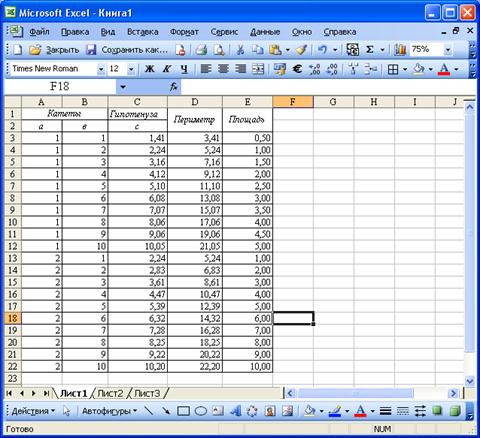
Рис. 90. Решение задачи 2 с добавление данных
Так же можно добавить строки с другими значениями катета a.
Необходимо составить расчетную ведомость на выдачу стипендии группе студентов, условно состоящей из 5 человек. Исходными данными являются:
1. Общий стипендиальный фонд, выделенный на группу (рубли);
2. Минимальная стипендия M (рубли),
3. Студенческий коэффициент K, на который умножается минимальная стипендия для вычисления значения стипендии каждого студента;
4. Успеваемость каждого студента, выраженная в виде его среднего рейтинга R за семестр;
5. Количество двоек Д каждого студента за сессию.
Стипендия конкретного студента складывается из стипендии, одинаковой для всех успевающих студентов с рейтингом не ниже 30 (общая), и дополнительной стипендии, размер которой зависит от успеваемости студента и общего стипендиального фонда (добавочная).
Для решения задачи используются следующие формулы:
| Стипендия = Общая стипендия + Добавочная стипендия | Ф(1) | ||||||||||||||||
| Общая стипендия = | 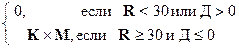
| Ф(2) | |||||||||||||||
| Добавочная стипендии = | Баллы, превышающие R=35 | ´ | Добавка за 1 балл | Ф(3) | |||||||||||||
| Баллы, превышающие R=35 | = | 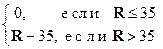
| Ф(4) | ||||||||||||||
| Найдем добавку за 1 балл: | |||||||||||||||||
| Общий фонд = Сумма общих стипендий | Ф(5) | ||||||||||||||||
| Добавочный фонд = Стипендиальный фонд - Общий фонд | Ф(6) | ||||||||||||||||
| Добавка за 1 балл | = | Добавочный фонд Сумма баллов, превышающих R=35 | Ф(7) | ||||||||||||||
Создание таблицы начинается с подготовки ее проекта (Рис. 91.).
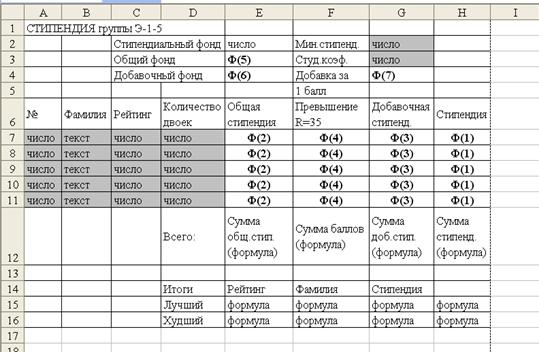
Рис. 91. Проект таблицы для задачи 3
Теперь будем заполнять таблицу. Сначала занесем текстовые значения, потом внесем исходные данные (серые ячейки в таблице), которые приведены на рисунке 92.
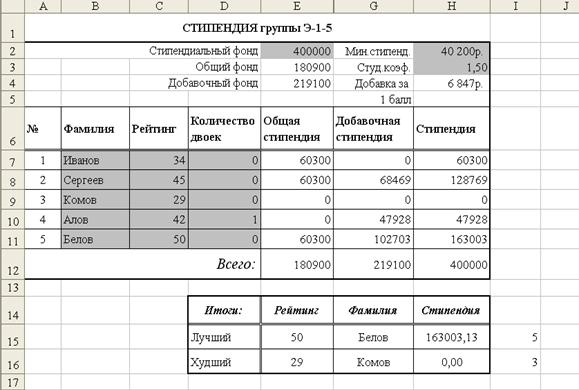
Рис. 92. Результирующая таблица задачи 3
Теперь запишем наши формулы, используя в них ссылки на соответствующие ячейки таблицы.
| Формула | Ячейка | Вид формулы в Excel |
| H7 | =E7+G7 | |
| E7 | =если(или(C7<30;D7>0);0;$G$3*$G$2) или =если(и(C7>=30;D7<=0);$G$3*$G$2;0) | |
| G7 | =F7*$G$4 | |
| F7 | =если(C7<=35;0;C7-35) или =если(C7>35;C7-35;0) | |
| E3 | =E12 | |
| E4 | =E2-E3 | |
| G4 | =E4/F12 |
После этого в ячейках E3 и G4 появится результат – сообщение об ошибке, т.к. в ячейках E12 и F12 пока нет данных. Чтобы получить данные в этих ячейках и записать необходимые формулы, надо сначала скопировать формулы из ячеек E7, F7, G7, H7 в соответствии с нашим проектом (на строки 8, 9, 10 и 11), а затем в ячейках E12, F12, G12, H12 записать формулы суммирования.
| Ячейка | Вид формулы в Excel |
| E12 | =E7+E8+E9+E10+E11 или =СУММ(E7:E11) |
| F12 | =F7+F8+F9+F10+F11 или =СУММ(F7:F11) |
| G12 | =G7+G8+G9+G10+G11 или =СУММ(G7:G11) |
| H12 | =H7+H8+H9+H10+H11 или =СУММ(H7:H11) |
Теперь заполним нижнюю часть таблицы с подведенными итогами:
| Ячейка | Вид формулы в Excel |
| E15 | =МАКС(C7:C11) |
| E16 | =МИН(C7:C11) |
| H15 | =ПОИСКПОЗ(E15;C7:C11;0) |
| F15 | =ИНДЕКС(B7:B11;H15) |
| G15 | =ИНДЕКС(H7:H11;H15) |
| H16 | =ПОИСКПОЗ(E16;C7:C11;0) |
| F16 | =ИНДЕКС(B7:B11;H16) |
| G16 | =ИНДЕКС(H7:H11;H16) |
В результате получим таблицу, представленную на Рис. 92.
Задача 5. Построение графика функции sin(x)
Построить график функции Sin(x) на отрезке [-3,3].
Так шаг разбиения отрезка [ a,b ] на n частей вычисляется по формуле:
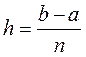
Где n – количество точек разбиения.
Каждая точка отрезка вычисляется по формулам:
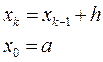
| 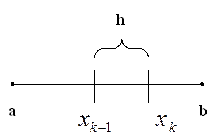
|
В нашем примере a =-3, b =3. Количество точек n примем равным 40.
Построим проект таблицы с указания начальной точки, конечной точки отрезка и шага. Для вычисления шага запишем формулу, в которой будут использованы ссылки на соответствующие ячейки, содержащие числа.
| A | B | C | D | E | |
| x | sin(x) | Начальная точка | -3 | ||
| Конечная точка | |||||
| Количество точек | |||||
| Шаг | =(E2-E1)/E3 | ||||
Теперь в ячейку A2 запишем ссылку на начальную точку, а в ячейку A3 запишем формулу вычисления следующей точки отрезка, в ячейку B2 запишем формулу, вычисления sin(x):
| A | B | C | D | E | |
| x | sin(x) | Начальная точка | -3 | ||
| =E1 | =sin(A2) | Конечная точка | |||
| =A2+$E$4 | Количество точек | ||||
| Шаг | =(E2-E1)/E3 | ||||
Теперь скопируем формулы из ячейки A3 в ячейки столбца А так, чтобы получить 40 точек исходного отрезка, и формулу из ячейки B2 скопируем до 42 строки.
| A | B | C | D | E | |
| x | sin(x) | Начальная точка | -3 | ||
| -3 | -0,141 | Конечная точка | |||
| -2,85 | -0,287 | Количество точек | |||
| -2,7 | 0,427 | Шаг | =(E2-E1)/E3 | ||
| … | |||||
| 0,141 |
Для построения графика воспользуемся Мастером диаграмм. Для этого можно выделить данные столбцов A и B, и нажать на панели инструментов кнопку вызова Мастера диаграмм. Выберем Точечную диаграмму, установим легенды диаграммы, проведем форматирование области построения.
В итоге получаем график функции sin(x) (Рис. 93.).
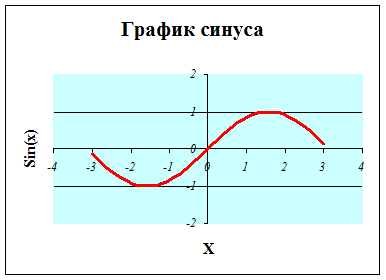
Рис. 93. График функции sin(x)
Если теперь изменять начальную или конечную точки отрезка [ a, b ], то Excel автоматически проведет перерасчет формул и построит соответствующий им график (Рис. 94.)
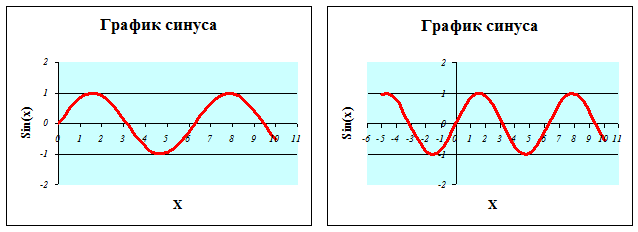
Рис. 94. График функции sin(x) на разных интервалах
Ускорение a, скорость V и координата X материальной точки массы m, совершающей прямолинейное движение под действием силы, равной Fcos(wt), определяются соотношениями
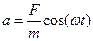 ; ;
| (2) |
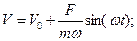
| (3) |
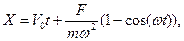
| (4) |
где F и w - постоянные величины; Vо - скорость точки в начальный момент. Предполагается, что в начальный момент времени координата X равна нулю.
а) Построить таблицу, содержащую значения ускорения а, скорости V и координаты X в пятидесяти равноотстоящих моментах.
б) Построить графики изменения величин a, V и X во времени.
в) Найти минимальное и максимальное значения а, V и X, а также соответствующие им моменты времени t.
г) Построить зависимость координаты точки от скорости X(V).
а) Для решения задачи построим проект таблицы (Рис. 95.).
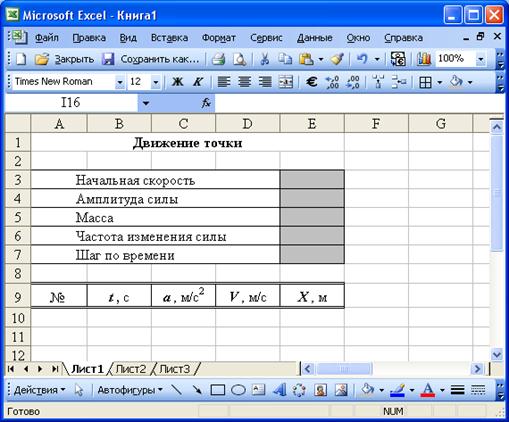
Рис. 95. Проект таблицы задачи 6
Зададим начальные значения V0 =0,15м/с, F =1, ω =2, m =1, шаг по времени = 0,06 (Рис. 96.).
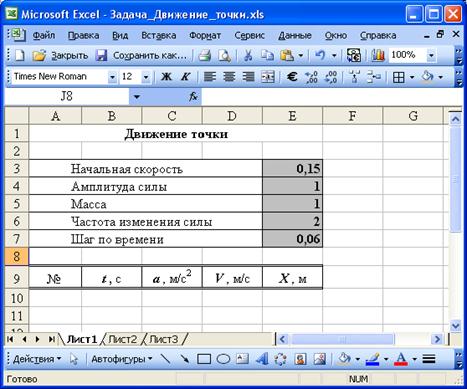
Рис. 96. Исходные данные
Занесем в ячейки таблицы формулы:
| Ячейка | Вид формулы в Excel |
| B10 | =0 |
| B11 | =B10+$E$7 |
| C10 | =$E$4/$E$5*cos($E$6*B10) |
| D10 | =$E$3+$E$4/($E$5*$E$6)*sin($E$6*B10) |
| E10 | =$E$3*B10+$E$4/($E$5*$E$6^2)*(1-cos($E$6*B10)) |
| A10 – A60 | 1,2 – далее автозаполнение до числа 51, задано 50 точек разбиения. |
Далее копируем формулы из ячеек B11, C10, D10, E10 до 61 строки (Рис. 97.)
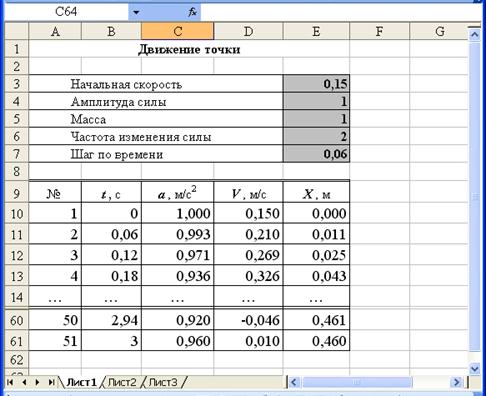
Рис. 97. Заполнили таблицу формулами
б) Теперь построим графики изменения величин a, V и X во времени. Для этого выделим столбец B (время) для задания точек по оси абсцисс. Выделим столбцы С, D, E для задания точек по оси ординат. Затем с помощью Мастера диаграмм выберем точечную диаграмму, зададим легенды, проведем форматирование области построения. В результате можно получить график, представленный на Рис. 98.
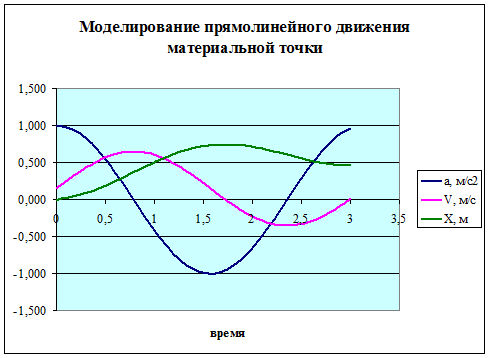
Рис. 98. График движения материальной точки
в) Найдем минимальное и максимальное значения а, V и X, а также соответствующие им моменты времени t.
Для этого спроектируем таблицы (Рис. 99.).
Рис. 99. Проекты таблицы для поиска максимального и минимального значений
А потом занесем соответствующие формулы:
| Ячейка | Вид формулы в Excel |
| J3 | =МИН(C10:C60) |
| K3 | =МИН(D10:D60) |
| L3 | =МИН(E10:E60) |
| J4 | =ИНДЕКС($B$10:$B$60;ПОИСКПОЗ(J3;C10:C60;0)) |
| K4 | =ИНДЕКС($B$10:$B$60;ПОИСКПОЗ(K3;D10:D60;0)) |
| L4 | =ИНДЕКС($B$10:$B$60;ПОИСКПОЗ(L3;E10:E60;0)) |
| J9 | =МАКС(C10:C60) |
| K9 | =МАКС(D10:D60) |
| L9 | =МАКС(E10:E60) |
| J10 | =ИНДЕКС($B$10:$B$60;ПОИСКПОЗ(J9;C10:C60;0)) |
| K10 | =ИНДЕКС($B$10:$B$60;ПОИСКПОЗ(K9;D10:D60;0)) |
| L10 | =ИНДЕКС($B$10:$B$60;ПОИСКПОЗ(L9;E10:E60;0)) |
В результате получим таблицы (Рис. 100.)
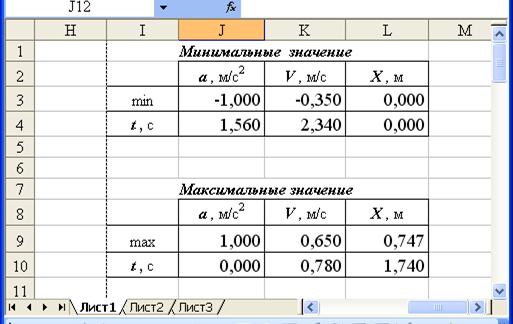
Рис. 100. Результирующие таблицы
г) Построим теперь зависимость координаты точки от скорости X(V). Для этого по оси абсцисс отложим данные столбца D (скорость точки), а по оси ординат – данные столбца E (координата точки). Построим точечную диаграмму (Рис. 101.).
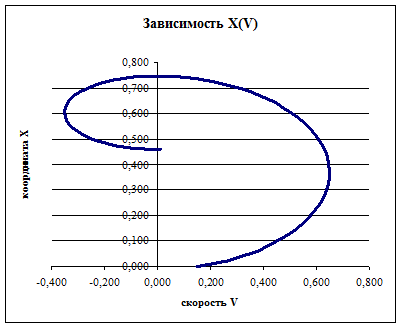
Рис. 101. График зависимости X(V)
Движение материальной точки на отрезке времени [a,b] задается параметрически:
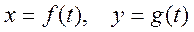
Требуется построить графики функций:
- на первом листе: Y(x) – траекторию движения точки;
- на втором листе: Vx(t), Vy(t), V(t) – графики скоростей точки;
- на третьем листе: S(t) – путь точки.
Для решения задачи зададим функции движения материальной точки.
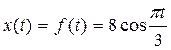
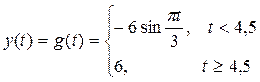
Интервал времени – [0,6], количество точек разбиения интервала n = 40.
Формулы решения задачи:
Точки временного интервала: 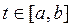 ,
, 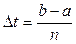 ,
, 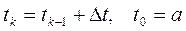
Расчет скорости: 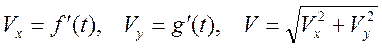
В нашем случае:
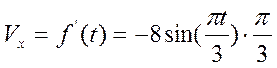
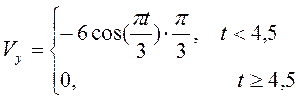
Расчет пути: 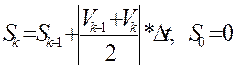
Построим проект таблицы (Рис. 102.):
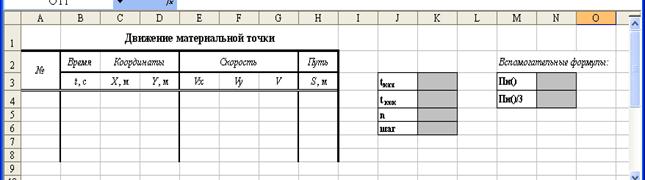
Рис. 102. Проект таблицы
Теперь занесем исходные данные:
| Ячейка | Вид формулы в Excel |
| K3 | |
| K4 | |
| K5 | |
| K6 | =(K4-K3)/K5 |
| N3 | =ПИ() |
| N4 | =ПИ()/3 |
| A4 – A44 | номера точек |
Теперь будем заносить формулы для вычислений:
| Ячейка | Вид формулы в Excel |
| Формулы для расчета точек временного интервала | |
| B4 | =K3 |
| B5 | =B4+$K$6 |
| Формулы для расчета координат | |
| C4 | =8*COS($N$4*B4) |
| D4 | =ЕСЛИ(B4<4,5;-6*SIN($N$4*B4);6) |
| Формулы для расчета компонент скорости | |
| E4 | =8*SIN($N$4*B4)*$N$4 |
| F4 | =ЕСЛИ(B4<4,5;-6*COS($N$4*B4)*$N$4;0) |
| G4 | =КОРЕНЬ(E4^2+F4^2) |
| Формулы для расчета пути | |
| H4 | =0 |
| H5 | =H4+ABS((G4+G5)/2)*$K$6 |
Скопируем теперь формулы на все строки таблицы (Рис. 103.).
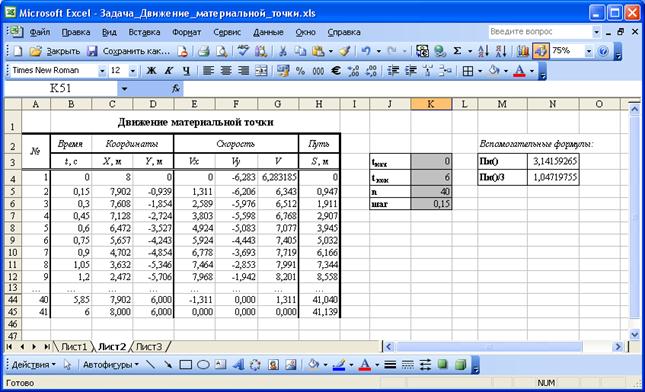
Рис. 103. Заполненная таблица
Теперь будем строить необходимые графики.
На первом листе построим траекторию движения точки Y(x). Для этого выделим данные столбцов C (координата x) и D (координата y) и построим точечную диаграмму, указав Мастеру диаграмм, что строить диаграмму надо на отдельном листе (Рис. 104.). В результате на рабочей книге появиться отдельный лист с диаграммой (Рис. 105.)
Рис. 104. Выбор отдельного листа для диаграммы
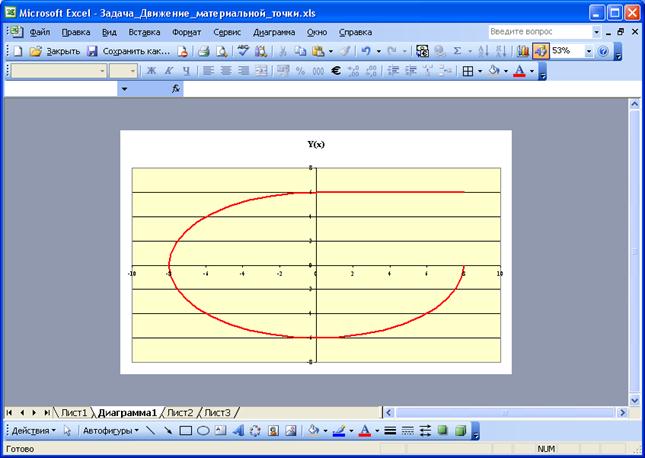
Рис. 105. График У(x)
На втором листе построим графики скоростей Vx(t), Vy(t), V(t), которые зависят от времени. Значит, выделяем данные столбца B, а затем при нажатой клавише Ctrl выделяем данные столбцов E, F, G. Строим точечную диаграмму (Рис. 106.).
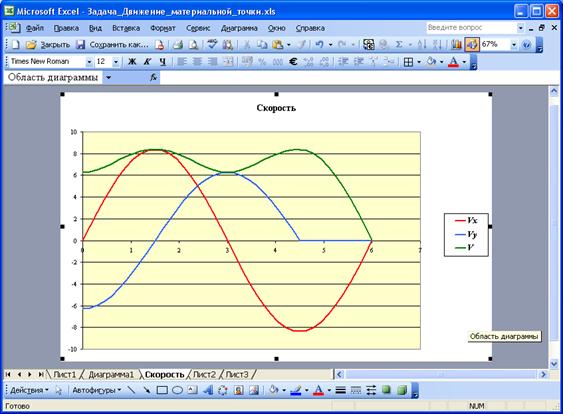
Рис. 106. График скоростей
На третьем листе построим график пути точки S(t), выделив данные столбцов B и H (Рис. 107.).
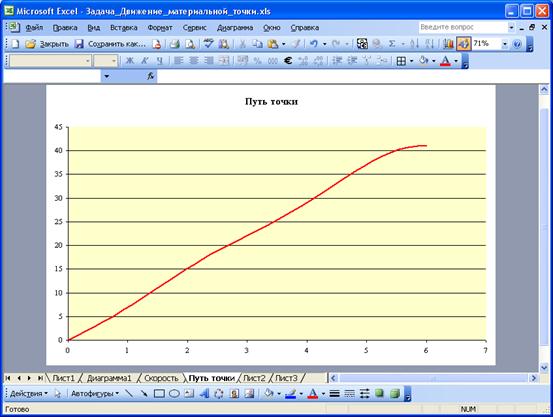
Рис. 107. График пути точки
"На фирме могут работать директор, главный бухгалтер, ведущие инженеры и специалисты.
Известно, что директора и главного бухгалтера может быть только по 1 человеку, ведущих инженеров может быть не более 5, но один – обязательно, специалистов – не более 10 и не менее 2 человек.
Зарплата каждого сотрудника зависит от разряда. Таблица разрядов и окладов задана. Известно, что директор тарифицируется по 9 разряду, главный бухгалтер – по 8 разряду, ведущий инженер – по 7 разряду, специалист – по 5 разряду.
Требуется определить количество сотрудников фирмы так, чтобы суммарная заработная плата не превысила 13000 рублей."
Для решения создадим таблицу с начальными данными (Рис. 108.):
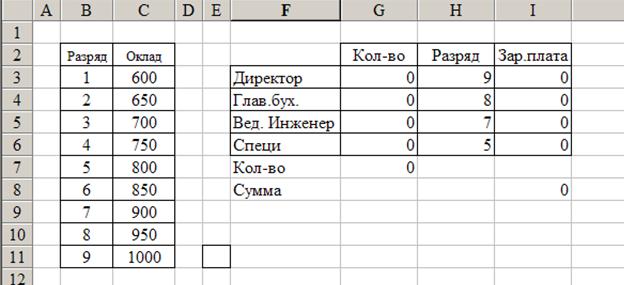 |
Рис. 108. Проект таблицы с начальными данными
Количество ставок по должностям в начале принимает значение 0.
Зарплата каждого сотрудника зависит от разряда и количества ставок. Поэтому в ячейку I3 занесем формулу:
=ПРОСМОТР(H3;$B$3:$B$11;$C$3:$C$11)*G3
В остальные ячейки столбца "Зар.плата" скопируем эту формулу.
В ячейку G7 занесем формулу суммирования:
=СУММ(G3:G6)
В ячейку I8 занесем формулу:
=СУММ(I3:I6)
Теперь, используя специальную возможность Excel " Поиск решения ", найдем решение задачи.
Зададим целевую ячейку I8 – общая сумма зарплат. Можно задать ее значение как максимальное, как минимальное или равное определенному значению. В нашей задаче общая сумма зарплат не должна превышать 13000, поэтому выберем переключатель " максимальное значение " и зададим условие отбора $I$8<=13000
Изменять надо ячейки, содержащие количество ставок, - G3:G6.
Зададим ограничения, используя кнопку " Добавить " (Рис. 109.).
Все значения ячеек G3:G6 – должны быть целочисленными:
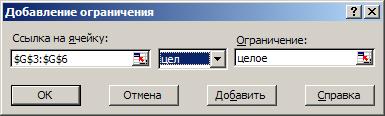
Рис. 109. Окно запроса для добавления ограничений
В ячейках G3 и G4 должно быть число 1.
Значение в ячейке G5 должно быть больше и равным 1 и меньшим или равным 5. Значение в ячейке G6 должно быть больше и равным 2 и меньшим или равным 10. На рис. 110 приведено окно запроса " Поиск решения " с установленными параметрами задачи.

Рис. 110. Параметры задачи
Чтобы получить результат, достаточно нажать кнопку " Выполнить":. После чего Excel, используя алгоритм перебора, подбирает значения в изменяемых ячейках так, чтобы в целевой ячейке было максимальное значение. Если решение будет найдено (Рис. 111.), то надо сохранить найденное решение и Excel выдаст результат поиска (Рис. 112.)
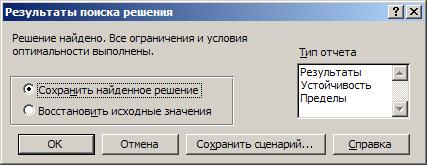
Рис. 111. Решение найдено
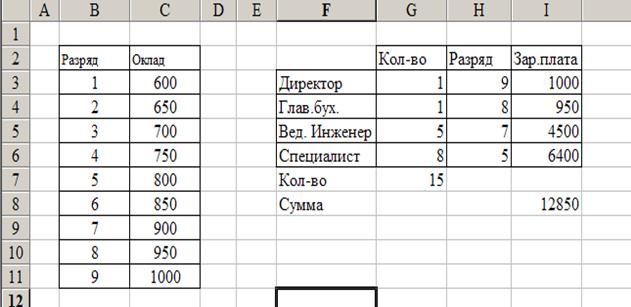
Рис. 112. Результат решения задачи
В ходе производственного процесса из листов материала получают заготовки деталей двух типов А и Б тремя различными способами, при этом количество получаемых заготовок при каждом методе различается (данные в таблице):
| Тип заготовки | Количество заготовок | ||
| Способ 1 раскроя | Способ 2 раскроя | Способ 3 раскроя | |
| А | 6 | 4 | 10 |
| Б | 2 | 5 | 3 |
Необходимо выбрать оптимальное сочетание способов раскроя, для того чтобы получить 600 заготовок первого типа и 400 заготовок второго типа при расходовании наименьшего количества листов материала.
Чтобы решить задачу, построим математическую модель.
Математическая модель
Параметрами, значения которых требуется определить, являются количества листов материала, которые будут раскроены различными способами:
X1 – количество листов, раскроенное способом 1;
X2 – количество листов, раскроенное способом 2;
X3 – количество листов, раскроенное способом 3;
Тогда целевая функция, значением которой является количество листов материала, примет вид:
F=X1 + X2 + X3
Ограничения определяются значениями требуемых количеств заготовок типа А и Б, тогда с учетом количеств заготовок, получаемых различными способами, должны выполняться два равенства:
6X1 + 4X2 + 10X3 = 600
2X1 + 5X2 + 3X3 = 400
Кроме того, количества листов не могут быть отрицательными!
Таким образом, необходимо найти удовлетворяющие ограничениям значения параметров, при которых целевая функция принимает минимальное значение.
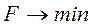
Получили задачу линейного программирования.
Построим проект таблицы (Рис. 113.).
Рис. 113. Проект таблицы
Зададим начальные значения. Так в ячейки B2, C2, D2 занесем число 0, т.к. количество листов не может быть отрицательным, но может отсутствовать в заготовке. В ячейки B3, B4 занесем ограничения на количество заготовок типа А (400) и типа В (200), заданные по условию задачи (Рис. 114.).

Рис. 114. Задание начальных значений
Теперь запишем формулы для расчета.
| Ячейка | Вид формулы в Excel | Примечание |
| B5 | =6*B2+4*C2+10*D2 | ограничение на заготовки типа А |
| B6 | =2*B2+5*C2+3*D2 | ограничение на заготовки типа В |
| E2 | =B2+C2+D2 | целевая функция |
После этого зададим условия решения задачи с помощью инструмента Поиск решении (Рис. 115.):
- Устанавливаем целевую ячейку E2, определяем ее значение как минимальное.
- Изменяться должны ячейки B2, C2, D2.
- Ограничения:
~ изменяемые ячейки должны быть целыми и положительными,
~ значение ячейки B5 должно быть равным количеству заготовок типа А, т.е. равным значению ячейки B3,
~ значение ячейки B6 должно быть равным количеству заготовок типа В, т.е. равным значению ячейки B4.
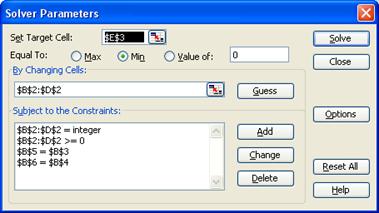
Рис. 115. Задание условий для поиска решения
Дав команду " Выполнить ", сохранив решение и построив диаграмму, получаем решение задачи (Рис.116.):
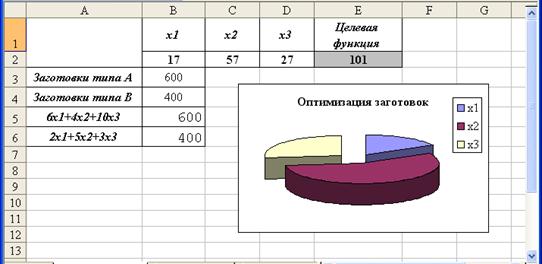
Рис. 116. Решение задачи
Отображает документы и связи между ними в виде карты документов организации, содержит концептуальный уровень и предметный воплощения.
Содержит:
- концептуальный
- логический
- предметное воплощение
| Почему? Кто? | Концептуальный уровень |
| Что? Когда? | Логический уровень |
| Как? Где? | Уровень предметного воплощения |
На концептуальном уровне определяется состояние документооброта, то есть, какие документы и БД должны входить в СУД и взаимно связи, объем СУД, количество пользователей и основания потоки документооборота.
На логическом уровне решается вопросы функциональных характеристик СУД (ввод и вывод данных, их обработка, безопасность, правила ведения, деловые интерфейсы и формы отчетов). Логический уровень определяет, что будет делать система и когда запускается каждый процесс. Логический уровень не привязан к компьютеру и может быть выполнен аппаратным и программным обеспечением. Необходим для определения процесса и разделения.
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 650; Нарушение авторских прав?; Мы поможем в написании вашей работы!