
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дифференциальные уравнения собственных линейных колебаний
|
|
|
|
Собственные линейные колебания системы.
Колебания системы с одной степенью свободы
Движение системы с одной степенью свободы описывается одним уравнением Лагранжа второго рода.
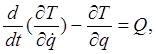 (1)
(1)
где 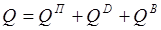 .
.
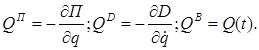
Часть обобщенной силы Q(t) получается от возмущающих сил, зависящих прежде всего от t.
Если в (1): Q =QП – собственные свободные колебания,
Q =QП + QD – затухающие колебания,
Q =QП + QВ – вынужденные колебания.
Рассмотрим движение системы матерериальных точек с голономными, удерживающими, идеальными, стационарными связями.
Ее кинетическая энергия 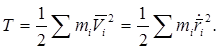 (1)
(1)
При допущении о стационарных связях 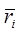 зависит от t только через обобщенную координату q, следовательно:
зависит от t только через обобщенную координату q, следовательно:
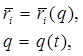
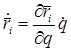 , (2)
, (2)
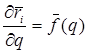 .
.
(2) ® (1): 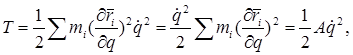 (3)
(3)
где 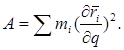
Величина А, как и 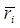 , может завесить от
, может завесить от 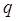 и не зависит от
и не зависит от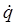
A = A(q).
Полагая q малой величиной и разложив A(q) в окрестности q = 0 (вблизи устойчивого равновесия) в степенной ряд, имеем:
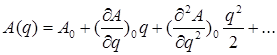 .
.
«0» означает, что соответствующую величину надо определять при q = 0.
Сохранив лишь члены выше второго порядка (т.е. оставляя первый член) (3) примет вид:
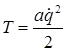 , (а)
, (а)
где α = A(q) = 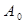 ;
;
α – коэффициент инерции (если 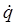 скорость - размерность массы;
скорость - размерность массы; 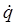 угловая скорость – размерность момента инерции).
угловая скорость – размерность момента инерции).
Для потенциальной энергии
П = П(q) – только функция q.
Разложив П в ряд в окрестности q = 0, получим
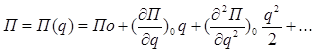 .
.
По = Пmin (по теореме Лагранжа – Дирихле). Примем По = 0
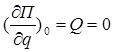 - положение равновесия,
- положение равновесия,
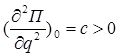 - устойчивое равновесие.
- устойчивое равновесие.
Отбрасывая слагаемые третьего и более высоких порядков малости, имеем:
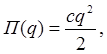 (б)
(б)
где с – квазиупругий коэффициент (коэффициент жесткости).
Уравнение Лагранжа для консервативных сил
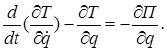
(а) ® 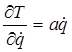 ,
,
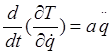
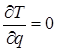 , т.к. Т не зависит от q.
, т.к. Т не зависит от q.
(б) ® 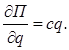
Т.о. уравнение Лагранжа второго порядка примет вид
|

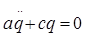 (1)- уравнение собственных колебаний системы с одной
(1)- уравнение собственных колебаний системы с одной
Т.о. нами получено линейное д.у.д. →
Замена точного диф. уравнения движения (отбрасывая члены более высоких порядков) линейным называется линеаризацией.
Поделим обе части полученного д.у.(1) на а и обозначим 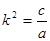 , получим
, получим

|
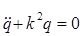 - линейное однородное д.у. второго порядка с постоянным
- линейное однородное д.у. второго порядка с постоянным
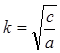 - круговая (циклическая) частота колебаний.
- круговая (циклическая) частота колебаний.
Характеристическое уравнение 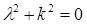 ; корни мнимые l1,2 = ± ki.
; корни мнимые l1,2 = ± ki.
На основе теории диф. уравнений его решение

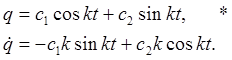
с1, с2 – произвольные постоянные.
Начальные условия при t = 0

|
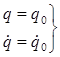
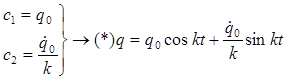 - одна из 2х основных форм
- одна из 2х основных форм
Выражение для q в амплитудной форме

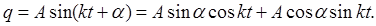
Собственные линейные колебания являются гармоническими.
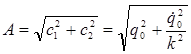 - амплитуда колебаний.
- амплитуда колебаний.
Т.о. А – const и определяется начальными условиями.
a - начальная фаза колебаний (0 - 2p),
kt + a - фаза колебаний ( при t = 0),
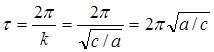 - период.
- период.
t - const; не зависит от А и, следовательно, начальных условий.
Независимость t от А называется изохронностью колебаний.
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 1294; Нарушение авторских прав?; Мы поможем в написании вашей работы!