
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 10. Валеологическое воспитание населения
|
|
|
|
Конституцию РФ нужно воспринимать как Священное Писание, как гражданскую Библию, рассуждал вчера в Госдуме в рамках лекций, посвященных 20-летию Основного закона страны госсекретарь России в 1991-1992 годах Геннадий Бурбулис, участвовавший вместе с Борисом Ельциным в подписании Беловежского соглашения. Обществу не хватает конституционного консенсуса, считает он, его нужно к нему принуждать. Заодно он поделился мнением о недостатках демократии и предложил свой "идеал" модели управления.
ШШшя
Задачи
1.
Классификация систем
Вопрос № 3. Виды политической системы общества
Вопрос № 1. Понятие и элементы политической системы общества
Вопрос № 4. Место государства в политической системе
Вопрос № 3. Виды политической системы общества
Под гидрогеологическими районами понимают территории, характеризующиеся общностью гидрогеологических условий. Выделение таких районов и составляет сущность гидрогеологического районирования, которое проводится в разном масштабе, с учетом разных факторов и целей.
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Природа слова и перевод (Крупнов)
Библиография Правовые акты
Вопросы и задания для самоконтроля.
Е
(?
Пятый вопрос. Взаимодействие налоговых органов с судом.
Четвертый вопрос. Актуальные аспекты взаимодействия налоговых органов и МВД России.
Третий вопрос. Современные аспекты взаимодействия налоговых органов и Федеральной таможенной службой.
Второй вопрос. Современные аспекты взаимодействия налоговых органов и органов местного самоуправления.
|
|
|
Литература.
ГЛАВА 2. СЛУЧАИ, ДОПУСКАЮЩИЕ ПРИМЕНЕНИЕ ЭФФЕКТИВНЫХ ПРОЦЕДУР
ГЛАВА 1. ПОСТАНОВКА ЗАДАЧ ПРОЕКТИРОВАНИЯ ОПТИМАЛЬНЫХ ПРОГРАММНЫХ КОМПЛЕКСОВ
ВВЕДЕНИЕ
Оглавление
СЕВЕРО-КАВКАЗСКИЙ ГОРНО-МЕТАЛЛУРГИЧЕСКИЙ ИНСТИТУТ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
Принципы построения бюджетной системы Российской Федерации
Бюджетная система Российской Федерации
Машиностроение - общероссийской значение имеют такие его отрасли как энергетическое (турбины, генераторы), судостроение, станкостроение, приборостроение, электроника и электротехника. Особенностью машиностроительного комплекса является исключительно высокая концентрация производства в крупнейшем промышленном районе страны – Санкт-Петербургском.
Машиностроение - общероссийской значение имеют такие его отрасли как энергетическое (турбины, генераторы), судостроение, станкостроение, приборостроение, электроника и электротехника. Особенностью машиностроительного комплекса является исключительно высокая концентрация производства в крупнейшем промышленном районе страны – Санкт-Петербургском.
Б) М.В. Остроградский
А) Н.И. Лобачевский
В обстановке социального подъёма конца XVIII - начала XIX вв. интерес к науке стал расти и для математики наступило время плодотворного контакта с передовыми идеями французской школы Эпохи революции. Гурьев и Рахманов явились первыми выдающимися проводниками этих новых идей.
Вопрос 2. Снижение транзакционных издержек через появление денег. Сущность и функции денег. Ликвидность. Декретные деньги. Измерение предложения денег
Вопрос 2. Снижение транзакционных издержек через появление денег. Сущность и функции денег. Ликвидность. Декретные деньги. Измерение предложения денег
|
|
|
Триплетность. Каждой аминокислоте в генетическом коде соответствует определенная последовательность нуклеотидов (триплет или кодон). Различных нуклеотидов в ДНК 4(аденин, гуанин, цитозин, тимин), следовательно число сочетаний из 4 нуклеотидов по 3 составит 64 комбинации или триплета. 20 аминокислот кодируются 61 триплетом. 3 триплета являются стоп-кодонами, обрывающие трансляцию и прекращающие синтез белка. 1. УАА 2. УГА 3. УАГ.
Лекция 2. Технологическая схема создания и обновления ЦК
Классификация потребностей
По А.Маслоу:
Ресурсы Доход
1. Природные -> Рента
2. Трудовые -> Зарплата
3. Инвестиции -> Проценты
4. Бизнес -> Прибыль
Экономика отвечает на три главных вопроса:
· Что произволить? - альтернативные издержки
· Где производить? -
· Для кого производить? -
Уровниэкономики
1. Мегаэкономика
2. Макроэкономика
3. Мезоэкономика
4. Микроэкономика
5. Наноэкономика
Калькуляциястоимостидиплома
1. Плата -> 200тыс /год = 800тыс
2. Транспорт -> 600x10х4= 24 тыс
3. Жилье -> 40тыс х12х4= 1920тыс
4. Канцтовары -> 40тыс
5. Прочее ->
6. Пища -> 20тыс х 12х4 960тыс
7. Упущенная зарплата -> 15тыс x12x4=720тыс
Итого:
ОБЩАЯ ТЕХНОЛОГИЧЕСКАЯ СХЕМА
Общая технологическая схема создания и обновления цифровых карт и планов на основе данных дистанционного зондирования Земли (ДЗЗ) состоит из следующих этапов:
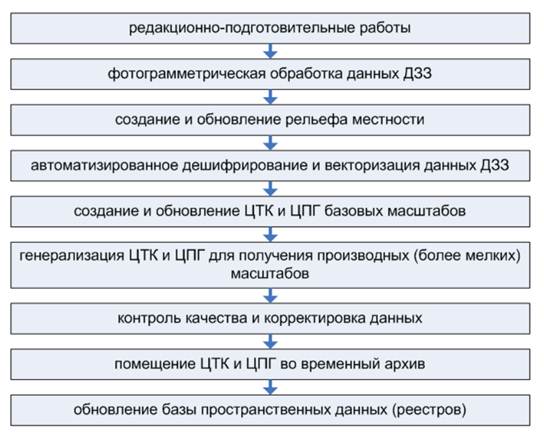
Рисунок 1. Общая схема создания и обновления ЦТК и ЦПГ
Целью редакционно-подготовительных работ является оценка полноты и качества исходных материалов, уточнение технологии и технологических особенностей выполнения работ в зависимости от требований заказчика, наличия основных и дополнительных исходных материалов.
К редакционно-подготовительным работам относятся:
- сбор исходных данных;
- входной контроль исходных данных;
- изучение района картографирования и исходных данных;
- отработка редакционно-технических указаний.
Фотограмметрическая обработка данных ДЗЗ включает в себя:
- создание проекта (создание и выбор активного профиля создание проекта формирование блока изображений проекта);
|
|
|
- измерение сети;
- уравнивание сети;
- построение цифровой модели рельефа и ортофотопланов (стереовекторизация, построение ЦМР в виде нерегулярной сети треугольников TIN, построение ЦМР в виде матрицы высот, создание ортофотоплана).
Результатом фотограмметрической обработки данных дистанционного зондирования является:
- создание цифровой модели рельефа и цифрового ортофотоплана;
- частичное или полное дешифрирование и стереовекторизация элементов содержания цифровой карты в стереорежиме (в модулях PHOTOMOD StereoDraw, PHOTOMOD StereoVectOr);
- определение метрических характеристик объектов местности, например, относительной высоты сооружений, форм рельефа (ям, обрывов и т.д.) и растительности (высоты деревьев). А также определение ширины дорог, рек, ручьев и т.д.
Создание и обновление рельефа местности выполняется для получения векторной формы представления рельефа местности (горизонтали, отметки высот и т.п.) для подготовки карт к изданию.
Автоматизированное дешифрирование и векторизация данных ДЗЗ предназначены для распознавания на снимках местности объектов и формирования их контуров в векторном виде для дальнейшего создания и обновления ЦТК и ЦПГ. Данная задача дополняет возможности дешифрирования и стереовекторизации комплекса PHOTOMOD.
Целью этапа создания и обновления ЦТК и ЦПГ является ввод и корректировка координат объектов местности, ввод и корректировка семантических характеристик, согласование топологических отношений объектов (примыканий, пересечений, общих границ). Цифровое описание объектов ЦТК и ЦПГ по точности, полноте, правилам описания контуров объектов обычно соответствует правилам подготовки (составления) карт некоторого базового масштаба. Для населенных территорий рекомендуемым масштабом является масштаб 1: 25 000.
Генерализация ЦТК и ЦПГ для получения производных масштабов выполняется для подготовки карт более мелких масштабов (например, подготовка карты масштаба 1: 50 000 по картам масштаба 1: 25 000 и так далее) для издания или специального применения (например, подготовка навигационных карт для авиации).
|
|
|
На этапе контроля качества и корректировки данных проводятся автоматические процедуры проверки качества и корректировки цифровых карт в формате SXF по выбранной схеме контроля.
Цель этапа помещения созданных и обновленных ЦТК и ЦПГ во временный архив заключается в накоплении готовых цифровых карт и планов для их применения в процедурах сводки смежных листов и формирования единых покрытий для обновления базы пространственных данных.
Обновление базы пространственных данных выполняется с помощью протоколов OGC WFS для передачи наборов данных в форматах SXF и GML, а также для обновления отдельных объектов и метаданных в реестрах [9, 10,11].
2. Вырожденность генетического кода. Одну аминокислоту могут кодировать несколько триплетов от 2 до 6 триплетов.
3. Однозначность или специфичность. Один триплет кодирует только одну аминокислоту.
4. Неперекрываемость. Один нуклеотид входит в состав только одного кодона.
5. Непрерывность. Кодоны не отделены один от другого, располагаются в цепи нуклеиновой кислоты линейно.
6. Универсальность. Генетический код одинаков у всех организмов на земле.
Направление реализации наследственной информации в клетки:
ДНК и-РНК белок.
Снижение транзакционных издержек специализации происходит с появлением денег, решающих проблему двойного согласования желаний покупателя и продавца путем продажи в обмен на конкретный товар абстрактного товара-посредника –денег, который затем можно легко поменять на любой товар.
2.1. Сущность и функции денег
Деньги – это нечто, принимаемое как посредник обмена товара на товар: Т-Д-Т’
Определение денег вытекает из выполняемых ими функций. То, что выполняет функции денег, а именно: средства платежа (посредничества обмена), средство сохранения ценности, единицы учета благ, и называется деньгами.
а) Средство платежа или посредник обмена. Бартер – это прямой обмен товаров на товары без посредства денег. Требуются значительные усилия, чтобы найти покупателя вашего товара, который одновременно предложит нужный вам товар. Деньги как посредник легко разрешают проблему двойного согласования желаний покупателя и продавца. Деньги имеют ряд преимуществ перед другими средствами обмена: они легко делимы на части без потери ценности и портативны.
б) Средство сохранения ценности между сделками. Недостаток в том, что деньги, не имеющие внутренней ценности, обесцениваются при росте цен товаров. На ту же сумму денег можно меньше купить. От таких денег стараются избавиться. Поскольку так поступают все, то бегство от денег протекает бурно и ведет к быстрой потере ликвидности. Ликвидность – это свойство денег легко обмениваться. Все другие товары имеют ограниченную ликвидность – их сложнее продать. Деньги как товар обладают наибольшей среди них способностью к сбыту – ликвидностью. Именно вследствие меньшей ликвидности ценные бумаги называют денежными суррогатами. Например, вексель – обязательство оплатить долг. Деньги, которые выполняют функцию сохранения ценности (покупательную силу, покупательную способность) между сделками, одновременно ликвидны. Если есть опасность их обесценивания между сделками, то от таких денег все постараются избавиться, заменить твердой валютой, и никто не захочет их брать. Несохранение ценности ведет к неликвидности денег.
в) Единица учета. Для выражения цен товаров в стандартных единицах. Приспосабливание денег к инфляции называется индексацией. При высокой инфляции цены контрактов выражают в относительно стабильной иностранной валюте.
2.2. Декретные деньги
Два типа денег: 1) Имеющие внутреннюю ценность в каком-либо другом использовании. 2) Декретные деньги.
Скот и медь как деньги. В древнейшее время в Риме скот играл роль денег; об этом свидетельствует самое название последних pecunia (от pecus - скот); кроме того, по свидетельству источников, еще в начале периода республики имущественные штрафы назначались в виде известного количества скота. Позже они начинают употреблять металл и именно медь, aes, откуда позднейшие выражения – aestimatio ["оценка"] и т.д. Первой чеканной монетой был as libralis – acc, равный 1 фунту меди.
Декретные (договорные) деньги. Они не имеют внутренней ценности. Стоимость их изготовления может быть в тысячи раз меньше, того, что на них написано и принимается рынком. Из-за опасности потери ликвидности и снижения покупательной силы в процессе инфляции декретные деньги не могут служить надежным средством накопления.
Декретные деньги принимаются населением как средство платежа потому, что правительство придает деньгам легальный статус, требуя оплаты ими налогов.
2.3. Измерение предложения денег
Широкий круг активов может выполнять функции денег. Поэтому трудно подвести черту и сказать: «Выше нее деньги, ниже нечто другое».
Измерение количества денег осуществляется в статистике с помощью денежных агрегатов.
Денежные агрегаты:
М0 – наличные,
М1 – деньги для сделок, включающие М0 + безналичные деньги (обналичиваемые депозиты, текущие счета, дорожные чеки), М1 предназначены для покупки товаров.
М2 – деньги в широком смысле. М2 = М1+ почти деньги (срочные вклады+счета денежного рынка, которыми оперируют банки, денежные фонды, другие почти деньги).
Самостоятельно почитать главу о происхождении денег в работе австрийского экономиста XIX века Карла Менгера: Менгер К. Основания политической экономии // Австрийская школа в политической экономии. – М.: Экономика, 1992. – Глава 8, за исключением третьего параграфа этой главы.
Снижение транзакционных издержек специализации происходит с появлением денег, решающих проблему двойного согласования желаний покупателя и продавца путем продажи в обмен на конкретный товар абстрактного товара-посредника –денег, который затем можно легко поменять на любой товар.
2.1. Сущность и функции денег
Деньги – это нечто, принимаемое как посредник обмена товара на товар: Т-Д-Т’
Определение денег вытекает из выполняемых ими функций. То, что выполняет функции денег, а именно: средства платежа (посредничества обмена), средство сохранения ценности, единицы учета благ, и называется деньгами.
а) Средство платежа или посредник обмена. Бартер – это прямой обмен товаров на товары без посредства денег. Требуются значительные усилия, чтобы найти покупателя вашего товара, который одновременно предложит нужный вам товар. Деньги как посредник легко разрешают проблему двойного согласования желаний покупателя и продавца. Деньги имеют ряд преимуществ перед другими средствами обмена: они легко делимы на части без потери ценности и портативны.
б) Средство сохранения ценности между сделками. Недостаток в том, что деньги, не имеющие внутренней ценности, обесцениваются при росте цен товаров. На ту же сумму денег можно меньше купить. От таких денег стараются избавиться. Поскольку так поступают все, то бегство от денег протекает бурно и ведет к быстрой потере ликвидности. Ликвидность – это свойство денег легко обмениваться. Все другие товары имеют ограниченную ликвидность – их сложнее продать. Деньги как товар обладают наибольшей среди них способностью к сбыту – ликвидностью. Именно вследствие меньшей ликвидности ценные бумаги называют денежными суррогатами. Например, вексель – обязательство оплатить долг (долговая расписка). Вексель можно продать другому лицу или банку, чтобы должник был должен уже не Вам, а им. Так вексель оказывается в вексельном обороте.
Деньги, которые выполняют функцию сохранения ценности (покупательную силу, покупательную способность) между сделками, одновременно ликвидны. Если есть опасность их обесценивания между сделками, то от таких денег все постараются избавиться, заменить твердой валютой, и никто не захочет их брать. Несохранение ценности ведет к неликвидности денег.
в) Единица учета. Для выражения цен товаров в стандартных единицах. Приспосабливание денег к инфляции называется индексацией. При высокой инфляции цены контрактов выражают в относительно стабильной иностранной валюте.
2.2. Декретные деньги
Два типа денег: 1) Имеющие внутреннюю ценность в каком-либо другом использовании. 2) Декретные деньги.
Скот и медь как деньги. В древнейшее время в Риме скот играл роль денег; об этом свидетельствует самое название последних pecunia (от pecus - скот); кроме того, по свидетельству источников, еще в начале периода республики имущественные штрафы назначались в виде известного количества скота. Позже они начинают употреблять металл, и именно медь, aes, откуда позднейшее выражение – aestimatio ["оценка"]. Первой чеканной монетой был as libralis – acc, равный 1 фунту меди.
Декретные (договорные) деньги. Они не имеют внутренней ценности. Стоимость их изготовления может быть в тысячи раз меньше, того, что на них написано и принимается рынком. Из-за опасности потери ликвидности и снижения покупательной силы в процессе инфляции декретные деньги не могут служить надежным средством накопления.
Декретные деньги принимаются населением как средство платежа потому, что правительство придает деньгам легальный статус, требуя оплаты ими налогов.
2.3. Измерение предложения денег
Широкий круг активов может выполнять функции денег. Поэтому трудно подвести черту и сказать: «Выше нее деньги, ниже нечто другое».
Измерение количества денег осуществляется в статистике с помощью денежных агрегатов.
Денежные агрегаты:
М0 – наличные,
М1 – деньги для сделок, включающие М0 + безналичные деньги (обналичиваемые депозиты, текущие счета, дорожные чеки), М1 предназначены для покупки товаров.
М2 – деньги в широком смысле. М2 = М1+ почти деньги (срочные вклады+счета денежного рынка, которыми оперируют банки, денежные фонды, другие почти деньги).
Самостоятельно почитать главу о происхождении денег в работе австрийского экономиста XIX века Карла Менгера: Менгер К. Основания политической экономии // Австрийская школа в политической экономии. – М.: Экономика, 1992. – Глава 8, за исключением третьего параграфа этой главы.
4. Русские учебники начала XIX века и их авторы
О вкладе Гурьева и его последователей и учеников мы уже говорили выше.
В 20-х годах XIX века появилось новое поколение уже самостоятельных русских учебников и учебных пособий по математике, авторами которых были Д.М. Перевощиков, Т.Ф. Осиповский и др.
Дмитрий Матвеевич Перевощиков (1788-1880) – русский астроном и математик. Родился в Пензенской губернии в дворянской семье, вместе с братом Василием, будущим писателем, философом и переводчиком, учился в Казанской гимназии. В 1808 стал одним из первых выпускников физико-математического факультета Казанского университета. Окончив его, начал работать старшим учителем математики в Симбирской гимназии (1809-1816).
В Симбирске он написал диссертацию о законе Ньютона, за которую в 1813 году получил от Казанского университета степень магистра. В 1818 г. был приглашён в московский университет, где преподавал сначала трансцендентальную геометрию, а затем все курсы астрономии, иногда (временно) прикладную математику и механику твердых и жидких тел. (с 1826 г. - профессор астрономии, 1833-1835 и 1836-1848 - декан отделения физических и математических наук, 1848-1851 – ректор университета). По его инициативе и под его руководством в 1830-1832 годах была построена Московская университетская обсерватория на Пресне, которую он возглавлял до 1851 г. В это же время (с 1820-х годов) им напечатано множество математических сочинений. Уйдя в отставку в 1851 г., поселился в Санкт-Петербурге, через год стал адъюнктом и работал в Петербургской Академии наук, а с 1855 г. - академиком АН.
По свидетельству современников, Д.М. Перевощиков был блестящим лектором – «преподавал математику вдохновенно, как поэт, как бы создавая её во время изложения, со страстной любовью к ней, которую сообщал и слушателям».
Хотя чисто ученые труды Дмитрия Матвеевича не внесли ничего существенно-ценного и нового в науку, тем не менее, его преподавательская деятельность, доставившая России многих известных математиков и воспитавшая несколько поколений, имеет громадное значение. Также Перевощиков известен как автор популярных в России учебников «Арифметика для начинающих» (1820), «Главные основания аналитической геометрии 3-х измерений» (1822), «Гимназический курс чистой математики» (1838), «Основания алгебры» (1854). Большую известность приобрела изданная в 1826-1837 гг. 13-томная «Ручная математическая энциклопедия», по которой, как говорили, «училась вся Россия», в частности М.Ю. Лермонтов, Н.В. Гоголь.
Так Гоголь в 1827 г. писал: «Не знаю, как воздать хвалу этому образцовому сочинению. Верите ли, что я, только читая её, понял всё то, что мне казалось тёмным, неудовлетворительным, когда проходил математику». М.Ю. Лермонтов также считал эту книгу одним из самых образцовых сочинений такого рода на русском языке.
Основные оригинальные исследования Перевощикова принадлежат астрономии, в основном - области небесной механики. Его труд «Вековые возмущения семи больших планет» (1859-1861) явился дальнейшим развитием классических исследований Ж. Л. Лагранжа и П. С. Лапласа. Вошёл в историю отечественной науки также как выдающийся популяризатор науки. Статьи Перевощикова по истории астрономии, которые печатались в журналах «Современник», «Отечественные записки» и других, сыграли большую роль в распространении научных знаний в России.
Большое значение имели проведенные Перевощиковым исследования научного наследия М. В. Ломоносова, особенно его работ по физике, атмосферному электричеству, географии. Перевощиков установил приоритет Ломоносова в открытии атмосферы Венеры и значение этого открытия для утверждения гелиоцентрического мировоззрения.
Тимофей Федорович Осиповский (1765-1832) – русский математик и философ-рационалист, учитель М. В. Остроградского. Родился в семье сельского священника, был отдан во Владимирскую семинарию, но незаурядные способности юного семинариста обратили на себя внимание его воспитателей. Пытливый ум, стремление всегда помочь другому разобраться в самых сложных вопросах и исключительная трудоспособность предвещали ему будущность учёного и педагога.
В 1783 году в Петербурге была учреждена первая в России учительская семинария, в которую были вызваны из духовных академий и семинарий лучшие студенты для подготовки к учительской деятельности, в том числе и Осиповский. В дальнейшем она была преобразована в Учительскую гимназию, в 1804 г. – в Педагогический, в 1816 г. – в Главный педагогический институт, в 1819 г. – в Петербургский университет. В качестве преподавателей сюда были приглашены академические профессора и адъюнкты, в том числе и непосредственные ученики Л. Эйлера. Изложение математики велось с подробными доказательствами и пояснениями, занятия проводились по лучшим учебным руководствам того времени, многие из которых принадлежали перу Л. Эйлера. Все это обеспечивало ученикам не только прочные знания по предмету, но и хорошую методическую подготовку.
По окончании семинарии Осиповский был сначала учителем физико-математических наук и русской словесности в Московском главном народном училище, а с 1800 по 1803 гг. - профессором математики Петербургской учительской гимназии, в которой он ранее учился. Он настолько выделялся яркими педагогическими способностями, общей эрудицией и глубокими познаниями в области физико-математических наук, что комиссия об учреждении училищ присылала ему на рецензию издаваемые ею математические сочинения. Однако деятельность Осиповского в этот период не ограничивалась только преподаванием, он работал над составлением и изданием собственного учебника по математике. По замыслу автора здесь должен быть представлен обширный по материалу, связанный единством и последовательностью изложения курс, по которому учащийся мог получить полное университетское математическое образование, во многих разделах даже превышавшее требования тогдашней университетской программы.
Осиповский выполнил свой замысел и написал новый «Курс математики», пользовавшийся в свое время большой известностью и выдержавший три издания. Это руководство полнее, чем все тогда принятые для преподавания в гимназиях, освещало математические знания того времени, начиная от элементарных, начальных сведений по арифметике и кончая вариационным исчислением. Глубокое содержание, строгая научная последовательность, новизна в освещении многих вопросов обеспечили этому курсу заслуженную репутацию одного из лучших руководств того времени по дифференциальному и интегральному исчислению.
В конце 1802 г. Осиповский дал согласие на назначение его профессором математики в Харьковский университет, и в 1803 г., еще до открытия университета (официально он был открыт в 1805 г.) переехал в Харьков. В течение первого десятилетия существования Харьковского университета он преподавал практически все математические дисциплины: геометрию, дифференциальное, интегральное и вариационное исчисления, приложения аналитических функций к высшей геометрии. Благодаря Осиповскому Харьковский университет с самого начала занял ведущее место по постановке преподавания математических дисциплин, наряду с Дерптским и Казанским.
С 1813 по 1820 г. Осиповский исполнял обязанности ректора Харьковского университета. Он инициировал создание при Харьковском университете Общества наук, целью которого было распространение знаний на Юге России. По «Курсу математики» Осиповского, переработанному к тому времени и переизданному в 3-х томах, успешно велось преподавание математики в Харьковском университете всю первую четверть XIX столетия. О содержании 3-ей присоединённой части можно получить некоторое представление из отзыва Н.И. Фусса (1810). Фусс писал, что третий том курса высшей математики Осиповского
«заключает в себе отвлеченные исследования, значительно превышающие даже и тот курс чистой математики, который преподается в университетах… Его можно обратить к тому только малому количеству учеников, которые математику во всей обширности избрали главным предметом своего учения, в особенности же для тех, кто не знает иностранного языка, ибо, сколько известно, нет еще на русском языке такого сочинения, в котором бы так пространно, как тут, рассуждалось бы о приложении теории функций к кривым линиям и поверхностям».
Таким образом, вторая часть третьего тома содержала изложение дифференциальной геометрии. Этот раздел непременно входил в курс лекций, читавшихся Осиповским на втором курсе по 4 часа в неделю.
За время своей педагогической деятельности Осиповский воспитал многих учеников, среди которых были знаменитый Остроградский и профессор Харьковского университета Павловский.
Андрей Федорович Павловский (1788–1856) - профессор математики и ректор Харьковского университета (1780 - 1789). Родился он в семье небогатого помещика, с 1806 по 1809 г. учился в только что открытом Харьковском университете по физико-математическому факультету под руководством известного математика Осиповского, а затем на протяжении 40 лет преподавал там же различные математические дисциплины. В 1816 г. он был произведен в адъюнкты, тремя годами позже утвержден в звании экстраординарного профессора, а впоследствии и ординарного профессора (1826).
В 1810 г. Осиповский передал Павловскому преподавание элементарной математики на первом курсе, а с 1815 г – и преподавание первых разделов высшей математики: теории конечных разностей и дифференциального исчисления. После увольнения Осиповского (в 1820 г.) Павловский на протяжении многих лет вел весь курс высшей математики, в том числе и приложения дифференциального исчисления к высшей геометрии, по собственным тетрадям, следуя Эйлеру, Лагранжу и Монжу.
Павловский писал мало, т.к. многочисленные обязанности отвлекали его от науки. Известно в печати только два его труда: актовая речь 1821 г. о вероятности и логарифмические таблицы Каллета (1820). Но это был профессор по призванию, горячо преданный своей науке, университету и студентам, великолепно читал лекции и обладал большой математической эрудицией. Ему принадлежит заслуга в воспитании молодого Остроградского. Благодаря Осиповскому и Павловскому семнадцатилетний Остроградский в 1818 г. впервые серьезно заинтересовался математикой. В конце 80-х годов в Харьковском университете при физико-математическом факультете на средства сына его, Федора Андреевича Павловского, учреждена премия А.Ф. Павловского за лучшие сочинения по математике.
5. Математика первой половины XIX века в лицах
Имя Н.И. Лобачевского – великого русского математика, «Коперника геометрии» – известно многим, прежде всего как создателя неевклидовой геометрии. Его мысли и деяния в области математического образования менее известны, хотя и достаточно значимы.
Николай Иванович Лобачевский (1792-1856) родилсяв Нижнем Новгороде в бедной семье мелкого чиновника (есть другие версии). Девятилетним мальчиком он был привезен матерью в Казань и ее стараниями устроен вместе с двумя братьями в гимназию на казенное содержание. В гимназии («Воспоминания» С.Т. Аксакова) увлекательно преподавал математику талантливый учитель Г.И. Карташевский, воспитанник Московского университета, поставивший изучение математики на значительную высоту. И когда юный 14-летний Лобачевский становится в феврале 1807 года студентом университета (тоже казеннокоштным), он уже вскоре проявляет особенную склонность к изучению физико-математических наук, обнаруживая выдающиеся способности. В этом, несомненно, сказались результаты педагогической деятельности у его учителя
Однако в университете Лобачевскому уже не удалось слушать лекции Карташевского, так как последний в декабре 1806 г. был отстранен от должности директором И.Ф. Яковкиным, как «проявивший дух неповиновения и несогласия». Математические курсы в университете стал вести М.Ф. Бартельс, прибывший в Казань в 1808 году. Успехи студента Лобачевского, соревнующегося в своих занятиях с Симоновым, впоследствии известным астрономом и участником кругосветного плавания, неизменно вызывали одобрение М.Ф. Бартельса и других профессоров.
В 1811 г. Лобачевский, минуя степень кандидата, утверждается магистром. После окончания университета он был оставлен в нём для преподавания: с 1814 г. – адъюнкт по математике, с 1816 г. – профессор.
Его руководитель профессор Бартельс - квалифицированный математик, опытный преподаватель, но не ведущий творческой работы. Под его руководством Лобачевский изучил классические труды по математики и механике: «Теорию чисел» Гаусса и первые тома «Небесной механики» Лапласа. В результате он представил два научных исследования:
ü по механике «Теория эллиптического движения небесных тел» (1812),
ü по алгебре «О разрешимости алгебраического уравнения xn - 1 = 0» (1813),
и был ранее срока в 1814 г. произведен в адъюнкт-профессоры (доценты).
Несмотря на тысячи текущих дел и обязанностей, Лобачевский занимается напряженной творческой деятельностью:
· пишет два учебника для гимназий: «Геометрию» (1823 г.) и «Алгебру» (1825 г.). "Геометрия" получает отрицательный отзыв у академика Н.И. Фусса, не оценившего тех изменений, который Лобачевский внес в традиционное изложение, и осудившего введение метрической системы мер, поскольку она создана в революционной Франции. "Алгебра" из-за внутренних проволочек в университете тоже не была напечатана.
· неустанно развивает и шлифует главное дело своей жизни - неевклидову геометрию. В докладе «Сжатое изложение начал геометрии» от 23 февраля 1826 г. – первый набросок теории (дата считается днём рождения неевклидовой геометрии). Рукопись доклада до нас не дошла, а материал был включен автором в его первое сочинение «О началах геометрии» (1829 – 1830).
Принципиально критический пересмотр самых первых, начальных, геометрических понятий, принятых в геометрии еще со времен Евклида (3 век до н.э.) позволил Лобачевскому сделать ему это выдающееся открытие. Избранное им направление исследований способствовало тому, что он не только в геометрии, но и в ряде других областей математики превосходит достигнутый в то время уровень науки:
· им дано уточнение понятия функции, приписанное впоследствии Дирихле;
· четко разграничены непрерывность функции и ее дифференцируемость;
· проведены глубокие исследования по тригонометрическим рядам, опередившие его эпоху на много десятилетий;
· разработан метод численного решения уравнений, несправедливо получивший впоследствии название метода Греффе, тогда как Лобачевский и независимо от него бельгийский математик Данделен разработали этот метод значительно раньше.
В течение более чем 30 лет, до 1846 г., он читал все основные курсы по математике. В 1827 г. его избрали ректором, и 19 лет он самоотверженно трудился на этом посту, добиваясь расцвета Казанского университета. Лобачевский стремился претворить в жизнь свою широкую передовую программу университетского образования, представление о которой дает его речь «О важнейших предметах воспитания», произнесенная им через год после назначения ректором.
Продолжая геометрические исследования, Лобачевский публикует работу за работой:
· 1829-1830 гг. - «О началах геометрии»,
· 1835 г. - «Воображаемая геометрия»,
· 1836 г. - «Применение воображаемой геометрии к некоторым интегралам»,
· 1835-1838 гг. - обширная работа «Новые начала геометрии с полной теорией параллельных»,
· 1840 г. - на немецком языке «Геометрические исследования по теории параллельных», где содержится предельно ясное и лаконичное изложение его основных идей.
Эта мужественная борьба за научную истину резко отличает Лобачевского от других современников, приближавшихся тоже к открытию неевклидовой геометрии. Но научные идеи Лобачевского не были поняты современниками. Его труд «О началах геометрии», представленный в 1832 году советом университета в Академию наук, получил у М. В. Остроградского отрицательную оценку. В иронически-язвительном отзыве на книгу Остроградский откровенно признался, что он ничего в ней не понял, кроме двух интегралов, один из которых, по его мнению, был вычислен неверно (на самом деле ошибся сам Остроградский). Среди других коллег также почти никто Лобачевского не поддержал, росли непонимание и невежественные насмешки. Венцом травли стал издевательский анонимный пасквиль (подписанный псевдонимом С. С.), появившийся в журнале Ф. Булгарина «Сын отечества» (1834).
Непонимание значения его новой геометрии, жестокая неблагодарность современников, материальные невзгоды, семейное несчастье и, наконец, слепота не сломили его мужественного духа. За год до смерти он закончил свой последний труд «Пангеометрия», диктуя его своим ученикам.
Михаилу Васильевичу Остроградскому в истории русской математики принадлежит одно из наиболее почётных мест. Острый и смелый ум, широкое математическое образование и хорошее знание современного ему естествознания позволили ему получить результаты первостепенного значения в механике и различных частях математики. Результаты многих его научных исследований вошли в учебники, но многие его крупнейшие достижения, как это часто случалось с работами русских учёных, остались неизвестными широким научным кругам Запада и позднее были заново получены другими исследователями. Однако, несмотря на то, что лишь относительно небольшая часть его исследований стала достоянием современной ему европейской науки, его имя получило широкое признание далеко за пределами родины. М. В. Остроградский был избран академиком не только Российской, но также Туринской, Римской, Американской академий и членом-корреспондентом в то время наиболее сильной по составу и научному весу Парижской академии наук. О том, как велика была слава М. В. Остроградского в России, можно судить хотя бы по тому, что когда молодые люди отправлялись, учиться в высшие учебные заведения, то друзья и родные напутствовали, их словами "становись Остроградским".
Михаил Васильевич Остроградский (1801–1862) – один из величайших русских математиков рассматриваемой эпохи. Родился в семье помещика Полтавской губернии, учился при Полтавской гимназии в "Доме для воспитания бедных дворян", но гимназического курса обучения не закончил и, по желанию отца, вышел из 3-го класса гимназии. Отец хотел видеть сына военным; это было в то же время сильнейшим желанием мальчика. В 1816 г. М. В. Остроградского повезли в Петербург для зачисления в один из гвардейских полков, но не довезли туда, круто изменив решение по совету одного из родственников, горячо настаивавшего на определении юноши в университет. Это решило его дальнейшую судьбу. В 1817 г. его приняли в Харьковский университет.
М. В. Остроградский ещё долго мечтал о военной службе и учился плохо. Лишь в конце второго года, университетской жизни образ его мыслей резко изменился; он начал работать и сразу же ощутил в себе призвание к математике. Поводом для этого послужило то обстоятельство, что он перешёл жить на квартиру университетского преподавателя математики Павловского. Последний своими беседами сумел пробудить сначала интерес, а затем и страстную любовь М. В. Остроградского к науке. С жаром принявшись за учение, М. В. Остроградский через два месяца поражал Павловского своими успехами. Математический талант давал М. В. Остроградскому возможность налету схватить прочитанное и подмечать промахи и ошибки изложения.
В 1820 г. М. В. Остроградский захотел оформить окончание университета. Для этого следовало сдать экзамены. Он их с блеском сдал. Ректор университета Осиповский, просвещённый и деятельный профессор, предложил присудить М. В. Остроградскому первую учёную степень кандидата. Однако острая политическая борьба, существовавшая среди харьковской профессуры, привела к тому, что её реакционная часть добилась лишения М. В. Остроградского диплома об окончании университета, мотивируя это его вольнодумством и непосещением лекций по богослужению. Так он и не закончил Харьковский университет.
Эта обида не обескуражила М. В. Остроградского, а скорее побудила его к дальнейшей настойчивой работе. В 1822 г. он отправился в Париж и там с жадностью начал впитывать высокую послереволюционную культуру французской математической школы, слушая лекции выдающихся математиков и физиков того времени: Ампера, Коши, Лапласа, Пуассона, Фурье. Вскоре он начал пробовать свои силы и на пути самостоятельного творчества. Уже в 1825 г. Коши в одном из мемуаров с похвалой отзывается об исследованиях М. В. Остроградского, посвящённых вычислению интегралов. В следующем году М. В. Остроградский представил Парижской академии свой первый мемуар " О волнообразном движении жидкости в цилиндрическом сосуде ". Впоследствии он был напечатан в её трудах. В этом мемуаре М. В. Остроградский с большим искусством устанавливает общие выражения для скоростей тяжёлой жидкости в цилиндрическом сосуде и указывает способ определения этих скоростей по начальному виду свободной поверхности и начальным значениям скоростей.
М. В. Остроградскому пришлось заниматься не только научной работой. Денежные затруднения заставили его преподавать в колледже Генриха IV, куда он поступил по рекомендации своих учителей.
В ноябре 1827 г. М. В. Остроградский вернулся в Россию. Сохранились документы, указывающие на то, что тотчас же по возвращении в Петербург он был взят под надзор полиции. Однако репутация талантливого учёного, приобретённая М. В. Остроградским в Париже, раньше него донеслась в Россию и доставила ему, вскоре по приезде в Петербург, звание адъюнкта Академии наук, а в 1830 г. звание экстраординарного и через год ординарного академика по прикладной математике.
В Петербурге М. В. Остроградский продолжал свои научные изыскания и со страстью отдался педагогической работе. Он преподавал в Педагогическом институте, в Институте инженеров путей сообщения, в Морском корпусе, в Михайловской артиллерийской академии, долгое время был главным наблюдателем за преподаванием математики в кадетских корпусах.
В своей педагогической деятельности М. В. Остроградский всегда стремился познакомить слушателя с последними достижениями математической науки. Так, например, в Институте инженеров путей сообщения он рассказывал о работах Абеля по алгебраическим функциям, об исследованиях Штурма относительно отделения корней алгебраических уравнений (теорема Штурма) и других результатах научной деятельности зарубежных математиков. Уровень преподавания М. В. Остроградского в технических учебных заведениях был значительно выше уровня преподавания в университетах, где готовились специалисты-математики. Это не могло пройти бесследно. И действительно, многие ученики М. В. Остроградского сами впоследствии стали профессорами университетов, технических и военных учебных заведений.
Предметом исследований М. В. Остроградского были: математическая физика, аналитическая и небесная механика, а также смежные с математикой области. И он с одинаковым успехом работал во всех этих областях, часто опережая своих европейских коллег.
С особенной любовью занимался он аналитической механикой, к которой относится большинство его учёных работ. Наряду с общими проблемами механики, он дал решения многих частных механических задач в области гидростатики, гидродинамики, теории упругости, теории притяжения и баллистики.
М. В. Остроградский:
· установил, независимо от английского учёного Гамильтона, один из важнейших законов механики, так называемый принцип наименьшего действия;
· сформулировал в наиболее общем виде начало возможных перемещений, устранив в работах Лагранжа, создателя этого предложения, ненужные ограничения и исправив допущенные этим последним ошибки в выводе уравнений динамики;
· опубликовал мемуар о вычислении вариаций кратких интегралов (1834), который появился в 1861 г. в полном переводе как приложение к книге английского математика и историка математики Тотгентера, посвященной истории развития вариационного исчисления;
Кстати, в 1840 г. Парижская академия наук объявила премию за решение проблемы, уже решённой за 6 лет до этого М. В. Остроградским в указанном мемуаре, и присудила её французскому математику Саррюсу за сочинение, содержавшее ошибочные заключения.
· дал важнейшую формулу кратного интегрирования, позволяющую вычисление n-кратного интеграла сводить к вычислению (n-1)-кратного. Эта формула Остроградского в частном случае при n = 3 известна каждому изучавшему курс математического анализа или математической физики.
Исследования М. В. Остроградского по математической физике касаются весьма разнообразных вопросов: распространения тепла, распространения волн на поверхности жидкости, теории удара, уравнений движения упругого тела. Здесь, как и всюду, следуя складу своего ума, он стремится к получению наиболее общих результатов и даёт широкие обобщения.
Несколько работ М. В. Остроградского посвящено баллистике. Эти работы, а также исследования по небесной механике, привели его к работе в области приближённых вычислений, где им даны важные формулы. Значительный интерес М. В. Остроградский проявил к теории алгебраических функций и опубликовал в этом направлении ряд своих исследований. Он нашёл метод выделения алгебраической части интеграла от рациональной функции, приводимый теперь в учебниках.
Три работы М. В. Остроградского посвящены теории вероятностей. Во введении к одной из них М. В. Остроградский говорит, что она может иметь практическое применение при браковке принимаемых материалов. Это замечание характерно для всей деятельности М. В. Остроградского, который привык считать, что прогресс теоретической науки неразрывно связан с приложениями её результатов к практике.
Уже простое перечисление тем проведённых М. В. Остроградским исследований обнаруживает исключительную разносторонность его интересов и творческих способностей. В 1856 г. Парижская академия наук избрала М. В. Остроградского своим членом-корреспондентом в награду за его научные заслуги. Научные связи, завязанные им в Париже, он сохранил до последних дней жизни, состоя, например, в дружеской переписке с Коши до самой его смерти.
В развитие математической культуры в России М. В. Остроградский внёс такой вклад, значение которого трудно переоценить. Своими публичными лекциями М. В. Остроградский способствовал приобщению русской интеллигенции к высоким идеям науки. Лекции М. В. Остроградский читал просто и ясно. При изложении сложных и трудных мест, заметив, что у слушателей встречаются затруднения, он немедленно предлагал иное доказательство, часто импровизируя его тут же у доски. Прочитанные им в 1836-1837 гг. публичные лекции по высшей алгебре и напечатанные под названием " Лекции алгебраического анализа " пользовались большим успехом. В лекциях по небесной механике, прочитанных в заседаниях Академии наук в течение нескольких месяцев, он не только изложил состояние этой науки, но и улучшил самое изложение, наполнив этот курс, как своими доказательствами ряда предложений, так и более принципиальными идеями.
Для характеристики М. В. Остроградского как педагога следует отметить, что способных студентов он поощрял к занятиям, но для слабых и бездарных он был грозой. На экзаменах эти последние прятались, под предлогом болезни ложились в лазарет и откладывали экзамены до более подходящего случая.
М. В. Остроградский интересовался также преподаванием элементарной математики. С целью его улучшения им:
· написан «Конспект по тригонометрии», в котором впервые в учебной литературе дано определение тригонометрических величин исходя из соотношения сторон прямоугольного треугольника – это важный методический приём изучения начал тригонометрии;
· издан учебник «Руководство начальной геометрии», в котором предпринята попытка изложения геометрии в возможно более тесной связи с алгеброй, т.е. более широко использованы аналитические приёмы доказательства. Учебник не нашёл широкого применения, т.к. оказался слишком сложным для учащихся и ненаглядным, оторванным от практики, причём, несмотря на то, что сам автор неоднократно говорил о пользе наглядности и практической направленности математики!?
· совместно с проф. Блюмом опубликована брошюра о преподавании математики в школе;
· создана особая математическая комиссия для окончательного суждения о качестве учебников по математике для средних специальных учебных заведений (В.Я. Буняковский, П.Л. Чебышев, Д.И. Перевощиков, О.И. Сомов, П.И. Лавров).
Остроградский строго подходил к отбору преподавателей математики для военных учебных заведений: каждому кандидату необходимо было сдать ему экзамен и прочитать пробную лекцию на тему, избранную самим Остроградским.
Остроградский считал полезным введение в программу средней школы элементов высшей математики, в 1850 г. он сумел это сделать практически: во всех четырёх общих классах кадетских корпусов стали изучать начала высшей математики.
Большое значение в обучении придавал Остроградский:
ü связи с физикой и естествознанием,
ü историзму,
ü повторению,
ü воспитанию познавательного интереса.
«Заинтересовать ум ребёнка – вот что является одним из главных пунктов нашей доктрины, и мы не пренебрегаем ничем, чтобы привить ученику вкус – мы бы сказали даже – страсть к учёбе».
О лекциях.
Лекции Остроградского по геометрии записал один из студентов Главного педагогического института Николай Сергеевич Будаев (1833–1902), слушавший их в 1851–1852 г. В 1853 г. Будаев окончил с золотой медалью Главный педагогический институт и был оставлен в том же институте адъюнктом физико-математического факультета. Впоследствии он стал заслуженным профессором математики Петербургского университета и Михайловской артиллерийской академии и училища. Указанные лекции Остроградского были посвящены приложениям анализа к геометрии. Они оставались в рукописи и только в XX в. перед началом Великой Отечественной войны были подготовлены к печати Алексеем Николаевичем Крыловым (1863–1945). Но, к сожалению, в годы войны набор текста лекций и другие связанные с ним материалы пропали. Об этих лекциях А.Н. Крылов сделал специальный доклад Президиуму АН СССР. Он отмечал, что лекции М.В. Остроградского начинались с учения о касательных и кривизне линий в пространстве; плоские кривые рассматривались как частный случай пространственных. Далее шли исследования кривизны поверхностей и линии кривизны. С помощью вариационного исчисления было изложено учение о геодезических линиях. По словам А.Н. Крылова, эти лекции отличаются значительными методическими достоинствами и содержат большое число примеров, решенных различными методами; изложение оживляется историческими замечаниями.
Представление о лекциях Остроградского по приложениям дифференциального исчисления к геометрии, которые он читал в Главном инженерном училище, можно получить, ознакомившись с «Курсом дифференциального исчисления» (1849 г.), составленным одним из его слушателей инженером-прапорщиком Виктором Ивановичем Беренсом (1814–1884). Все приложения дифференциального исчисления к геометрии собраны в отдельный раздел, который состоит из шести глав. Первые три из них (с XVII по XIX) посвящены теории кривых на плоскости; следующие две главы (XX и XXI) – теории кривых в пространстве; и, наконец, последняя XXII глава – общей теории соприкасания поверхностей. Таким образом, лекции Остроградского охватывали все разделы дифференциальной геометрии того времени.
в) В.Я Буняковский.
Виктор Яковлевич Буняковский (1804-1889) родился в Подольской губернии в семье офицера. Отец его служил подполковником конно-польского уланского полка и погиб в 1809 году в Финляндии. Первоначальное образование получил в Москве, в доме друга его отца, графа А. П. Тормасова. В 1820 году Буняковский, вместе с сыном графа, отправился за границу, где изучал преимущественно математические науки, слушал лекции в Сорбонне. Он имел возможность заниматься у Лапласа, Пуассона, Фурье, Коши, Ампера, Лежандра и других знаменитых учёных. Здесь же, в Париже, он познакомился с Остроградским, с которым впоследствии дружно работал. В 1825 г. Буняковский защитил диссертацию, состоящую из 2 работ (по аналитической механике «Об одном случае вращательного движения в сопротивляющейся среде» и к математической физике «О распространении тепла внутри твердых тел», получив от парижского факультета наук степень доктора математических наук.
Пробыв за границей в общей сложности семь лет, Буняковский в 1826 году приехал в Петербург, где занялся педагогической деятельностью. Сначала преподавал математику в 1-ом кадетском корпусе (1827), затем - в Морском корпусе, где проработал 36 лет, и в Институте путей сообщения (1830-1846). Прекратив преподавание в корпусе, Буняковский в течение длительного периода не прерывал своей связи с военными учебными заведениями, выполняя разные поручения программно-методического характера. Кроме того, с 1846 по 1860 гг. он являлся профессором Петербургского университета, читал лекции по различным разделам математического анализа, теории вероятностей, аналитической механики и др. С 1858 г был главным экспертом правительства по вопросам статистики и страхования.
В университете В. Я. Буняковский читал курсы:
· аналитической механики (по Остроградскому и Пуассону),
· дифференциального и интегрального исчислений (по Коши),
· теории вероятностей (собственный оригинальный курс),
· интегрирования дифференциальных уравнений, вариационного исчисления, исчисления конечных разностей.
С 1828 г избран адъюнктом, а в 1830 г. – академиком ПАН, с 1864 г. в течение 25 лет состоял вице-президентом АН. Список сочинений Буняковского насчитывает 168 наименований: преимущественно это труды по теории чисел и теории вероятностей с её приложениями, а также работы, посвящённые вопросам анализа, геометрии и алгебры.
Важнейшее место в исследованиях Буняковского занимают труды по теории вероятностей. Знаменитые «Основания математической теории вероятностей» (1846) - обширный трактат, послуживший началом его всемирной известности.
Кроме теории, в трактате
· изложение истории возникновения и развития теория вероятностей;
· в нём впервые сведено вместе всё то, что было выработано по этой теории трудами известных математиков, начиная с Паскаля и Ферма,
· даны объяснения относительно новых решений самых трудных и запутанных вопросов,
· указано много практических приложений теории вероятностей:
ü к вопросу о средней продолжительности жизни людей различных возрастов,
ü к определению достоверности свидетельств и преданий,
ü к вспомогательным кассам и страховым учреждениям,
ü к определению погрешностей при наблюдениях, к вопросам судебного дела,
ü к вычислению вероятностных потерь в войске и т. д.
Форма «Оснований математической теории вероятностей» отличались такой удобопонятностью и изяществом, что Гаусс и Биенеме (итальянский скульптор) выучились русскому языку по этому сочинению. Ряд позднейших его статей посвящён статистике народонаселения, подсчёту вероятных контингентов русской армии, задачам судопроизводства, определению погрешности наблюдений («О возможности введения определённых мер доверия к результатам некоторых наук и преимущественно статистики» (1846) и даже «Геометрические соображения по наивыгоднейшим расположениям громоотводов» (1863)). Все эти работы способствовали развитию теории вероятностей в России.
Работы по теории чисел о сравнениях, квадратичном законе взаимности и др. возродили в русской науке интерес к теории чисел, успешно разрабатывавшейся в Петербургской АН в XVIII веке. В исследованиях Буняковского в области теории чисел видны непосредственная преемственность с трудами Эйлера, прекрасное знание работ Лежандра и Гаусса.
В математическом анализе наибольшее значение имеет открытое Буняковским неравенство Шварца, хотя Шварц нашёл его на 10 лет позднее Буняковского (в 1875 г.):
.
Наряду с Остроградским, Буняковский сыграл огромную роль в повышении научного уровня преподавания математики в высшей школе и расширении её учебной программы. Ратуя за чёткость и однозначность математической терминологии, он составил «Лексикон чистой и прикладной математики» (до буквы Е), дававший обширные материалы для изучения разных частных математических вопросов. Цель издания «Лексикона», с одной стороны, дать русским читателям «достаточные сведения обо всех важнейших теориях, как старых, так и новейших», с другой - обогатить русскую математическую терминологию, весьма неполную тогда во многих отношениях. Слова в этом «Лексиконе» расположены по французскому алфавиту, с переводом на русский язык, а также с подробным объяснением на русском языке значения каждого термина. Уже после смерти Буняковского в его бумагах была найдена рукопись под заглавием: «Наброски для математического лексикона Буняковского, буквы E, F, G, H, I, J, K, L», с надписью рукой Буняковского: «Не печатать, а передать в архив академии наук, как пособие для справок продолжателям моего математического Лексикона». Эта рукопись сохраняется в отделе рукописей II отделения библиотеки академии.
Для средней школы им написаны два учебника: «Арифметика» (1844) и «Программа и конспект арифметики» (1849). Первый из них был рекомендован Учёным комитетом для гимназий, использовался в большинстве округов России и выдержал два издания
Буняковский, кроме того, был изобретателем (планиметр, пантограф, прибор для измерения квадратов и самосчеты). В Политехническом музее в Москве хранятся его самосчеты, о чем свидетельствует приложенная записка: «Самосчеты академика В.Я. Буняковского. Подарены Музею вдовой его Екатериной Николаевной через непременного члена Императорского Общества любителей Естествознания и Астрономии Владимира Георгиевича фон-Бооль». Из-за своих недостатков самосчеты распространения не получили. Но вскоре был изготовлен компактный прибор, который является видоизмененными самосчетами Буняковского. Этот прибор был обнаружен в 70-х годах прошлого столетия.
Его близкими друзьями были М.В. Остроградский, П.Л. Чебышев, О.И. Сомов и др. Научные заслуги Буняковского были оценены уже современниками. Он был почётным членом всех русских университетов, многих иностранных и русских учебных обществ. При академии наук была учреждена премия его имени за лучшие сочинения по математике. Буняковский пользовался заслуженным авторитетом среди европейских учёных.
При богатстве и глубине содержания, лекции Буняковского всегда отличались поразительной ясностью, увлекательностью и в то же время литературной красотой изложения, делали легко доступными самые сложные математические положения и увлекали даже безучастных слушателей. По отношениям к лекциям Буняковский проявлял замечательную аккуратность и в течение всего времени своей службы в университете не пропустил ни одной лекции и не опоздал ни разу.
Как человек, Буняковский отличался высокими нравственными качествами, и уважение, которым он пользовался, имело причины не только его громкой славы великого учёного, но и в личных достоинствах. Одарённый чувством изящного, Буняковский в молодости увлекался поэзией Байрона, перевёл отрывок из «Чайльд-Гарольда», и несколько стихотворений помещённых им в журналах сороковых годов.
В. А. Панаев, ученик Буняковского по Петербургскому институту путей сообщения, в своих «Воспоминаниях», напечатанных в «Русской старине» за ноябрь 1893 г., писал: " профессорами из предметов высшей математики были академики: гениальный Остроградский и талантливейший, с беспримерной эрудицией, знаменитый Буняковский... Ни для кого не может быть сомнения, что В. Я. Буняковский одарен великими и быстрыми способностями, необычайным талантом и по своим трудам может быть причислен к гигантам науки ".
Химическая – представлена разными отраслями. Горно-химическая – добыча фосфоритов. Производство минеральных удобрений - Новгород (азотные), Волхов (фосфорные). Полимерная химия – Санкт-Петербург (пластмассы, резино-технические изделия). Полимерная химия основана на привозном сырье, отходах Киришского НПЗ.
Лесная промышленность – представлена деревообработкой и целлюлозно-бумажной. Своего сырья не хватает, получает древесину из Северного района. Крупные ЦБК по производству бумаги и картона находятся в Ленинградской области (на Карельском перешейке) – Приозерский, Светлогорский, Советский комбинаты дают более 10% общероссийской продукции.
Легкая промышленность – характеризуется высокой концентрацией в Санкт-Петербурге. Преобладают такие отрасли как трикотажная, обувная, нитяная, швейная.
Сельское хозяйство – играет второстепенную роль в экономике района. Причины этого кроются в природно-климатических условиях и особенностях развития района. Сельское хозяйство отличается своим пригородным типом. Отраслями специализации Северо-Западного района являются льноводство и молочно-мясное скотоводство.В земледелии примерно половина посевов приходится на зерновые культуры - рожь, ячмень, овес. Кормовые культуры, картофель занимают значительные площади. В Псковской и Новгородской областях выращивают лен-долгунец.
Животноводство является ведущей отраслью сельского хозяйства, оно дает 60-70% сельскохозяйственной продукции района. Развитию животноводства способствует устойчивая кормовая база, представленная естественными пастбищами и сенокосами, а также посевами кормовых культур. Животноводство имеет в основном пригородный тип. Преобладает скотоводство молочного и молочно-мясного направления. Развиты свиноводство, птицеводство и пушное звероводство.
Центрально-Черноземный экономический район.
Центрально-Черноземный экономический район включает в свой состав Белгородскую, Воронежскую, Курскую, Липецкую и Тамбовскую области.
Территория – 167,7 тыс. км. Кв.Население – 8 млн. человек.
Район не обладает мощным экономическим потенциалом и находится на одном из последних мест по многим показателям: численности населения, производственным фондам, производимой промышленной продукции. Главные его особенности:
- наличие КМА (самая большая железорудная база страны);
- одна из основных продовольственных баз страны.
Район имеет выгодное ЭГП. Граничит с Центральным районом, Поволжьем. Его территорию пересекают потоки сырья, топлива и энергии. имеет развитую сеть железных и автомобильных дорог. Общая конфигурация дорог сложилась еще до революции и напоминает решетку. Территорию района пересекают меридиональные и широтные магистрали межрайонного значения.
Природно-ресурсный потенциал.
Центрально-Черноземный район занимает южную часть Среднерусской возвышенности и часть Окско-Донской равнины. Климат умеренно-континентальный. Средняя температура января от (-8 до –11), июля - + 19-20. Продолжительность периода активной вегетации – 140-170 дней. Годовая сумма осадков составляет 400-500 мм. Район относится к зоне неустойчивого увлажнения, подвержен засухам. Большая часть района находится в лесостепной зоне, которая постепенно переходит в степную. Гидрографическая сеть бедная, единственная крупная река – Дон, остальные реки мелководны и используются только для водоснабжения.
Зональные типы почв – черноземы. Только на северо-западе и северо-востоке района серые лесные почвы. Мощность гумусового горизонта примерно 120 см, содержание гумуса – от 4 до 10%. Проблемой является подверженность почв к эрозионным процессам.
Основным богатством района являются железные руды КМА, открытой еще в 1783 году, но добыча руды началась только в 20 веке. Площадь железорудного района КМА охватывает 120 тысяч км. Кв. В основном это Курская и Белгородская области. 90 % запасов руд КМА находятся на территории Белгородской области. Крупнейшие месторождения – Лебединское, Стойленское, Коробковское (Белгородская) и Михайловское. Из других минераль
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 398; Нарушение авторских прав?; Мы поможем в написании вашей работы!