Алгоритмы электронной цифровой подписи

Технология применения системы ЭЦП предполагает наличие сети абонентов, посылающих друг другу подписанные электронные документы. Для каждого абонента генерируется пара ключей: секретный и открытый. Секретный ключ хранится абонентом в тайне и используется им для формирования ЭЦП. Открытый ключ известен всем другим пользователям и предназначен для проверки ЭЦП получателем подписанного электронного документа. Иначе говоря, открытый ключ является необходимым инструментом, позволяющим проверить подлинность электронного документа и автора подписи. Открытый ключ не позволяет вычислить секретный ключ.

Для генерации пары ключей (секретного и открытого) в алгоритмах ЭЦП, как и в асимметричных системах шифрования, используются разные математические схемы, основанные на применении однонаправленных функций. Эти схемы разделяются на две группы. В основе такого разделения лежат известные сложные вычислительные задачи:

· задача факторизации (разложения на множители) больших целых чисел;

· задача дискретного логарифмирования.

Алгоритм цифровой подписи RSA

Первой и наиболее известной во всем мире конкретной системой ЭЦП стала система RSA, математическая схема которой была разработана в 1977 г. в Массачуссетском технологическом институте США.

Сначала необходимо вычислить пару ключей (секретный ключ и открытый ключ). Для этого отправитель (автор) электронных документов вычисляет два больших простых числа P и Q, затем находит их произведение

N = P * Q

и значение функции

j (N) = (P –1)(Q –1).

Далее отправитель вычисляет число E из условий:

E £ j (N), НОД (E, j (N)) =1

и число D из условий:

D < N, E * D º1 (mod j (N)).

Пара чисел (E,N) является открытым ключом. Эту пару чисел автор передает партнерам по переписке для проверки его цифровых подписей. Число D сохраняется автором как секретный ключ для подписывания.

Обобщенная схема формирования и проверки цифровой подписи RSA показана на рис.6.4.

Допустим, что отправитель хочет подписать сообщение M перед его отправкой. Сначала сообщение M (блок информации, файл, таблица) сжимают с помощью хэш-функции h(·) в целое число m:

m = h(M).

Затем вычисляют цифровую подпись S под электронным документом M, используя хэш-значение m и секретный ключ D:

S = m^D (mod N).

Пара (M,S) передается партнеру-получателю как электронный документ M, подписанный цифровой подписью S, причем подпись S сформирована обладателем секретного ключа D.

После приема пары (M,S) получатель вычисляет хэш-значение сообщения M двумя разными способами. Прежде всего, он восстанавливает хэш-значение m´, применяя криптографическое преобразование подписи S с использованием открытого ключа E:

m´ = S^E (mod N).

Кроме того, он находит результат хэширования принятого сообщения M с помощью такой же хэш-функции h(·):

m = h(M).

то получатель признает пару (M,S) подлинной. Доказано, что только обладатель секретного ключа D может сформировать цифровую подпись S по документу M, а определить секретное число D по открытому числу E не легче, чем разложить модуль N на множители.

Рис.6.4. Обобщенная схема цифровой подписи RSA

Если соблюдается равенство вычисленных значений, т.е.

S^E (mod N) = h(M),

Кроме того, можно строго математически доказать, что результат проверки цифровой подписи S будет положительным только в том случае, если при вычислении S был использован секретный ключ D, соответствующий открытому ключу E. Поэтому открытый ключ E иногда называют "идентификатором" подписавшего.

Недостатки алгоритма цифровой подписи RSA.

1. При вычислении модуля N, ключей E и D для системы цифровой подписи RSA необходимо проверять большое количество дополнительных условий, что сделать практически трудно. Невыполнение любого из этих условий делает возможным фальсификацию цифровой подписи со стороны того, кто обнаружит такое невыполнение. При подписании важных документов нельзя допускать такую возможность даже теоретически.

2. Для обеспечения криптостойкости цифровой подписи RSA по отношению к попыткам фальсификации на уровне, например, национального стандарта США на шифрование информации (алгоритм DES), т.е. 10¹⁸, необходимо использовать при вычислениях N, D и E целые числа не менее 2⁵¹² (или около 10¹⁵⁴) каждое, что требует больших вычислительных затрат, превышающих на 20…30% вычислительные затраты других алгоритмов циф-ровой подписи при сохранении того же уровня криптостойкости.

3. Цифровая подпись RSA уязвима к так называемой мультипликативной атаке. Иначе говоря, алгоритм цифровой подписи RSA позволяет злоумышленнику без знания секретного ключа D сформировать подписи под теми документами, у которых результат хэширования можно вычислить как произведение результатов хэширования уже подписанных документов.

Пример. Допустим, что злоумышленник может сконструировать три сообщения M₁, M₂ и M₃, у которых хэш-значения

m₁ = h(M₁), m₂ = h(M₂), m₃ = h(M₃),

причем m₃ = m₁ * m₂ (mod N).

Допустим также, что для двух сообщений M₁ и M₂ получены законные подписи

S₁ = m₁^D (mod N) и S₂ = m₂^D (mod N).

Тогда злоумышленник может легко вычислить подпись S₃ для документа M₃, даже не зная секретного ключа D:

S₃ = S₁ * S₂ (mod N).

Действительно,

S₁ * S₂ (mod N) = m₁^D * m₂^D (mod N) = (m₁m₂)^D (mod N) = m₃^D (mod N) = S₃.

Более надежный и удобный для реализации на персональных компьютерах алгоритм цифровой подписи был разработан в 1984 г. американцем арабского происхождения Тахером Эль Гамалем. В 1991 г. НИСТ США обосновал перед комиссией Конгресса США выбор алгоритма цифровой подписи Эль Гамаля в качестве основы для национального стандарта.

Алгоритм цифровой подписи Эль Гамаля (EGSA)

Название EGSA происходит от слов El Gamal Signature Algorithm (алгоритм цифровой подписи Эль Гамаля). Идея EGSA основана на том, что для обоснования практической невозможности фальсификации цифровой подписи может быть использована более сложная вычислительная задача, чем разложение на множители большого целого числа,– задача дискретного логарифмирования. Кроме того, Эль Гамалю удалось избежать явной слабости алгоритма цифровой подписи RSA, связанной с возможностью подделки цифровой подписи под некоторыми сообщениями без определения секретного ключа.

Рассмотрим подробнее алгоритм цифровой подписи Эль Гамаля. Для того чтобы генерировать пару ключей (открытый ключ – секретный ключ), сначала выбирают некоторое большое простое целое число P и большое целое число G, причем G < P. Отправитель и получатель подписанного документа используют при вычислениях одинаковые большие целые числа P (~10³⁰⁸ или ~2¹⁰²⁴) и G (~10¹⁵⁴ или ~2⁵¹²), которые не являются секретными.

Отправитель выбирает случайное целое число X, 1< X £ (P –1), и вычисляет

Y = G^X mod P.

Число Y является открытым ключом, используемым для проверки подписи отправителя. Число Y открыто передается всем потенциальным получателям документов.

Число X является секретным ключом отправителя для подписывания документов и должно храниться в секрете.

Для того чтобы подписать сообщение M, сначала отправитель хэширует его с помощью хэш-функции h(·) в целое число m:

m = h(M), 1< m < (P –1),

и генерирует случайное целое число K, 1< K< (P –1), такое, что K и (P –1) являются взаимно простыми. Затем отправитель вычисляет целое число a:

a = G^K mod P

и, применяя расширенный алгоритм Евклида, вычисляет с помощью секретного ключа X целое число b из уравнения

m = X* a + K * b (mod (P –1)).

Пара чисел (a,b) образует цифровую подпись S:

S = (a,b),

проставляемую под документом M.

Тройка чисел (M,a,b) передается получателю, в то время как пара чисел (X,K) держится в секрете.

После приема подписанного сообщения (M,a,b) получатель должен проверить, соответствует ли подпись S = (a,b) сообщению M. Для этого получатель сначала вычисляет по принятому сообщению M число

m = h(M),

т.е. хэширует принятое сообщение M.

Затем получатель вычисляет значение

A = Y^a a^b (mod P)

и признает сообщение M подлинным, если, и только если

A = G^m (mod P).

Иначе говоря, получатель проверяет справедливость соотношения

Y^a a^b (mod P) = G^m (mod P).

Можно строго математически доказать, что последнее равенство будет выполняться тогда, и только тогда, когда подпись S=(a,b) под документом M получена с помощью именно того секретного ключа X, из которого был получен открытый ключ Y. Таким образом, можно надежно удостовериться, что отправителем сообщения M был обладатель именно данного секретного ключа X, не раскрывая при этом сам ключ, и что отправитель подписал именно этот конкретный документ M.

Следует отметить, что выполнение каждой подписи по методу Эль Гамаля требует нового значения K, причем это значение должно выбираться случайным образом. Если нарушитель раскроет когда-либо значение K, повторно используемое отправителем, то он сможет раскрыть секретный ключ X отправителя.

Пример. Выберем: числа P =11, G = 2 и секретный ключ X = 8. Вычисляем значение открытого ключа:

Y = G^X mod P = Y = 2⁸ mod 11 = 3.

Предположим, что исходное сообщение M характеризуется хэш-значени-

ем m = 5.

Для того чтобы вычислить цифровую подпись для сообщения M, имеющего хэш-значение m = 5, сначала выберем случайное целое число K = 9. Убедимся, что числа K и (P – 1) являются взаимно простыми. Действительно,

НОД (9, 10) = 1.

Далее вычисляем элементы a и b подписи:

a = G^K mod P = 2⁹ mod 11 = 6,

элемент b определяем, используя расширенный алгоритм Евклида:

m = X * a + K * b (mod (P – 1)).

При m = 5, a = 6, X = 8, K = 9, P = 11 получаем

5 = (6 * 8 + 9 * b)(mod 10)

или

9 * b º – 43 (mod 10).

Решение: b = 3. Цифровая подпись представляет собой пару: а = 6, b = 3.

Далее отправитель передает подписанное сообщение. Приняв подписанное сообщение и открытый ключ Y = 3, получатель вычисляет хэш-значение для сообщения M: m = 5, а затем вычисляет два числа:

1) Y^aa^b (mod P) = 3⁶ * 6³ (mod 11) =10 (mod 11);

2) G^m (mod P) = 2⁵ (mod 11) =10 (mod 11).

Так как эти два целых числа равны, принятое получателем сообщение признается подлинным.

Следует отметить, что схема Эль Гамаля является характерным примером подхода, который допускает пересылку сообщения M в открытой форме вместе с присоединенным аутентификатором (a,b). В таких случаях процедура установления подлинности принятого сообщения состоит в проверке соответствия аутентификатора сообщению.

Схема цифровой подписи Эль Гамаля имеет ряд преимуществ по сравнению со схемой цифровой подписи RSA:

1. При заданном уровне стойкости алгоритма цифровой подписи целые числа, участвующие в вычислениях, имеют запись на 25% короче, что уменьшает сложность вычислений почти в два раза и позволяет заметно сократить объем используемой памяти.

2. При выборе модуля P достаточно проверить, что это число является простым и что у числа (P –1) имеется большой простой множитель (т.е. всего два достаточно просто проверяемых условия).

3. Процедура формирования подписи по схеме Эль Гамаля не позволяет вычислять цифровые подписи под новыми сообщениями без знания секретного ключа (как в RSA).

Однако алгоритм цифровой подписи Эль Гамаля имеет и некоторые недостатки по сравнению со схемой подписи RSA. В частности, длина цифровой подписи получается в 1,5 раза больше, что, в свою очередь, увеличивает время ее вычисления.

Алгоритм цифровой подписи DSA

Алгоритм цифровой подписи DSA (Digital Signature Algorithm) предложен в 1991 г. в НИСТ США для использования в стандарте цифровой подписи DSS (Digital Signature Standard). Алгоритм DSA является развитием алгоритмов цифровой подписи Эль Гамаля и К.Шнорра [121].

Отправитель и получатель электронного документа используют при вычислении большие целые числа: G и P – простые числа, L бит каждое (512 £ L £ 1024); q – простое число длиной 160 бит (делитель числа (P –1)). Числа G, P, q являются открытыми и могут быть общими для всех пользователей сети.

Отправитель выбирает случайное целое число X, 1< X< q. Число X является секретным ключом отправителя для формирования электронной цифровой подписи.

Затем отправитель вычисляет значение

Y = G^X mod P.

Число Y является открытым ключом для проверки подписи отправителя. Число Y передается всем получателям документов.

Этот алгоритм также предусматривает использование односторонней функции хэширования h(·). В стандарте DSS определен алгоритм безопасного хэширования SHA (Secure Hash Algorithm).

Для того чтобы подписать документ M, отправитель хэширует его в целое хэш-значение m:

m = h(M), 1< m < q,

затем генерирует случайное целое число K, 1< K< q, и вычисляет число r:

r = (G^K mod P) mod q.

Затем отправитель вычисляет с помощью секретного ключа X целое число s:

s = 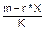mod q.

Пара чисел r и s образует цифровую подпись

S = (r,s)

под документом M.

Таким образом, подписанное сообщение представляет собой тройку чисел [M, r, s].

Получатель подписанного сообщения [M, r, s] проверяет выполнение условий

0 < r < q, 0 < s < q

и отвергает подпись, если хотя бы одно из этих условий не вы-

полнено.

Затем получатель вычисляет значение

w =mod q,

хэш-значение

m = h(M)

и числа

u₁ = (m * w) mod q,

u₂ = (r * w) mod q.

Далее получатель с помощью открытого ключа Y вычисляет значение

v = ((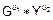) mod P) mod q

и проверяет выполнение условия

v = r.

Если условие v = r выполняется, тогда подпись S = (r,s) под документом M признается получателем подлинной.

Можно строго математически доказать, что последнее равенство будет выполняться тогда, и только тогда, когда подпись S = (r,s) под документом M получена с помощью именно того секретного ключа X, из которого был получен открытый ключ Y. Таким образом, можно надежно удостовериться, что отправитель сообщения владеет именно данным секретным ключом X (не раскрывая при этом значения ключа X) и что отправитель подписал именно данный документ M.

По сравнению с алгоритмом цифровой подписи Эль Гамаля алгоритм DSA имеет следующие основные преимущества:

1. При любом допустимом уровне стойкости, т.е. при любой паре чисел G и P (от 512 до 1024 бит), числа q, X, r, s имеют длину по 160 бит, сокращая длину подписи до 320 бит.

2. Большинство операций с числами K, r, s, X при вычислении подписи производится по модулю числа q длиной 160 бит, что сокращает время вычисления подписи.

3. При проверке подписи большинство операций с числами u₁, u₂, v, w также производится по модулю числа q длиной 160 бит, что сокращает объем памяти и время вычисления.

Недостатком алгоритма DSA является то, что при подписывании и при проверке подписи приходится выполнять сложные операции деления по модулю q:

s = 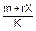(mod q), w = 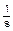(mod q),

что не позволяет получать максимальное быстродействие.

Следует отметить, что реальное исполнение алгоритма DSA может быть ускорено с помощью выполнения предварительных вычислений. Заметим, что значение r не зависит от сообщения M и его хэш-значения m. Можно заранее создать строку случайных значений K и затем для каждого из этих значений вычислить значения r. Можно также заранее вычислить обратные значения K^–1 для каждого из значений K. Затем, при поступлении сообщения M, можно вычислить значение s для данных значений r и K^–1. Эти предварительные вычисления значительно ускоряют работу алгоритма DSA.

Дата добавления: 2013-12-13