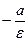Оптичні властивості ліній другого порядку

Дотична до лінії другого порядку.

Поняття директрис. Директоріальна властивість ліній другого порядку.

Поняття ексцентриситету.

Властивості та зображення параболи.

Найпростіші властивості гіперболи та її зображення.

Найпростіші властивості еліпса та його зображення.

План.

Вивчення властивостей еліпса, гіперболи та параболи за канонічними рівняннями.

Лекції 13, 14

1. Як було встановлено вище, канонічне рівняння еліпса 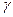записується у вигляді

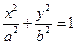, (1)

де 2 а – сума відстаней від довільної точки еліпса до фокусів F ₁ (c;0) та F₂(-c;0), c²=a²-b².

Розглянемо деякі властивості еліпса.

Насамперед, аналізуючи рівняння (1), зробимо висновок, що для його розв’язків виконуються умови 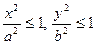, тобто 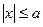,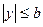. Одержані нерівності означають, що всі точки еліпса розташовані всередині прямокутника із сторонами 2 а та 2 b.

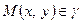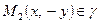Якщо точка , то , і 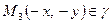. Тому еліпс симетричний відносно координатних осей та початку координат.

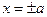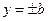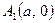При у= 0 із рівняння (1) одержуємо . При х= 0 дістаємо . Отже, еліпс перетинає вісь у точках та 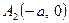, а вісь 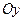─ у точках , 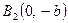. Ці чотири точки називають вершинами еліпса. Відрізки 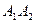та називають відповідно великою та малою осями еліпса. Точку їх перетину О називають центром еліпса. Відрізки ОА ₁= ОА ₂= а та ОВ ₁= ОВ ₂= b називають відповідно великою та малою півосями еліпса.

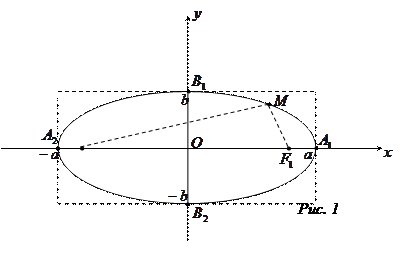Враховуючи симетричність еліпса, дослідимо його форму за допомогою виразу , який визначає рівняння еліпса у першій чверті. Оскільки 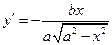, 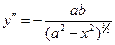та обидва вирази при 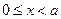від’ємні, то у першій чверті графік еліпса при зростанні 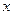від 0 до а спадає від точки 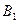до точки , залишаючись опуклим вверх.

Зображення еліпса наведено на рисунку 1.

Розглянемо лінію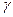, задану параметричними рівняннями

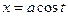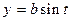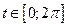, , . (2)

Оскільки

,

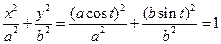то дані рівняння теж задають еліпс. Їх називають параметричними рівняннями еліпса. Покажемо, як за допомогою рівняннь (2) будувати точки еліпса. Побудуємо два кола з центром в точці О, радіуси яких та 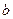(і через точку О проведемо деякий промінь, який утворює з додатнім напрямком осі кут 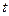(рис. 2). Нехай цей промінь перетинає велике та мале кола в точках 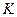,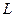відповідно. Через точку 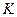проведемо пряму, паралельну до осі 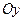, а через точку 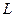- пряму, паралельну до осі . 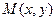Точка їх перетину належить еліпсу, оскільки , .

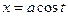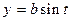2. Розглянемо деякі властивості гіперболи. Канонічне рівняння гіперболи 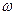було одержано у виді рівняння

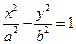, (2)

де 2 а – модуль різниці відстаней від довільної точки гіперболи до фокусів F ₁(c;0) та F ₂(- c;0), c ²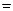 a ²+ b ².

Очевидно, що для розв’язків рівняння (2) виконується умова 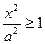. Це означає, що точки гіперболи розташовані в півплощинах, які задаються нерівностями 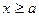та . Аналогічно, як для еліпса, встановлюємо, що гіпербола симетрична відносно початку координат та координатних осей.

Гіпербола перетинає тільки одну із координатних осей, а саме вісь у двох точках: 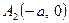та 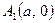. Ці точки називають вершинами гіперболи, а відрізок 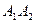–її дійсною віссю. Вісь 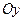гіпербола не перетинає, оскільки рівняння не має розв’язків. Відрізок , де точки 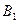та 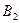розташовані на осі 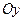на відстані 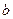від осі , називають уявною віссю. Число називають дійсною, а число 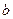- уявною піввіссю гіперболи. Центр симетрії гіперболи (точку 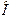) називають центром гіперболи.

Дослідимо форму та побудуємо графік гіперболи. Для цього, враховуючи симетричність лінії, розглядатимемо тільки першу координатну чверть, де, як легко одержати із (2), рівняння гіперболи має вигляд 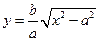. Оскільки 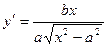, , 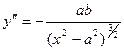то при 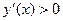, 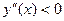. Отже, графік гіперболи зростає при 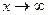, починаючи від точки А ₁ та опуклий вверх.

Розглянемо, як у першій чверті точки гіперболи розташовані відносно прямої . Для цього через довільну точку проведемо вертикальну пряму до перетину з прямою в деякій точці та обчислимо різницю ординат точок N та M (рис. 3). Дістаємо

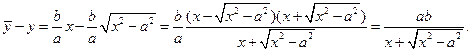
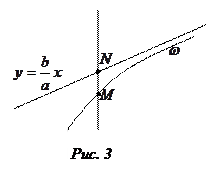Оскільки різниця додатна, то точки прямої розташовані вище від точок гіперболи. При нескінченному зростанні абсциси х точки М дана різниця прямує до 0, тому точки гіперболи необмежено наближаються до прямої.

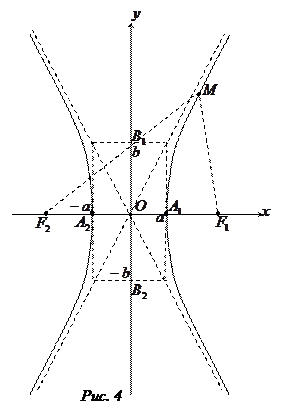Якщо точки деякої лінії необмежено наближаються до певної прямої, рухаючись у 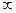, то цю пряму називають асимптотою лінії.

Виконані дослідження дозволяють зобразити гіперболу (рис. 4).

Прямі , які використовувались при зображенні гіперболи, називаються асимптотами гіперболи.

Гіпербола, півосі якої рівні (), називається рівносторонньою. Її канонічне рівняння має вигляд:

.

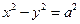У новій системі координат, осі якої співпадають із асимптотами, які у випадку рівносторонньої гіперболи, є перпендикулярними, таку гіперболу можна задати рівнянням 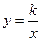, а її графік буде графіком функції оберненої пропорційності.

Більш детально питання про те, як змінюється рівняння лінії при переході до нової системи координат, буде розглянуто в лекції 21.

Параметричні рівняння гіперболи можна задати у вигляді рівностей

, , ,

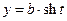де 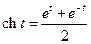(гіперболічний косинус), (гіперболічний синус). Можливі також інші варіанти параметричного задання гіперболи, наприклад,

, , .

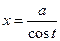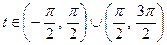Для побудови точок гіперболи можна скористатись наступним прийомом. Будуємо коло довільного радіуса з центром у точці та коло з центром у точці , радіус якого на більший за радіус попереднього кола. Очевидно, що точки перетину побудованих кіл будуть належати гіперболі, оскільки відстані від них до центрів кіл відрізняються на .

3. Розглянемо канонічне рівняння параболи

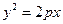. (3)

Нагадаємо, що p –це відстань від фокуса параболи - точки 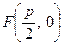до директриси, рівняння якої 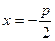. Розглянемо деякі властивості параболи, які випливають із її рівняння.

Оскільки 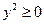, то 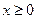, отже, парабола розташована у правій відносно осі 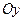півплощині.

Якщо точка 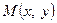належить параболі, то точка теж належить даній лінії, тобто парабола симетрична відносно осі . Дану пряму називають віссю параболи. Існує єдина точка перетину параболи з координатними осями – точка 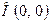. Її називають вершиною параболи.

У першій координатній чверті рівняння параболи задається рівнянням 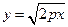. Дана функція монотонно зростає, залишаючись опуклою вверх, оскільки вирази для її похідних при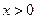

, .

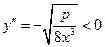Проведені міркування дозволяють побудувати зображення параболи 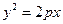(рис. 5).

Параметричні рівняння параболи можна задати у вигляді рівнянь 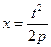, , 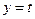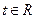. Точки параболи можна будувати наступним чином. Будують коло з центром у точці F радіусом R >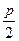та на відстані R від директриси у півплощині, яка містить точку , проводять паралельну до неї пряму. Точки перетину побудованих кола та прямої належать параболі .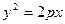

4. Число 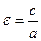називають ексцентриситетом еліпса та гіперболи. Нагадаємо, що число 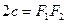дорівнює відстані між фокусами, а – велика піввісь еліпса або дійсна піввісь гіперболи. Для еліпса 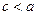, тому його ексцентриситет менший від 1. Для гіперболи 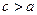, отже, . Ексцентриситет параболи за означенням приймають рівним 1. Підставою для такого означення є так звана директоріальна властивість еліпса та гіперболи, яку ми розглянемо у наступному пункті. Дослідимо, як залежить від зміни ексцентриситету форма лінії.

Для еліпса 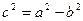, тому 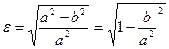. Якщ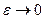о , то 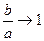, тобто за формою еліпс наближається до кола. Якщо , то 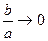, тобто еліпс стискається до осі .

Для гіперболи 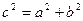, тому 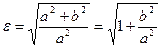. Якщо , то 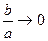, тобто асимптоти утворюють з віссю Ох все менший кут: гіпербола стискається до осі Ох. Якщ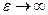о , то 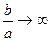. У цьому випадку кут між асимптотами прямує до розгорнутого, а гіпербола стає все більш “витягнутою” вздовж осі .

5. Директрисою параболи 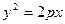ми називали пряму, задану рівнянням 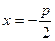. Директрисами еліпса та гіперболи, які задані рівняннями (1) та (2), називають прямі .

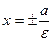Для еліпса 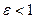, тому 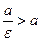, а для гіперболи , тому 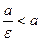, отже, дані прямі не перетинають вказані лінії. Будемо називати директрису d відповідною фокусу F, якщо вони лежать в одній півплощині відносно осі .

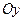Теорема. Відношення відстаней від довільної точки еліпса або гіперболи до фокуса та відповідної директриси є стала величина, яка дорівнює ексцентриситету.

Рис. 7

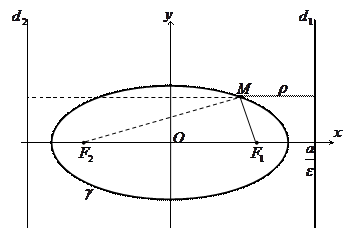Доведення. Доведемо теорему у випадку еліпса (для гіперболи доведення аналогічне). Враховуючи симетричність еліпса, розглянемо випадок правого фокуса F ₁(c;0) та відповідної директриси 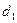, рівняння якої (рис. 7). Нехай 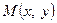– довільна точка еліпса 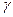. Тоді, враховуючи (8), дістаємо MF ₁=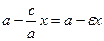. Відстань від точки М до директриси d буде 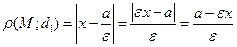. При розкритті модуля враховано, що та 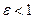, звідки 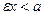. Отже, 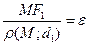. Теорема доведена.

Для параболи (враховуючи означення) відношення відстаней від її довільної точки до фокуса та до директриси рівне 1. Це обґрунтовує той факт, що ексцентриситет параболи приймають рівним 1. Властивість, яка виражається у виді доведеної теореми, називають директоріальною властивістю ліній другого порядку (еліпса, гіперболи, параболи).

6. Нехай на площині задано деяку лінію та — довільна точка на ній. Січна (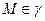) при русі точки 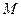по 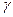буде змінювати своє положення.

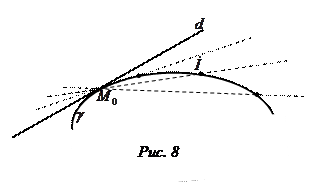
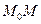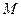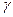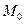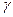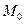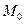Граничне положення січної , коли точка , рухаючись по , необмежено наближається до точки , називають дотичною до лінії у точці (на рис.8 - пряма ), а точку називають точкою дотику

Із курсу математичного аналізу відомо, що якщо лінія 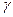задана рівнянням 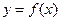, а функція диференційовна в точці , то рівняння дотичної до лінії в точці 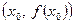запишеться у виді

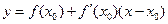. (4)

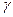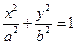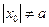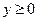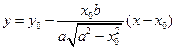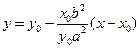Складемо рівняння дотичної до еліпса : у деякій точці (рис. 9). Нехай та . Тоді рівняння еліпса можна задати співвідношенням . Скориставшись рівністю (4), дістаємо рівняння дотичної у виді або . Оскільки , то виконується рівність 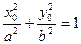. Тому після нескладних перетворень одержане рівняння дотичної можна записати у виді

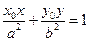. (5)

Аналогічне співвідношення отримуємо у випадку , коли рівняння еліпса запишеться у виді 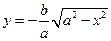. У випадку, коли 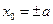(тоді 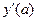не існує і скористатись попередніми міркуваннями не можна) рівняння дотичних запишуться у виді 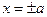, що є частинним випадком співвідношення (5). Доведення останнього твердження можна здійснити аналогічно, записавши рівняння еліпса у виді 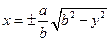. Отже, в усіх випадках рівняння (5) є рівнянням дотичної до еліпса у точці .

Рівняння дотичної до гіперболи 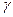: 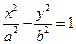у точці запишеться у виді

. (6)

Доведення аналогічне до попереднього.

Розглянемо параболу 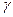, задану рівнянням 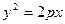, або 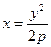та точку . Скориставшись рівнянням дотичної у виді

,

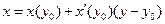дістаємо 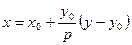, або, оскільки 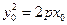, то

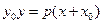. (7)

Співвідношення (7) є рівнянням дотичної до параболи у заданій на ній точці .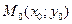

Покажемо простий шлях побудови дотичної до параболи, якщо задане зображення параболи та точка дотику. Нехай дотична до параболи, рівняння якої 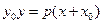, перетинає вісь Оу у точці . Тоді , або 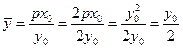. Це означає, що для побудови дотичної досить провести пряму через точку дотику та точку на осі .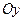

7. До числа найбільш цікавих властивостей еліпса, гіперболи та параболи відносяться їх так звані оптичні властивості. Ці властивості фактично обґрунтовують фізичне походження назви “фокуси”. Сформулюємо та доведемо ці властивості.

Оптична властивість еліпса. Промені світла, які виходять із фокуса дзеркального еліпса та відбиваються від нього, проходять через другий фокус.

Оптична властивість гіперболи. Промені світла, які виходять із фокуса дзеркальної гіперболи та відбиваються від неї, поширюються по променях, які належать прямим, що проходять через другий фокус.

Оптична властивість параболи. Промені світла, які виходять із фокуса дзеркальної параболи та відбиваються від неї, поширюються по променях, які паралельні до осі параболи.

Для доведення цих властивостей достатньо довести, що дотична, проведена у точці 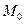, яка належить лінії, утворює однакові кути із фокальними радіусами у випадку еліпса та гіперболи, а у випадку параболи – однакові кути з фокальним радіусом та віссю параболи (рис. 10 та рис. 11).

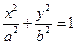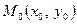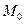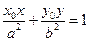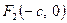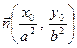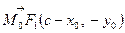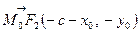Спочатку доведемо оптичну властивість еліпса. Нехай дана лінія задана канонічним рівнянням , а також - деяка точка на еліпсі. Рівняння дотичної, проведеної в точці , як ми знаємо, запишеться у виді . Фокуси еліпса будуть розташовані у точках та . Нехай вектор , який перпендикулярний до дотичної, утворює із векторами та відповідно кути 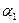та 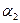. Тоді

.

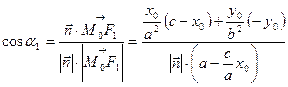
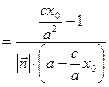
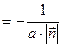Аналогічно,

.

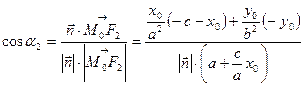
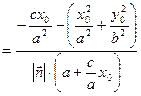
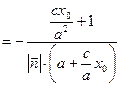
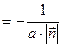Зауважимо, що при виконанні перетворень попередніх виразів було використано відомі нам із попередньої лекції вирази для фокальних радіусів еліпса, а саме 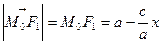, 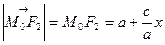. Оскільки . то 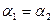, що доводить оптичну властивість еліпса.

Доведення оптичної властивості гіперболи виконується аналогічно.

Розглянемо доведення оптичної властивості параболи. Нехай 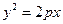– рівняння параболи, точка 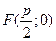– фокус, точка 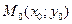– точка на параболі. Тоді рівняння дотичної у точці 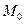запишеться у виді . Для доведення того, що дотична утворює однакові кути із фокальним радіусом та віссю Ох, покажемо, що вектор нормалі дотичної 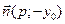утворює однакові кути з вектором 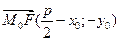та вектором , який паралельний до осі . Нехай 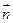утворює кут 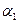з вектором 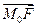та кут з вектором 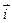. Тоді

,

,

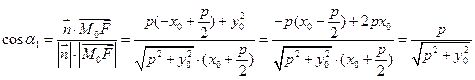отже, , звідки .

Дата добавления: 2013-12-13