Приклади

План.

Рис. 14. Векторне поле.

План.

План

2.1. Виконання найпростіших обчислень над матрицями та векторами.

2.2. Векторні та матричні оператори.

2.3. Векторні та матричні функції.

2.4. Функції, що повертають спеціальні характеристики матриці.

2.5. Додаткові матричні функції.

2.6. Функції сортування векторів та матриць.

2.7. Контрольні запитання.

2.1 Виконання найпростіших обчислень над матрицями та векторами.

Масив - це сукупність даних, що має унікальне ім'я, кінцеве число числових або символьних елементів, упорядкованих заданим чином, які мають певні адреси. У системі MathCAD використаються масиви двох типів: одновимірні (вектори) і двовимірні (матриці).

Індексація елементів масивів. Порядковий номер елемента, який є його адресою, називається індексом. Нижня границя індексації задається значенням системної змінної ORIGIN, що може приймати значення 0 або 1. Для зміни початку індексації можна прямо в документі присвоїти змінній ORIGІN відповідне значення або зробити це, через команду Math головного меню, підменю Options (Опції), використовуючи вкладку Build-In Variables (Вбудовані змінні).

Вектори можуть бути двох типів: вектори - рядки й вектори - стовпці. Незважаючи на те що два цих вектори мають ті самі числові значення елементів, вони різні по типу й дадуть різні результати при векторних і матричних операціях.

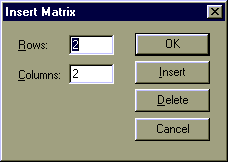
Для введення векторів і матриць можна використати кнопку панелі складальних математичних елементів Matrix, що у свою чергу, включається натисканням відповідної кнопки на панелі Math. Але набагато простіше використати сполучення клавишь [Ctrl+M]. Обидві вище зазначені дії приводять до появи діалогового вікна Insert Matrix, у якому необхідно вказати число рядків і стовпців для введення матриці, або вектора.

У результаті в документі з'являється шаблон матриці, який можна заповнити необхідними даними. Перехід від символу до символу в середині шаблона відбувається за допомогою клавіші Tab (Табуляція). Масив можна визначити й вручну, поелементно. Для задання нижнього індексу використовується клавіша [ (квадратна дужка) або кнопка 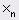, що розміщується на панелі. Якщо індекс подвійний (у матриці), то індекси вводяться через кому. Заповнення масивів може бути організоване за допомогою ранжированих змінних і функцій користувача.

Рис. 4. Приклади виконання дій над матрицями та векторами.

2.2. Векторні та матричні оператори.

Для роботи з векторами та матрицями система MathCAD містить ряд операторів і функцій (див. Таблиця 5). Введемо наступні позначення: для векторів – V, для матриць – M, і для скалярних величин – Z.

Таблиця 5

Оператор	Введення	Призначення оператора;
V1+V2	V1+V2	Додавання двох векторів V1 і V2;
V1-V2	V1-V2	Різниця двох векторів V1 і V2;
-V	-V	Зміна знаку елементів вектора V;
-M	-M	Зміна знаку елементів матриці M;
V-Z	V-Z	Віднімання скаляра Z від вектора V;
Z*V, V*Z	Z*V, V*Z	Множення вектора V на скаляр Z;
Z*M, М*Z	Z*M, М*Z	Множення матриці M на скаляр Z;
V1*V2	V1*V2	Множення двох векторів V1 і V2;
M*V	M*V	Множення матриці M на вектор V;
M1*M2	M1*M2	Множення двох матриць M1 і M2;
V/Z	V/Z	Ділення вектора V на скаляр Z;
M/Z	M/Z	Ділення матриці M на скаляр Z;
M^-1	M^-1	Інверсія матриці M;
M^n	M^n	Піднесення матриці M до степені n;
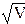
	V\	Обчислення квадратного кореня з V;
| M|	½ M	Обчислення визначника матриці M;
V^T	V Ctrl!	Транспонування вектора V;
M^T	M Ctrl!	Транспонування матриці M;
V	V Ctrl –	Векторизація вектора V;
M	M Ctrl –	Векторизація матриці M;
M^<n>	M Ctrl ^n	Виділення n-го стовпця матриці M;
Vn	V [ n	Виділення n-го елемента вектора V;
Mm,n	M [(m,n)	Виділення елемента (m, n) матриці M.

Під поняттям “векторизація” мається на увазі одночасне проведення математичних операцій у їх скалярному вигляді над усіма елементами вектора або матриці. Це можна розуміти і як можливість паралельних обчислень.

Якщо А и В – вектори, то А*В дає скалярний добуток цих векторів. Але той же добуток під знаком векторизації створює новий вектор, кожен j-й елемент якого є добуток j-х елементів векторів А і В. Векторизація дозволяє виконувати скалярні оператори й функції з масивами.

2.3. Векторні та матричні функції.

Існує також ряд вбудованих векторних і матричних функцій(див. Таблиця6). Приведемо векторні функції, що входять у систему MathCAD:

Таблиця 6

Функція	Призначення функції
lenght(V)	повертає довжину вектора;
last(V)	повертає індекс останнього елемента;
max(V)	повертає максимальний за значенням елемент;
min(V)	повертає мінімальний за значенням елемент;
Re(V)	повертає вектор дійсних частин вектора з комплексними елементами;
Im(V)	повертає вектор уявних частин вектора з комплексними елементами;
ε (i, j, k)	повністю асиметричний тензор розмірності три. i, j, k повинні бути цілими числами від 0 до 2 (або між >ORIGIN й ORIGIN+2, якщо ORIGIN≠0). Результат дорівнює 0, якщо будь-які два аргументи рівні, 1 – якщо три аргументи є парною перестановкою (0, 1, 2), і мінус 1, якщо три аргументи є перестановкою (0, 1, 2), кратної 2 і некратної 4.

Для роботи з матрицями також існує ряд вбудованих функцій (див. Таблиця 7). Вони перераховані нижче:

Таблиця 7

Функція	Призначення функції
Augment(M1, M2)	Поєднує в одну матриці М1 і М2, що мають однакове число рядків;
identity(n)	Створює одиничну квадратну матрицю розміром n*n;
stack(M1, M2)	Поєднує в одну матриці М1 і М2, що мають однакове число стовпців, розташовуючи М1 над М2;
submatrix(A, ir,jr,ic,jc)	повертає підматрицю, що складається із всіх елементів, що знаходяться в рядках від ir по jr і стовпцях з ic по jc (irJjr й icJjc);
diag(V)	Створює діагональну матрицю, елемент головної діагоналі якої – вектор V;
matrix(m,n, f)	Матрицю, у якій (i,j)-й елемент містить значення f (i,j), де i= 0, 1, … m і j= 0, 1, … n;
Re(M)	Повертає матрицю дійсних частин матриці М с комплексними елементами;
Im(M)	Повертає матрицю уявних частин матриці М з комплексними елементами.

2.4. Функції, що повертають спеціальні характеристики матриць.

Спеціальні властивості матриць повертають наступні функції (див. Таблиця 8):

Таблиця 8

Функція	Призначення функції
cols(M)	повертає число стовпців матриці М;
rows(M)	повертає число рядків матриціМ;
rank(M)	повертає ранг матриці М;
tr(M)	повертає слід (суму діагональних елементів) квадратної матриці М;
mean(M)	повертає середнє значення елементів масиву М;
median(M)	повертає медіану елементів масиву М;
cond1(M)	повертає число обумовленості матриці, обчислене в нормі L1;
cond2(M)	повертає число обумовленості матриці, обчислене в нормі L2;
conde(M)	Повертає число обумовленості матриці, обчислене в нормі евклідового простору;
condi(M)	Повертає число обумовленості матриці, основане на рівномірній нормі;
norm1(M)	Повертає L1, норму матриці М;
norm2(M)	Повертає L2, норму матриці М;
norme(M)	Повертає евклідову норму матриці М;
normi(M)	Повертає невизначену норму матриці М.

2.5. Додаткові матричні функції.

У професійні версії MathCAD включений ряд додаткових матричних функцій. Вони перераховані нижче:

Таблиця 9

Функція	Призначення функції
eigenvals(M)	повертає вектор, що містить власні значення матриціМ;
eisenvec(M,Z)	для зазначеної матриці М і заданого власного значення Z повертає належний цьому власному значенню вектор;
eigenvecs(M)	повертає матрицю, стовпцями якої є власні вектори матриці М (порядок розташування власних векторів відповідає порядку розташування власних значень, що повертаються функцією eigenvals);
genvals (M,N)	повертає вектор узагальнених власних значень v, що відповідає рішенню рівняння M · x = vi – N - x (матриці М і N повинні бути дійсними);
genvecs(M,N)	повертає матрицю, стовпці якої містять нормовані узагальнені власні вектори;
+ lu(M)	виконує трикутне розкладання матриціМ: P · M = L · U, L й U - відповідно нижня й верхня трикутні матриці. Всі чотири матриці квадратні, одного порядку;
+ qr(A)	дає розкладання матриці A, A=Q · R, де Q - ортогональна матриця й R — верхня трикутна матриця;
+ svd(A)	дає сингулярне розкладання матриці А розміром n × m: A=U · S ·V^T где U, V– ортогональні матриці розміром m×m і n×n відповідно, S – діагональна матриця, на діагоналі якої розташовані сингулярні числа матриці А;
+ svds(A)	повертає вектор, що містить сингулярні числа матриці А розміром m×n, где m³ n;
Egeninv (A)	повертає матрицю ліву зворотну до матриці А. L·A=E,гдеE –одинична матриця розміром n×n, L– прямокутна матриця розміром n×m, A – прямокутна матриця розміром m×n.

2.6. Функції сортування для векторів і матриць.

Починаючи із третьої версії, у системі MathCAD з'явилися деякі додаткові функції сортування - перестановки елементів векторів і матриць (див. Таблиця 10):

Таблиця 10

Функція	Призначення функції
sort(V)	сортування елементів векторів у порядку зростання їх значень;
reverse(V)	перестановка елементів (після sort) у зворотному порядку;
csort(M,n)	перестановка рядків матриціМ таким чином, щоб відсортованим виявився n-й стовпчик;
rsort(M,n)	перестановка рядків матриціМ таким чином, щоб відсортованим виявився n-й рядок.

2.7. Контрольні запитання.

1 Що називається масивом? Типи масивів. Індексація елементів масивів.

2 Введення векторів і матриць.

3 Назвіть основні оператори системи MathCAD для роботи з векторами і матрицями.

4 Назвіть основні вбудовані функції системи MathCAD для роботи з векторами і матрицями.

5 Назвіть функції, які повертають спеціальні властивості матриць.

6 Перерахуйте додаткові матричні функції, що використовуються у професійні версії MathCAD.

7 Назвіть функції сортування для векторів і матриць.

Лекція 3. Графіка в системі MathCAD.

3.1. Засоби побудови графіків в системі MathCAD.

3.2. Графіки функцій однієї змінної в декартовій системі координат.

3.3. Двовимірні графіки в полярній системі координат.

3.4. Графіки в тривимірному просторі.

3.5. Анімація в MathCAD.

3.6. Контрольні запитання.

3.1. Засоби побудови графіків в системі MathCAD.

MathCAD дозволяє легко будувати двох - і тривимірні гістограми, двомірні графіки в декартових і полярних системах координат, тривимірні графіки поверхонь, лінії рівня поверхонь, зображення векторних полів, просторові криві.

Існує три способи побудови графіків у системі MathCAD:

· можна скористатися командою головного меню Insert (Вставити), вибравши в спадаючому меню команду Graph (Графік) і з списку - тип графіка;

· вибрати тип графіка на панелі Graph (Графік) , що відкривається кнопкою на панелі Math;

· скористатися швидкими клавішами (вони передбачені не для всіх типів графіків).

Розглянемо більш докладно команди меню Insert (Вставити) ->Graph (Графік) (ліворуч зображені відповідні кнопки складальної панелі Math):

X-Y Plot (X-Y залежність) клавіша [@].

Призначена для побудови графіка функції однієї змінної в декартовій системі координат. Будується графік функції y=f(x) у вигляді зв'язаних один з одним пар координат (x_i,y_i) при заданому проміжку зміни для i.

Polar Plot (Полярні координати) клавіші [Ctrl+7].

Призначена для побудови графіка функції r(q), заданої в полярних координатах, де полярний радіус r залежить від полярного кута q.

Surface Plot (Поверхні) клавіші [Ctrl+2].

Призначена для подання функції z=f(x,y) у вигляді поверхні в тривимірному просторі. При цьому повинні бути задані вектори значень x_i й y_j, а також визначена матриця виду A_i,j=f(x_i,y_j). Ім'я матриці A вказується при заповненні рамки-шаблона. За допомогою цієї команди можна будувати параметричні графіки.

Contour Plot (Контурний графік).

Будує діаграму ліній рівня функції виду z=f(x,y), тобто відображає точки, у яких дана функція приймає фіксоване значення z=const.

3D Scatter Plot (3D Точковий).

Служить для точкового подання матриці значень A_i,j або відображення значень функції двох змінних у декартовій системі координат z=f(x,y) у заданих точках. Ця команда може також використовуватися для побудови просторових кривих.

3D Bar Plot (3D Діаграми).

Служить для подання матриці значень A_i,j або відображення значень функції z=f(x,y) у вигляді тривимірної гістограми.

Vector Field Plot (Векторне поле).

Служить для подання двовимірних векторних полів V =(V_x, V_y). При цьому компоненти векторних полів V_x і V_y повинні бути представлені у вигляді матриць. За допомогою цієї команди можна побудувати поле градієнта функції f(x,y).

3D Plot Wizard (виклик майстра для швидкої побудови 3-вимірного графіка).

При виборі цієї команди виникає ряд спливаючих вікон, у яких потрібно вибрати параметри побудови тривимірного графіка (задається тип тривимірного графіка, стиль його зображення, гама кольорів). Графік за замовчуванням будується на проміжку від -5 до +5 (по обох змінних).

3.2. Графіки функцій однієї змінної в декартовій системі координат.

Графік функції y=f(x).

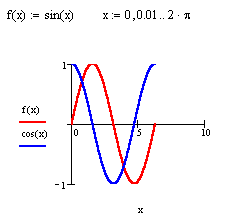
Рис. 5. Графік функції y=f(x).

При виконанні команди Inset -> Graph -> Plot у документі з’являється рамка-шаблон із двома незаповненими осередками для побудови графіка. (Клавіша [@]).

В осередку, що розташовується під віссю абсцис, вказується незалежна змінна x. Її варто визначити заздалегідь як змінну, що приймає значення із проміжку (ранжирувана змінна).

В осередку поруч із віссю ординат необхідно задати функцію f(x), графік якої ми хочемо побудувати. Якщо ця функція була задана заздалегідь, то в осередок досить ввести f(x), у противному випадку варто ввести зображувану функцію в явному вигляді (наприклад, cos(x)).

Після введення x і f(x) у графічній області з'являться ще чотири осередки, які не обов'язково заповнювати. MathCAD автоматично знаходить підходящі значення для x_min, x_max, y_min, y_max. Якщо ж запропоновані MathCAD значення вас не влаштовують, ви можете задати свої.

В MathCAD існує можливість будувати графік функції, не задаючи попередньо проміжок зміни незалежної змінної. За замовчуванням цей проміжок приймається рівним [-10, 10].

Для подання на одній діаграмі графіків декількох функцій необхідно виділити осередок поруч із віссю ординат і через кому ввести другу функцію. За замовчуванням графік цієї функції буде представлений пунктирною лінією іншого кольору.

Криві на площині, задані параметрично.

Рівняння x=f(t), y=y(t), де f(t) і y(t) неперервні при t з (a, b), які встановлюють залежність декартових координат (x,y) точок площини від значення параметра t, визначають на площині криву, задану в параметричній формі.

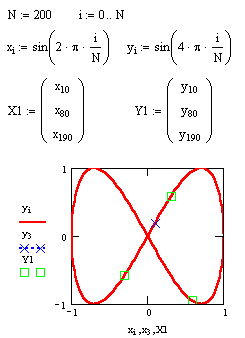
Рис. 6. Криві на площині, задані параметрично.

3.3. Двовимірні графіки в полярній системі координат.

Побудова полярних графіків.

Для побудови полярного графіка необхідно виконати команду Inset -> Graph -> Polar Plot. При цьому в документ з’явиться графічна область із двома незаповненими осередками для побудови графіка. (Клавіші [Ctrl +7]).

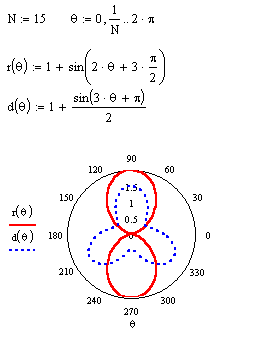
Рис. 7. Побудова полярних графіків

У нижній осередок вводиться полярний кут q. Його варто визначити заздалегідь як змінну, що приймає значення із проміжку (ранжирована змінна). У лівий осередок вводиться полярний радіус r(q) або Re(r(q)) і Im(r(q)). Функція r(q) або задається заздалегідь, або її визначення вводиться безпосередньо в осередок.

Графік у полярних координатах можна побудувати й за допомогою команди X-Y Plot. Тільки в цьому випадку необхідно додатково задати наступні функції: x(q)=r(q)cos(q) і y(q)=r(q)sin(q), а в осередках для абсцис й ординат вказати відповідно x(q) і y(q).

Якщо для деяких кутів q функція не визначена (не існує радіуса з дійсним значенням, він приймає чисто уявнє значення), то MathCAD відображає на графіку тільки дійсні значення радіуса. Але за допомогою функцій Re й Im можна представити на одній круговій діаграмі графіки як дійсної, так і уявної частини функції r(q).

3.4. Графіки в тривимірному просторі.

Побудова графіка функції z=f(x,y) у вигляді поверхні в декартовій системі координат.

Для побудови графіка поверхні можна скористатися двома способами:

1. Якщо вам потрібно тільки подивитися загальний вигляд поверхні, то MathCAD надає можливість швидкої побудови подібних графіків. Для цього досить задати функцію f(x,y) і виконати команду Insert -> Graph -> Surface Plot або натиснути відповідну кнопку складальної панелі Graph (комбінацією клавіш [Ctrl+7]). У графічній області, що з'явилася, під осями на місці шаблона для введення потрібно вказати ім'я (без аргументів) функції. MathCAD автоматично побудує графік поверхні. Незалежні змінні x і y приймають значення із проміжку [-5,5].

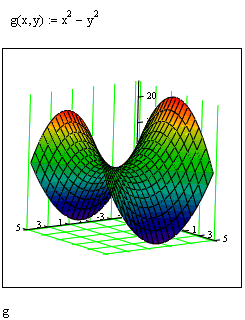
Рис. 8. Побудова графіка функції g=f(x,y).

При необхідності цей проміжок може бути зменшений або збільшений. Для цього необхідно виділити графік і скористатися командою Format -> Graph -> 3D Plot або клацнути правою кнопкою миші за графіком і у контекстному меню вибрати команду Format. У вікні, що з'явилося, 3-D Plot Format на вкладці QuickPlot Data можна встановити інші параметри зміни незалежних змінних x таy.

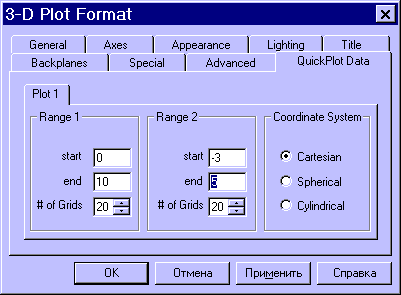
Для побудови графіка поверхні в певній області зміни незалежних змінних або з конкретним кроком їхньої зміни необхідно спочатку задати вузлові точки x_i та y_j, в яких будуть визначатися значення функції. Після (а можна й до) цього потрібно визначити функцію f(x,y), графік якої хочете побудувати. Після цього необхідно сформувати матрицю значень функції у вигляді: A_i,j=f(x_i,y_j).

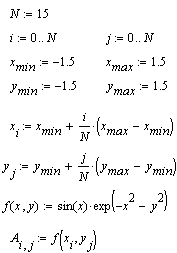
Тепер після виконання команди Insert -> Graph -> Surface Plot у графічній області, що з'явилася, досить ввести ім'я матриці (без індексів).

Якщо ви хочете, щоб вузлові точки були розташовані через рівні проміжки, скористайтеся формулами, зображеними вище.

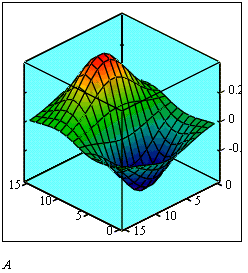
Рис. 9. Побудови графіка поверхні в певній області.

Для побудови графіка ліній рівня даної функції необхідно виконати такі ж дії, які було описано вище, тільки замість команди Surface Plot (Поверхні) варто вибрати команду Contour Plot (Контурний). Аналогічно, за допомогою команди 3D Bar Plot (3D Діаграми) можна побудувати тривимірний стовпчастий графік даної функції, за допомогою команди 3D Scatter Plot (3D Точковий) - тривимірний точковий графік, а за допомогою команди 3D Patch Plot (3D Кусочний) - тривимірний графік поверхні у вигляді незв'язаних квадратних площадок - площин рівня для кожної точки даних, паралельні площини X-Y.

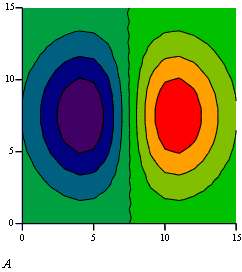
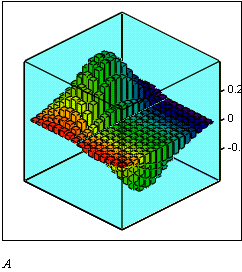
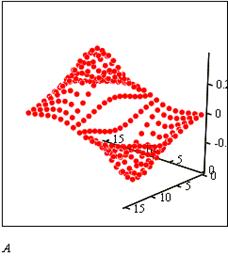
Рис. 11. Побудова графіків: ліній рівня, 3D діаграми та 3D точкового.

Побудова графіка поверхні, заданої параметрично.

Якщо поверхня задана параметрично, це означає, що всі три координати - x, y, z - задані як функції від двох параметрів u та v. Спочатку необхідно задати вектори значень параметрів u_i та v_j. Потім необхідно визначити матриці значень функцій координат x(u,v), y(u,v) і y(u,v).

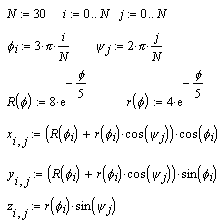
Після вибору команди Surface Plot в MathCAD документі з'явиться графічна область. У вільному осередку внизу області потрібно вказати в дужках імена (без аргументів й індексів) трьох матриць - x,y,z.

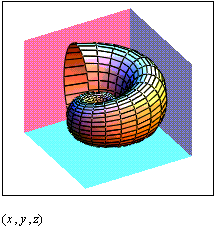
Рис. 12. Побудова графіка поверхні, заданої параметрично.

Крива в просторі.

Тривимірні точкові графіки можна використати для побудови зображення просторових кривих. Просторові криві задаються, як правило, у вигляді (x(t),y(t),z(t)), де t являє собою неперервний дійсний параметр.

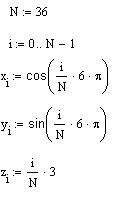
Оскільки при побудові тривимірної точкової діаграми MathCAD дозволяє відображати на графіку тільки окремі точки та з'єднуючі їх лінії, необхідно спочатку визначити три вектори координат - x_i, y_i, z_i.

Просторова крива створюється командою Insert -> Graph ->Scatter Plot (3D Точковий). Можна використати складальну панель Graph, вибравши відповідну піктограму. Для з'єднання точок необхідно на вкладці Appearance вікна форматування графіків вказати опцію Line.

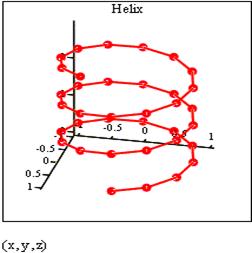
Рис. 13. Крива в просторі.

Векторні та градієнтні поля.

Команда Insert -> Graph -> Vector Field Plot (Векторне поле) служить для подання двовимірних векторних полів v=(vx, vy).

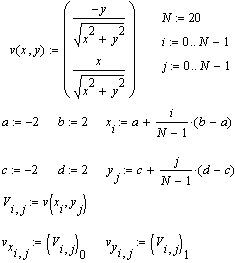
При цьому векторне поле необхідно початку визначити як функцію-вектор-функцію двох координат - x та y. Потім задаються вектори значень вузлових точок x та y. За допомогою цих векторів компоненти векторного поля vx(x,y) і vy(x,y) генеруються у вигляді матриць значень vx_{i, j} і vy_{i, j}.

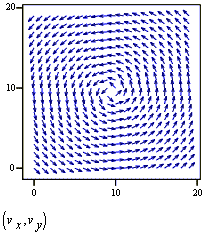
Подібним чином можна побудувати градієнтне поле скалярної функції f(x,y). Градієнтне поле для функції двох змінних являє собою двовимірне векторне поле. Як і в інших випадках, зовнішній вигляд зображення векторного поля можна легко змінити, виконавши подвійне натискання миші в області графіка й змінивши необхідні опції в діалоговому вікні, що відкрилося, 3-D Plot Format.

Рис. 15. Графік поверхні та її градієнтне поле.

Поверхні, отримані обертанням кривих навколо осей.

Цікаві об'ємні фігури можна одержати, обертаючи деяку криву навколо тієї або іншої осі. Побудова цих фігур обертання те саме що параметрично задані поверхні.

При цьому необхідно забезпечити перерахунок координат точок фігури по відомим з геометрії формулам. В MathCAD вбудована функція CreateMesh, за допомогою якої можна побудувати параметрично задані поверхні.

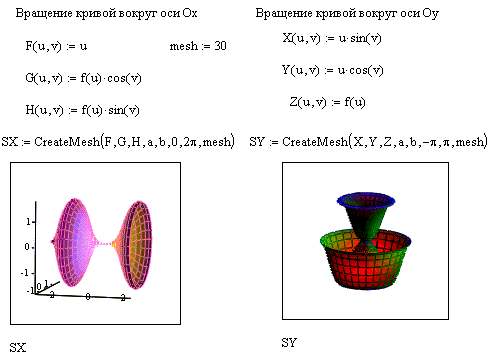
Рис. 16. Поверхні, отримані обертанням кривих навколо осей.

3.5. Анімація в MathCAD.

Починаючи з 6-ї версії, в MathCAD з'явилася можливість створювати анімації. Для її створення будуємо графік функції командою X-Y Plot з підменю Graph меню Insert. Для анімації задається проміжок зміни цілочислового параметра FRAME (за замовчуванням від 0 до 9).

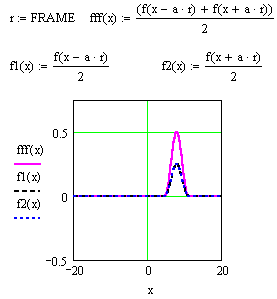
Цей параметр повинен входити у визначення функції, графік якої ви бажаєте прослідити при зміні якогось параметра (насправді ви можете визначити свій параметр довільним чином, аби тільки в ньому був присутній лічильник кадрів Frame) Тепер для створення анімації необхідно виконати наступні дії: 1. Вибрати команду Animate (Анімація) з меню View (Вигляд). При цьому з'явиться діалогове вікно Animate (Анімація). 2. Вкласти побудований графік у маркований прямокутник.

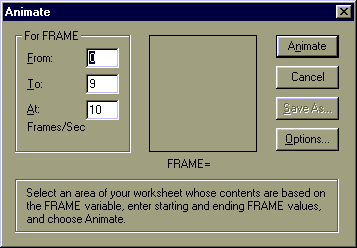
3. Задати мінімальне й максимальне значення параметра FRAME (поля From й To). 4. Задати в поле At кількість відтворених кадрів у секунду. 5. Виконати натискання на кнопці Animate. При цьому в діалоговому вікні ви побачите анімаційні кадри.

6. Щоб відтворити анімацію клацніть на кнопці Play у вікні, що з'явився, Playback(Програвач). 7. Щоб внести зміни в анімацію натиснути на кнопці відкриття меню у вікні Playback. 8. За допомогою команди Save As можна зберегти анімацію у файлі з розширенням AVI.

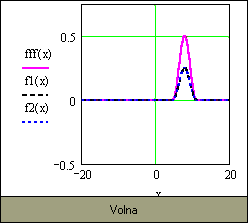
Вбудовування анімації в MathCAD-документ виконується за допомогою Windows Explorer. Для цього необхідно: 1. Запустити Windows Explorer. 2. Натиснути у вікні Windows Explorer на імені AVI-файлу. 3. Перетягнути AVI-файл у відповідний MathCAD-документ. 4. Відтворити анімацію можна за допомогою подвійного натискання в графічній області.

Анімацію можна також відтворити виконавши подвійне натискання на динамічно пов'язаній з відповідним AVI-файлом піктограмі. Для того щоб вмонтувати таку піктограму в MathCAD-документ необхідно:

1. Вибрати команду Object (Об’єкт)з меню Insert (Вставити).

2. Встановити опцію Створити з файлу.

3. Вибрати потрібний AVI-файл за допомогою кнопки Огляд.

4. Встановити опції Зв'язок і У вигляді значка, після чого натиснути на кнопці OK.

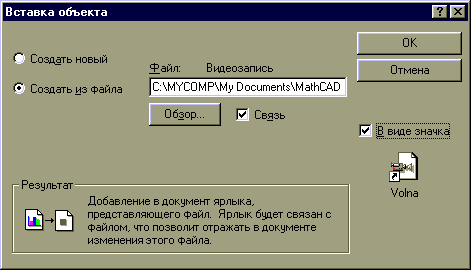
При створенні анімаційних картинок потрібно відключити всі опції автоматичного масштабування графіків і перейти до ручного задання масштабу. Автоматична зміна масштабу може привести до стрибкоподібної зміни розмірів графіка, хоча на практиці він повинен мінятися без стрибків, з дискретністю, обумовленою тільки зміною FRAME=1,2,3... тощо.

3.6. Контрольні запитання.

1. Перерахуйте три способи побудови графіків у системі MathCAD.

2. Охарактеризуйте команди меню Insert (Вставити) > Graph (Графік).

3. Як побудувати графік функції однієї змінної y=f(x) в декартовій системі координат?

4. На якому проміжку будується графік функції y=f(x) за замовчуванням?

5. Як побудувати на одній діаграмі графіки декількох функцій?

6. Як побудувати на площині криву, задану в параметричній формі?

7. Як можна подивитися на загальний вигляд поверхні?

8. Як побудувати графік поверхні в певній області зміни незалежних змінних?

9. Як побудувати графік ліній рівня даної функції?

10. Як побудувати графік поверхні, заданої параметрично?

11. Побудова зображення просторових кривих.

12. Побудова зображення векторних та градієнтних полів.

13. Побудова поверхні, отриманої обертанням кривих навколо осей.

14. Як створити анімаційний об’єкт?

Лекція 4. Символьні обчислення в системі MathCAD.

4.1. Можливості символьного процесора MathCAD.

4.2. Команди меню Symbolics (Символьні операції).

4.3. Палітра символьних перетворень SmartMath.

4.5 Оптимізація.

4.6 Контрольні запитання.

4.1. Можливості символьного процесора MathCAD.

Системи комп'ютерної алгебри використовують спеціальний процесор для виконання аналітичних (символьних) обчислень. Його основою є ядро, що зберігає всю сукупність формул і формульних перетворень, за допомогою яких виконуються аналітичні обчислення. Чим більше цих формул у ядрі, тим надійніша робота символьного процесора і тим ймовірніше, що поставлене завдання буде виконано, зрозуміло, якщо таке рішення існує в принципі (що буває далеко не завжди).

Ядро символьного процесора системи MathCAD - трохи спрощений варіант ядра відомої системи символьної математики Maple V фірми Waterloo Maple Software, у якої MathSoft (розроблювач MathCAD) придбала ліцензію на його застосування, завдяки чому MathCAD стала (починаючи з версії 3.0) системою символьної математики.

Прямий доступ до більшості операцій ядра (можливий у системі Maple V R5/R6), для користувача MathCAD, на жаль, закритий. Наприклад, бібліотечний модуль Maple V містить близько 100 функцій лінійної алгебри, тоді як у модулі MathCAD було тільки три найважливіші функції із цього розділу. Багато функцій і правила перетворення в ядрі використовуються лише для одержання проміжних перетворень. Проте ця обставина не може вважатися аж занадто великим недоліком системи MathCAD. По-перше, тому, що її призначення інше - насамперед рішення завдань у чисельному вигляді, а по-друге, тому, що система Maple V явно надлишкова (у її ядрі близько 2800 функцій і правил перетворення) і орієнтована на користувачів з досить далекими від середніх потреб в рішенні завдань комп'ютерної алгебри (символьної математики).

Введення в систему MathCAD символьних обчислень надає їй нові можливості, які були відсутні в колишніх версіях системи. Символьні обчислення в MathCAD можуть бути реалізовані трьома способами:

· З використання команд підменю позиції Symbolics (Символіка) головного меню.

· З використанням команд панелі Symbolic (Ключові слова символьних обчислень), що включається кнопкою на математичній панелі інструментів. (Починаючи з версії MathCAD 4.0 для активних символьних обчислень застосовується термін SMARTMATH, що представляє комбінацію слів smart і MathCAD, що в буквальному значенні означає розумний MathCAD).

· З використанням команди Optimization позиції головного меню Math.

4.2. Команди меню Symbolics (Символьні операції).

Операції, що вимагаються від символьного процесора, знаходяться в підменю позиціїSymbolics (Символьні операції)) головного меню. Щоб символьні операції виконувалися, процесору необхідно вказати, над яким виразом ці операції повинні виконуватися, тобто потрібно виділити вираз. Для ряду операцій варто не тільки вказати вираз, над яким вони виконуються, але й виділити змінну, щодо якої виконується та або інша символьна операція.

Сам вираз в такому випадку не виділяється: адже й так ясно, що якщо маркер введення виділяє змінну якого-небудь виразу, то цей вираз вже відзначений наявністю в ньому виділеної змінної.

Слід зазначити деякі особливості при роботі з командами меню Symbolics:

· Для символьних обчислень вираз необхідно вказувати явно. Наприклад, неприпустимо вводити деяку функцію користувача F(x) і намагатися знайти її похідні або інтеграл. Це важливе обмеження, про яке потрібно завжди пам'ятати. Однак воно виконується при виконанні обчислень за допомогою функцій системи SmartMath, що описані далі; головне в тім, що для результату символьних обчислень у цьому випадку використовується оператор →.

· Іноді результат обчислень містить вбудовані в систему спеціальні мат. функції; у цьому випадку результат міститься в буфері обміну. Використовуючи команду Paste (Вставити) або клавішу F4, можна вставити вміст буфера обміну в документ, як текст і проаналізувати отриманий результат.

· До недоліків роботи з командами меню Symbolics варто віднести те, що це ручна робота, однокрокова. При подальшому використанні результатів символьних обчислень необхідно за допомогою операцій Copy (Копіювати) та Past (Вставити) присвоїти цей результат деякій змінній або функції. Крім того, при зміні формули, що піддається символьному перетворенню, результат (навіть при встановленому Автоматичному режимі обчислень) не перераховується.

· Якщо операція нездійсненна - система виводить повідомлення про помилку або просто повторює виділений вираз (без змін).

Операції над виділеним виразом.

До операцій з виділеними виразом відносяться (див. Таблиця 11):

Таблиця 11

Операція	Призначення операції
Evaluate (Обчислити)	перетворити виразу з вибором виду перетворень із підменю
Simplify (Спростити)	спростити виділений вираз з виконанням таких операцій, як скорочення подібних доданків, зведення до загального знаменника, використання основних тригонометричних тотожностей тощо
Expand (Розкласти)	розкласти вираз [наприклад, для (Х+ Y) • (Х- Y) одержуємо X^2-Y^2 ]
Factor (Розкласти на множники)	розкласти число або вираз на множники [наприклад, Х^2- Y ^2 дасть (Х+ Y) • (Х- Y) ]
Collect (Зведення подібних доданків)	зібрати доданки, подібні до виділеного виразу, що може бути окремою змінної або функцією зі своїм аргументом (результатом буде вираз, поліноміальний щодо обраного виразу)
Polynomial Coefficients (Поліноміальні коефіцієнти)	знайти коефіцієнти полінома по заданій змінній

Операція Evaluate (Обчислити) містить підменю з наступними командами:

· Evaluate Symbolically [Shift+F9] (Обчислити в символах) — виконати символьне обчислення виразу;

· Floating Point Evaluation... (Із плаваючою точкою) - виконати арифметичні операції у виразі з результатом у формі числа із плаваючою точкою;

· Complex Evaluation (У комплексному вигляді) — виконати перетворення з поданням результату у комплексному вигляді.

Операції з виділеними змінними.

Наступна група символьних операцій виконується над виразами, що вимагають вказівки змінної, стосовно якої виконується операція. Для цього досить встановити на змінній курсор введення. Саме вираз при цьому не вказується окремо, оскільки вказівка в ньому на змінну є одночасно і вказівкою на сам вираз. Якщо вираз містить інші змінні, то вони розглядаються як константи.

В пункті Variable (Змінна) об’єднані операції над виділеними змінними відносяться (див. Таблиця 12):

Таблиця 12

Solve (Розв’язання рівняння)	знайти значення виділеної змінної, при якій вираз що її містить стає рівним нулю (вирішити рівняння або нерівність щодо виділеної змінної)
Substitute (Заміна змінної)	замінити зазначену змінну вмістом буфера обміну;
Differentiate (Диференціювання)	диференціювати весь вираз, що містить виділену змінну, щодо цієї змінної (інші змінні розглядаються як константи);
Integrate (Інтегрування)	інтегрувати весь вираз, що містить виділену змінну, по цій змінній;
Expand to Series... (Розкласти в ряд)	знайти декілька перших членів розкладу функції в ряд Тейлора по виділеній змінній;
Convert to Partial Fraction (Розкласти на елементарні дроби)	розкласти на елементарні дроби вираз, який розглядається як раціональний дріб відносно виділеної змінної.

4.3. Палітра символьних перетворень SmartMath.

При введенні стрілки → після виразу фактично (за замовчуванням) над ним виконується операція Simplify (Спростити). Але що мається на увазі під цим, зрозуміло далеко не завжди, навіть незважаючи на те, що багато символьних операцій системи є очевидними, наприклад обчислення інтеграла або похідної у символьному виді.

При необхідності виконувану операцію можна змінити за допомогою ряду ключових слів, що розташовані на панелі Symbolic, що викликається кнопкою з панелі інструментів Math.

4.4. Приклади:

Оскільки символьні обчислення в MathCAD можна здійснювати в двох різних варіантах розглянемо їх на прикладах:

Приклад №1. Розкласти вираз на співмножники за допомогою головного меню:

1) Введіть вираз sin(2x);

2) Виділіть його повністю;

3) Виберіть в головному меню пункти Symbolics => Expend (Символьні операції => Розкласти)

4) Результат з’явиться трохи нижче у вигляді ще одного рядка.

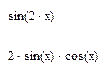
Приклад №2. Розкласти вираз на співмножники за допомогою оператора →:

1) Введіть вираз sin(2x)

2) Натисніть кнопку Expand (Розкласти) на панелі Symbolic (Символика).

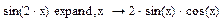
Приклад №3. Скорочення виразів (Simplify):

1-спосіб за допомогою головного меню

1) Введіть вираз;

2) Виділіть вираз повністю, або тільки ту частину яку потрібно скоротити;

3) Виберіть команду Symbolic=> Simplify (Символика=> Спростити).

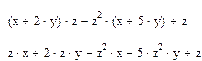
2-спосіб за допомогою панелі Symbolic

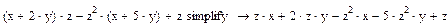
Приклад №4. Скорочення виразів (Simplify) з підстановкою значень змінних:

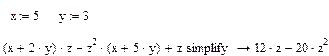
Приклад №5. Розкладання на множники (Factor):

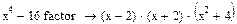
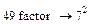
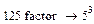
Приклад №6. Зведення подібних множників(Collect):

1) Введіть вираз;

2) Натисніть кнопку Collect на панелі Symbolic;

3) Введіть в містозаповнювач після вставленого ключового слова Collect ім’я змінної, відносно якої потрібно звести подібні множники.

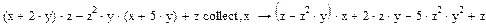
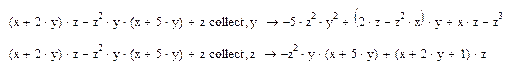
Приклад №7. Знаходження коефіцієнтів полінома (Polynomial Coefficient) (Коефіцієнти полінома):

1) Введіть вираз;

2) Натисніть кнопку Coeffs на панелі Symbolic;

3) Введіть в містозаповнювач після вставленого ключового слова Coeffs аргумент полінома.

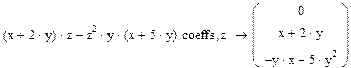
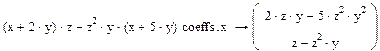
4.5. Оптимізація.

Оптимізація обчислень досягається заміною складної функції або математичного виразу їхнім аналітичним поданням (якщо воно, звичайно, є). Для включення процесу оптимізації необхідно виділити вираз, що потрібно оптимізувати, і виконати команду Optimization позиції головного меню Math.

Ознакою оптимізації виразу є поява після нього червоної зірочки. Крім того, клацнувши правою кнопкою миші й вибравши з контекстного меню команду Show Popup (Показати), можна спостерігати появу вікна з оптимізованим виразом.

Особливий виграш оптимізація може дати при багаторазовому обчисленні складних функцій, що містять інтеграли, похідні, суми, добутки й ряди.

4.6. Контрольні запитання.

1. Призначення та можливості символьного процесора системи MathCAD.

2. Що називається ядром символьного процесора системи MathCAD.

3. Назвіть способи реалізації символьних обчислень в MathCAD.

4. Що означає термін SMARTMATH?

5. Які операції можна виконати над виділеними виразом?

6. Охарактеризувати команди підменю операції Evaluate (Обчислити).

7. Перерахуйте та охарактеризуйте операції з виділеними змінними.

8. Пояснити виконання операцій за допомогою ключових слів, що розташовані на панелі Symbolic.

9. Як оптимізувати обчислення?

10.

Лекція 5. Програмування засобами MathCAD.

Дата добавления: 2013-12-13