Метод Барроу

Метод Херста (метод нормированного размаха)

Метод основан на статистической обработке той физической величины, которая, по мнению исследователя, наиболее полно отражает исследуемое свойство объекта. Этот метод используется для анализа одномерных времен­ных рядов. Пусть имеется ряд наблюдений 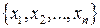некоторой величины 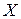. N - объем выборки, - среднее арифметическое ряда наблюдений:

.

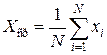Примем за среднеквадратическое отклонение ряда (СКО):

.

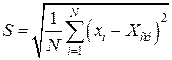Пусть Z- накопленное отклонение ряда Хот среднего (рис. 1.14):

.

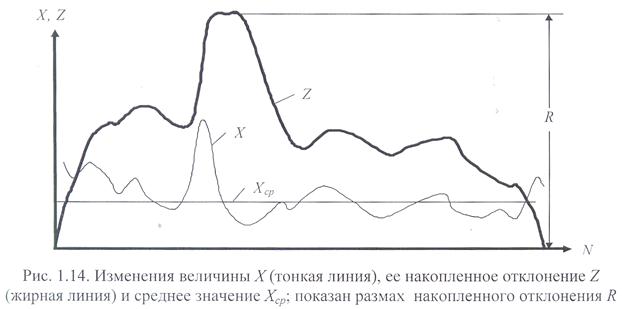
Разность между максимальным и минимальным накопленным отклонени­ем Z назовем размахом накопленного отклонения R (см. рис. 1.14):

.

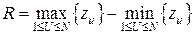На основании этих данных вычисляется параметр Херста R/S - отноше­ние размаха накопленного отклонения R к СКО ряда S - при разных объемах выборки N. Зависимость R/S = f(N) описывается теоретической моделью, вве­денной Мандельбротом, для обобщенного броуновского движения:

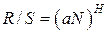, (1.1)

где а - некоторая постоянная для конкретного процесса, 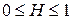- показатель Херста. Фрактальная размерность D определяется как:

. (1.2)

Показатель Херста Н используется также для определения степени долго­временной корреляции (статистической зависимости) между прошлыми при­ращениями и будущими. В теории фракталов эта зависимость определяется вы­ражением

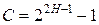. (1.3)

Для нахождения показателя Херста Н зависимость R/S = f(N) строится в двойном логарифмическом масштабе (рис. 1.15), затем полученные экспери­ментальные точки аппроксимируются прямой, угловой коэффициент которой есть Н. Вся область фрактальности ограничена линиями с Н = 0 и Н = 1.

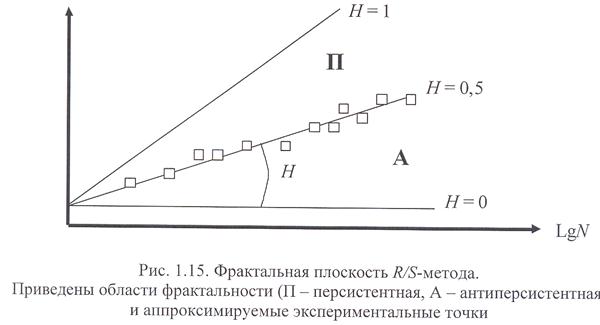
Она делится прямой с Н = 0,5 на персистентную и антиперсистентную (на рис. 1.15 области П и А соответственно). Случай Н = 0,5 соответствует обычному броуновскому движению, в котором отсутствует долговременная корреляция, т.е. С = 0 (см. формулу (1.3)). Персистентность означает, что, если в течение некоторого времени t среднее значение процесса имело тенденцию к возрастанию, то в течение последующего интервала той же длительности t наи­более вероятно сохранение тенденции к возрастанию. И наоборот, если среднее значение процесса в течение некоторого времени t имеет тенденцию к убыва­нию, то наиболее вероятно, что в течение последующего интервала той же дли­тельности t сохранится тенденция к убыванию. Коэффициент долговременной корреляции при Н > 0,5 всегда положителен (см. формулу (1.3)), а при Н < 0,5 - отрицателен. Поэтому при антиперсистентности после возрастания перемен­ной в течение времени t, обычно происходит ее убывание в последующий такой же интервал времени, а при убывании - возрастание.

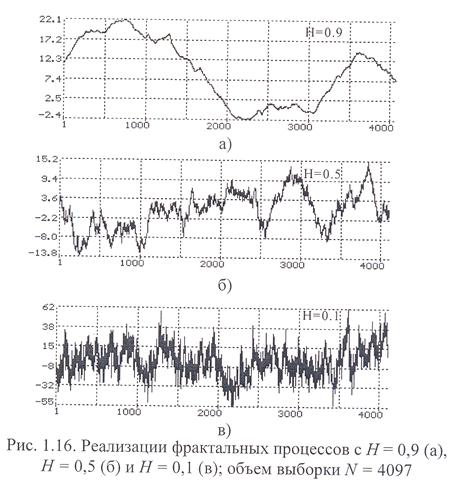
Процессы с Н = 0 имеют наибольшую «зашумленность», которая умень­шается при увеличении значения Н. На рисунке 1.16 продемонстрировано это свойство в отношении трех временных рядов с разными показателями Херста Н = 0,1 (рис. 1.16,а), Н = 0,5 (рис. 1.16,6) и Я = 0,9 (рис. 1.16,в).

Недостатки метода: 1. Зависимость Lg(R/S) = f(Lg(N)) нелинейна, поэтому значения Н для одной выборки могут быть разными, и коэффициент а в выра­жении (1.1) непостоянен и зависит от N. Таким образом, модель (1.1) не всегда справедлива. 2. Неспособность метода различать стационарные случайные про­цессы в зависимости от вида закона распределения плотности вероятности.

Примеры использования метода Херста для различных естественных процессов приведены на рис. 1.17.

По оси абсцисс указана длительность анализируемого периода в годах. Приведены данные для следующих объектов: 1 - сток рек (H = 0,72); 2 - река Рода (H = 0,77); 3 - уровень осадков (H = 0,70); 4 - кольца деревьев (H = 0,80); 5 - слоистые отложения озера Саки (H= 0,76).

Метод основан на статистической обработке той физической величины, которая наиболее полно отражает исследуемое свойство объекта. Этот метод используется для анализа одномерных временных рядов. Пусть имеется ряд на­блюдений 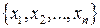некоторой величины 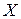объема выборки N. Находится средняя дисперсия приращений W как функция задержки :

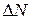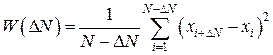. (1.4)

Рис. 1.18. Фрактальная плоскость метода Барроу. Приведены области фрактальности (П - персистентная, А - антиперсистентная, С - стационарная) и аппроксимируемые экспериментальные точки

Зависимость 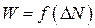описывается теоретической моделью:

, (1.5)

где а - некоторая постоянная для конкретного процесса, - показатель Барроу, который равен показателю Херста 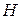, т. е. 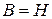. Таким образом фрак­тальная размерность D определяется как:

. (1.6)

Для нахождения показателя Барроу В зависимость 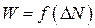строится в двойном логарифмическом масштабе (рис. 1.18), затем полученные экспери­ментальные точки аппроксимируются прямой, угловой коэффициент которой есть В. Вся область фрактальности ограничена линиями с В = 0 и В = 1. Она де­лится прямой с В = 0,5 на персистентную и антиперсистентную (на рис. 1.18 области П и А соответственно). Случай В = 0,5, соответствует обычному бро­уновскому движению, в котором отсутствует долговременная корреляция (на рис. 1.18 область - С).

Недостатки этого метода: 1. Неоднозначность при аппроксимации экспе­риментальных точек прямой на фрактальной плоскости из-за их нелинейного расположения, что не позволяет достаточно точно и правильно описать зависи­мость 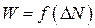. 2. Неспособность метода различать стационарные случайные процессы в зависимости от вида закона распределения плотности вероятности. 3. Высокая вариабельность результатов наблюдения, в результате чего прихо­дится увеличивать количество анализируемых результатов для приемлемых оценок случайной погрешности.

Дата добавления: 2013-12-13