При наложении нескольких стационарных, ординарных, независимых случайных потоков образуется поток, который по своим характеристикам оказывается близким к простейшему

Простейший поток событий

Поток, обладающий свойствами стационарности, ординарности и отсутствием последействия, называется простейшим.

Простейший поток событий используется в качестве модели реального потока заявок в подавляющем большинстве работ по теории массового обслуживания. Это является следствием трех обстоятельств [10]:

1) Использование простейшего потока позволяет получать простые соотношения для оценки эффективности систем массового обслуживания. Для других моделей потоков это удается редко.

2) Простейший поток – это, как правило, тяжелые условия функционирования системы массового обслуживания, так что получаемые таким образом оценки эффективности систем оказываются достаточно надежными.

3) И, наконец, простейший поток в теории массового обслуживания играет такую же роль, что и нормальный закон в теории вероятностей.

Это утверждение верно практически при выполнении единственного условия: среди суммируемых потоков не должно быть потока с интенсивностью сравнимой с суммой интенсивностей остальных потоков. Имеются также некоторые ограничения на последействие внутри каждого потока, которые для прикладных задач обычно несущественны. Практически сложение уже четырех-пяти стационарных, ординарных независимых потоков, сравнимых по интенсивности, достаточно, чтобы свойства суммарного потока оказались близкими к свойствам простейшего потока.

Независимость потоков означает, что число событий, наступающих на двух произвольных интервалах времени t₁ (для одного потока) и t₂ (для другого потока), - независимые случайные величины.

Реальные потоки событий часто являются результатом наложения многих независимых потоков событий и вследствие этого имеют свойства, близкие к свойствам простейшего потока. При наложении n потоков интенсивность суммарного потока определяется как сумма .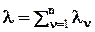

Дата добавления: 2013-12-13