Формула Литтла

Пример

Предельные вероятности состояний

При выполнении определенных условий при t®¥ в системе наступает стационарный режим. При этом вероятности состояний перестают зависеть от времени, то есть становятся постоянными величинами. Эти вероятности называются предельными (финальными, стационарными) [3]. В отличие от вероятностей p_k(t) эти вероятности будем обозначать p_k (без переменной t в скобках т.е. p_k=lim_t→∞p_k(t)).

Если число состояний системы конечно и из каждого состояния можно перейти (за конечное число шагов) в каждое другое, то предельные вероятности существуют и не зависят от начальных условий. Случайный процесс, протекающий в такой системе, называют эргодическим [11].

Для вычисления предельных вероятностей в уравнениях Колмогорова нужно положить все левые части (производные) равными нулю, так как в стационарном режиме вероятности состояний - постоянные величины. Тогда система дифференциальных уравнений превращается в систему линейных, однородных алгебраических уравнений. Совместно с нормировочным уравнением Sp_i=1 эти уравнения позволяют вычислить предельные вероятности. Во многих прикладных задачах интерес представляют именно предельные вероятности.

Уравнения Колмогорова тесно связаны с известными уравнениями Кирхгофа. Для установившегося режима уравнения Колмогорова по аналогии с уравнениями Кирхгофа можно сформулировать так: суммарная интенсивность потоков событий, проходящих через любое возможное состояние системы, равна нулю [14].

Среднее время между отказами некоторого устройства равно t₀ часов. Отказу соответствует переходу S₀ÞS₁ на графе состояний (рис. 3.4). После отказа проводится предварительный осмотр устройства, на который требуется в среднем t₁ часов. В результате предварительного осмотра может быть принято одно из трех решений:

- Требуется замена отказавшего элемента, на что тратится в среднем t₂ часов. Вероятность этого решения q₁₂, ему соответствует переход S₁ÞS₂.

- Требуется замена ряда узлов с последующей регулировкой, на что тратится в среднем t₃ часов. Вероятность этого решения q₁₃, ему соответствует переход S₁ÞS₃.

- Требуется сложный ремонт, регулировка и проведение цикла испытаний, на что тратится в среднем t₄ часов. Вероятность этого решения q₁₄, ему соответствует переход S₁ÞS₄.

Сумма q₁₂+ q₁₃+ q₁₄=1. Плотность распределения времени проведения операции t_i (i=0...4) - экспоненциальная.

Требуется определить среднее время пребывания системы в работоспособном состоянии (S₀).

Решение. Определим интенсивности переходов:

- Из состояния S₀ возможен переход только в состояние S₁, следовательно, l₀₁=l₀=1/t₀.

- Интенсивность перехода из состояния S₁ l₁=1/t₁, а относительные вероятности переходов - q₁₂, q₁₃, q₁₄. Следовательно,

.

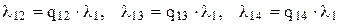- Из состояний S₂, S₃, S₄ возможны переходы только в состояние S₀, следовательно, l₂₀=1/t₂, l₃₀=1/t₃, l₄₀=1/t₄.

Система алгебраических уравнений для определения предельных вероятностей:

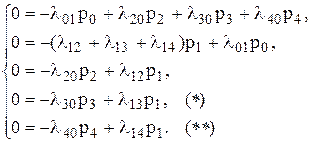
Нормировочное уравнение .

Для нахождения предельных вероятностей все вероятности, начиная с первой, последовательно выражаются через p₀, после чего, воспользовавшись нормировочным уравнением, находится p₀. Из второго уравнения сразу определяется p₁=h₁×p₀. Подстановкой p₁ в уравнения (*) и (**) находятся p_i=h_ip₀ для i =2, 3, 4. Коэффициенты h_i зависят от интенсивностей переходов. Из равенства 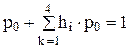находим .

Среднее время пребывание заявки в системе определяется теоремой Литтла:

Для любой системы массового обслуживания, при любом характере потока заявок, при любом распределении времени обслуживания и при любой дисциплине обслуживания среднее время пребывания заявки в системе (T_сист) в стационарном режиме равно среднему числу заявок в системе (K_сист), деленному на интенсивность потока заявок [4 ].

Отметим, что время пребывания в системе заявки, получившей отказ в обслуживании, оказывается равным нулю.

Доказательство. Пусть на вход системы массового обслуживания поступает поток заявок с интенсивностью l. Полагаем, что система функционирует в стационарном режиме достаточно длительное время T (T>>1/l).

За время T на вход системы поступает n»lT заявок, каждая из которых находится в системе время t_i (i=1..n). В число n входят и заявки, получившие отказ в обслуживании. Время их пребывания в системе полагается равным нулю.

Суммарное время пребывания всех заявок в системе

.

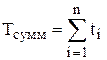Очевидно, что среднее число заявок в системе в течение времени T

K_сист=T_сумм/T.

Если числитель и знаменатель правой части равенства умножить на l, то

.

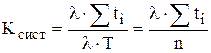Но отношение St_i/n есть ни что иное, как среднее время нахождения одной заявки в системе:

.

Откуда следует так называемая формула Литтла

T_сист=K_сист/l.

При конечном числе каналов (n) и мест для ожидания (m) число заявок, которые могут находиться в системе, ограничено величиной

n+m. Поэтому с увеличением интенсивности входящего потока среднее время пребывания заявки в системе сначала растет (по мере заполнения каналов обслуживания и мест в очереди заявками), а затем вследствие возрастания вероятности отказа в обслуживании начинает уменьшаться так, что асимптотически при l®¥

T_сист ~ (n+m) /l.

Аналогичное равенство в большинстве случаев верно и для среднего времени ожидания заявки в очереди

T_ож=K_ож/l,

где K_ож - среднее число заявок в очереди [4]. Отметим, что для некоторых систем это соотношение может оказаться неверным (в частности, для некоторых систем с инверсным, начиная с конца очереди, обслуживанием заявок [5]).

Дата добавления: 2013-12-13