Распределение Эрланга, первая формула Эрланга

Описание системы. Число каналов обслуживания - n. Поток заявок - простейший с параметром (интенсивностью) l. Параметр потока не зависит от числа заявок, связанных с системой (пуассоновский поток первого рода). Производительность каждого канала обслуживания - m, время обслуживания - T_m=1/m. Заявка, пришедшая в момент, когда все каналы заняты, теряется.

Множество возможных состояний системы:

S₀ - все каналы обслуживания свободны, S_k - занято k каналов (1£k<n), S_n- заняты все n каналов.

При наличии нескольких свободных каналов, канал для обслуживания очередной заявки выбирается случайно. Какие именно k из n каналов заняты, безразлично.

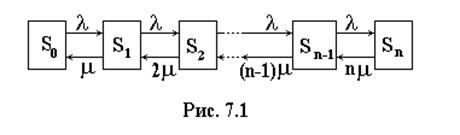
Размеченный граф состояний изображен на рис. 7.1. Поток заявок не зависит от состояния системы (пуассоновский поток первого рода), а интенсивность обслуженных заявок растет пропорционально числу занятых обслуживанием заявок каналов от m до nm.

Пользуясь правилом составления уравнений Колмогорова, можно составить систему дифференциальных уравнений.

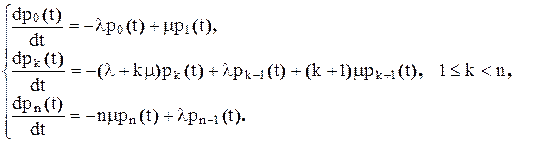
Эти уравнения называются уравнениями Эрланга.

Для решения большинства практических задач достаточно найти предельные вероятности состояний. Для этого в системе дифференциальных уравнений следует приравнять нулю производные вероятностей состояний по времени:

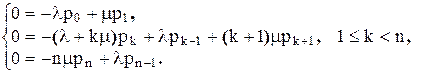
Система однородных алгебраических уравнений совместно с уравнением Sp_i=1 определяет стационарные вероятности состояний.

Граф состояний системы соответствует схеме гибели и размножения, следовательно:

.

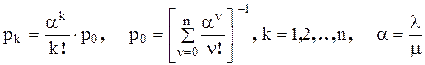Формулы определяют вероятности занятости ровно k каналов из n и называются распределением Эрланга [14] или формулами Эрланга.

Вероятность занятости всех каналов n-канальной системе массового обслуживания

.

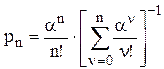Это так называемая первая формула Эрланга. Формула получена для простейшего входящего потока в предположении, что распределение времени обслуживания каждого канала экспоненциальное. Распределение Эрланга справедливо и для произвольного непрерывного закона распределения времени обслуживания при постоянном значении его математического ожидания.

Замечание. Формально, из первой формулы Эрланга следует, что при числе каналов равном нулю (n=0) вероятность занятости всех каналов такой виртуальной системы равна единице при любых α.

Дата добавления: 2013-12-13