Функция является дробью, числитель и/или знаменатель которой содержат иррациональные выражения

Для раскрытия неопределенности этого типа следует освободиться от иррациональностей в числителе и в знаменателе.

Задача 1.3. Найти предел функции:

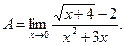(1.4)

Решение. Подставим в данную дробь 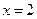, получим:

.

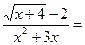
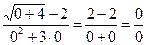Имеем неопределенность типа .

Для освобождения от иррациональности числителя умножим числитель и знаменатель дроби (1.4) на выражение, сопряженное разности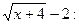

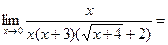
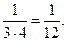
Задача 1.4. Найти предел функции:

(1.5)

Решение. Подставим в числитель и знаменатель дроби величину :

Неопределенность типа . Для ее раскрытия умножим числитель и знаменатель функции (1.5) на произведение сомножителей, сопряженных числителю: 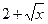и знаменателю: . Получим:

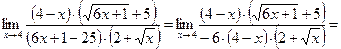
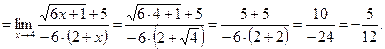
2. Бесконечно большие функции.
Неопределенность типа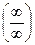

Определение 2.1. Функция 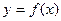называется бесконечно большой (ББФ) при стремлении к , если она по модулю может стать больше любого, сколь угодно большого числа при достаточно малом значении модуля разности . Этот факт обозначается символом.

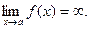(2.1)

Если в определении (2.1) стремится к бесконечности, то равенства (2.1) примет вид:

(2.1^*)

Примеры.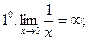

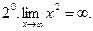
Замечание. Мы не делаем различия в данном контексте бесконечно большие функции с различными знакам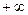и, или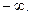

Справедливо утверждение: Функция, обратная бесконечно большой функции, является бесконечно малой. И наоборот, функция, обратная бесконечно малой функции, является бесконечно большой.

Например, 1⁰.

2⁰.

Мы рассмотрим неопределенность типа 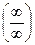в случае отношения многочленов

при .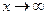

Теорема. Любой многочлен при 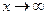неограниченно возрастает, независимо от знаков коэффициентов (мы не различаем или ).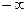

Доказательство. Имеем многочлен n- ойстепени:

(2.2)

вынесем за скобки в самой большой степени:

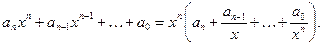(2.2^*)

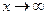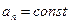При все члены в скобках (2.2^*), кроме первого члена , стремятся к нулю, . Поэтому произведение, а значит и многочлен, неограниченно возрастают.

Раскрытие неопределенности, в свете доказанной теоремы, следует производить следующим образом: в числителе и знаменателе дроби выносим за скобки переменную в самой большой степени для всей дроби, производим сокращение и отбрасываем бесконечно малые функции.

Задача 2.1.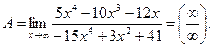

Решение. ,

Замечание. Вычисление пределов этого типа на практике обычно выполняется по-другому: производят деление числителя и знаменателя дроби на переменную в самой большой степени из тех, которые имеются в числителе и знаменателе дроби, и используют свойства пределов.

Решим задачу 2.1 в соответствии с приведенным замечанием.

Задача 2.1^*.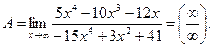

Решение.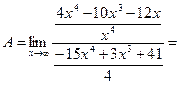

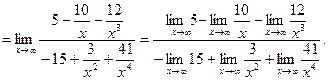
Пределы дробей в числителе и знаменателе равны нулю, поэтому окончательно получаем:

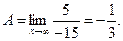
Решение остальных задач мы проведем по образцу решения задачи 2.1^*.

Задача 2.2.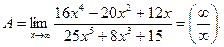

Решение.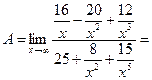

Задача 2.3.

Решение.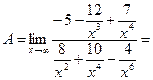

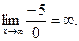
Разобранные примеры позволяют сделать следующие выводы:

· если степени числителя и знаменателя дроби одинаковы, то пределом дроби является число, не равное нулю;

· если степень числителя дроби меньше степени знаменателя, то предел дроби равен нулю;

· если степень числителя дроби больше степени знаменателя, то предел дроби не существует (функция неограниченно возрастает по модулю).

Дата добавления: 2013-12-13