А– приближенное значение величины А.

Запись а» А будем читать "а приближенно равно А". Иногда будем писать А = а, имея в виду, что речь идет о приближенном равенстве.

Если известно, что а < А, то а называют приближенным значением величины А с недостатком. Если а > А, то а называют приближенным значением величины А с избытком.

Разность точного и приближенного значений величины называется погрешностью приближения и обозначается D, т.е.

D = А – а (1)

Погрешность D приближения может быть как числом положительным, так и отрицательным.

Для того чтобы охарактеризовать отличие приближенного значения величины от точного, часто бывает достаточно указать абсолютную величину разности точного и приближенного значений.

Абсолютная величина разности между приближенным а и точным А значениями числа называется абсолютной погрешностью (ошибкой) приближения и обозначается D _а:

D _а = ½ а – А ½ (2)

Пример 1. При измерении отрезка l использовали линейку, цена деления шкалы которой равна 0,5 см. Получили приближенное значение длины отрезка а = 204 см.

Понятно, что при измерении могли ошибиться не более, чем на 0,5 см, т.е. абсолютная погрешность измерения не превышает 0,5 см.

Обычно абсолютная ошибка неизвестна, поскольку неизвестно точное значение числа А. Поэтому в качестве ошибки принимают какую-либо оценку абсолютной ошибки:

D _а <= D _{а пред.} (3)

где D _{а пред .} – предельная ошибка (число, большее нуля), задаваемая с учетом того, с какой достоверностью известно число а.

Предельная абсолютная погрешность называется также границей погрешности. Так, в приведенном примере,
D _{а пред .}= 0,5 см.

Из (3) получаем:

D _а = ½ а – А ½<= D _{а пред.} .

и тогда

а – D _{а пред.} ≤ А ≤ а + D _{а пред.} . (4)

Значит,

а – D _{а пред.} будет приближенным значением А с недостатком,

а

а + D _{а пред} – приближенным значением А с избытком. Пользуются также краткой записью:

А = а ± D _{а пред} (5)

Из определения предельной абсолютной погрешности следует, что чисел D _{а пред} , удовлетворяющих неравенству (3), будет бесконечное множество. На практике стараются выбрать возможно меньшее из чисел D _{а пред}, удовлетворяющих неравенству D _а <= D _{а пред.}

Пример 2. Определим предельную абсолютную погрешность числа а=3,14, взятого в качестве приближенного значения числа π.

Известно, что 3,14<π<3,15. Отсюда следует, что

| а – π |< 0,01.

За предельную абсолютную погрешность можно принять число D _а = 0,01.

Если же учесть, что 3,14<π<3,142, то получим лучшую оценку: D _а = 0,002, тогда π ≈3,14 ±0,002.

4. Относительная погрешность (ошибка). Знания только абсолютной погрешности недостаточно для характеристики качества измерения.

Пусть, например, при взвешивании двух тел получены следующие результаты:

Р₁= 240,3 ±0,1 г.

Р₂= 3,8 ±0,1 г.

Хотя абсолютные погрешности измерения обоих результатов одинаковы, качество измерения в первом случае будет лучшим, чем во втором. Оно характеризуется относительной погрешностью.

Относительной погрешностью (ошибкой) приближения числа А называется отношение абсолютной ошибки D_а приближения к абсолютной величине числа А:

(6)

Так, как точное значение величины обычно неизвестно, то его заменяют приближенным значением и тогда:

(7)

Предельной относительной погрешностью или границей относительной погрешности приближения, называется число d _{а пред.} >0, такое, что:

d _а <= d _{а пред.} (8)

За предельную относительную погрешность можно, очевидно, принять отношение предельной абсолютной погрешности к абсолютной величине приближенного значения:

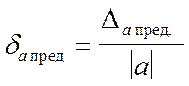(9)

Из (9) легко получается следующее важное соотношение:

∆ _{а пред.}= | a | d _{а пред.} (10)

Предельную относительную погрешность принято выражать в процентах:

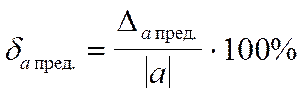
Пример. Основание натуральных логарифмов для расчета принято равным е =2,72. В качестве точного значения взяли е _т = 2,7183. Найти абсолютную и относительную ошибки приближенного числа.

D _е = ½ е – е _т½=0,0017;

.

Величина относительной ошибки остается неизменной при пропорциональном изменении самого приближенного числа и его абсолютной ошибки. Так, у числа 634,7, рассчитанного с абсолютной ошибкой D = 1,3 и у числа 6347 с ошибкой D = 13 относительные ошибки одинаковы: d = 0,2.

О величине относительной ошибки можно примерно судить по количеству верных значащих цифр числа.

Дата добавления: 2013-12-13