Расширенные модели равновесного распределения

ЛЕКЦИЯ 14

К числу наиболее важных расширений и направлений развития модели равновесного распределения относятся:

- модели равновесного распределения для нескольких классов пользователей;

- модели равновесного распределения с переменным спросом на поток;

- стохастические модели равновесного распределения;

- динамические модели равновесного распределения.

Модели многопользовательского равновесия позволяют находить равновесное распределение потоков в системе с несколькими классами пользователей. Напомним, что к разным классам пользователей относятся участники движения, для которых различается обобщенная цена одних и тех же элементов сети (слова «различается цена» относятся также и к ситуации, когда представителям одного из классов пользователей запрещено передвигаться по дуге; в этом случае можно говорить, что цена дуги «равна бесконечности»). Вследствие этого представители различных классов пользователей распределяются по разным путям. Предполагается, что для каждого класса пользователей вычислена отдельная матрица корреспонденций. При этом распределение пользователей разных классов не является независимым друг от друга, поскольку цены дуг и поворотов являются функциями суммарного потока на дуге (повороте). Следовательно, возникает проблема поиска равновесия в системе.

Поскольку транспортные средства, относящиеся к различным классам пользователей, могут давать разный вклад в общую загрузку (например, грузовые автомобили оказывают более существенное влияние на загрузку, чем легковые), суммарные потоки следует измерять в некоторых условных единицах (условных транспортных средствах). В эти же условные единицы должны быть переведены матрицы корреспонденций для всех классов пользователей. Сам вид функций задержки теоретически также может различаться для разных классов пользователей. Однако в модели многопользовательского равновесия действует следующее ограничение: на каждой дуге функции задержки для разных классов пользователей могут отличаться только

на постоянную (не зависящую от суммарного потока) величину. Данное ограничение носит чисто математический характер: именно в таком предположении удается построить интегральный критерий, аналогичный (21), минимум которого достигается на равновесном распределении. Принято следующее «оправдание» такого ограничения: разные классы пользователей имеют разную скорость свободного движения, а затор «действует на всех одинаково».

Пусть M - множество классов пользователей. Обозначим через u^m_a поток по дуге a пользователей класса m є M и предположим, что ценовая функция для каждого класса пользователей имеет вид

(28)

где d^m_a- константы, определяющие разницу в задержке для разных классов при свободном движении. Тогда критерий в задаче многопользовательского равновесия

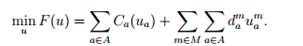(29)

Здесь для краткости опущены слагаемые, относящиеся к задержкам на поворотах. Алгоритм минимизации этого критерия вполне аналогичен описанному выше алгоритму в случае одного класса пользователей.

Модели равновесного распределения с переменным спросом на поток позволяют в рамках единого алгоритма отыскивать как само распределение, так и корреспонденции. Предположим, что объем корреспонденции между каждой парой районов прибытия и отправления задан в виде функции от транспортного расстояния, выраженного в обобщенной цене межрайонного передвижения:

(30)

Здесь c_pq - обобщенная цена передвижения из района q в район p, рассчитанная по кратчайшему пути. Если потоки в сети находятся в равновесном состоянии, то эта цена равна цене всех используемых путей, соединяющих два района. Данная функция называется функцией спроса на передвижения. Функция спроса может содержать параметры, характеризующие емкость районов по прибытию и отправлению, а также параметры, характеризующие наличие альтернативных возможностей передвижений (например, общественный транспорт). Основным требованием к этой функции является монотонное убывание (или, по крайней мере, невозрастание) при увеличении цены межрайонного передвижения.

В задаче поиска равновесного распределения с фиксированным спросом корреспонденции F_pq являются заданными константами. В задаче с переменным спросом они выступают как переменные величины, связанные с потоками по дугам u_pqa соотношениями (18). Задача поиска равновесного распределения с переменным спросом формулируется так: найти такое распределение потоков, при котором для каждой пары районов прибытия и отправления цены всех используемых путем равны между собой и не превосходят цен всех других путей, соединяющих пару районов (т.е. выполнены условия обычного равновесного распределения), и в дополнение корреспонденции F_pq удовлетворяют соотношениям (30). Эта задача также может быть сведена к задаче минимизации глобального критерия следующего вида:

(31)

Данный критерий совпадает с критерием (21) (для краткости опущено слагаемое, относящееся к поворотам), в котором добавлено слагаемое, содержащее интеграл от обратной функции спроса D^-1_pq(f). Эта функция монотонно убывает с ростом корреспонденции, что гарантирует единственность решения.

Данная модель обладает математическим изяществом, однако, на наш взгляд, она не очень хороша для практического применения. В модели объемы корреспонденции представлены однородными величинами, жестко увязанными с единственным вариантом загрузки сети. В реальности загрузка меняется в течение суток (а также в зависимости от времени года), и на формирование корреспонденций влияют, очевидно, усредненные характеристики загрузки. Кроме того, сами корреспонденции существенно неоднородны по составу. Они являются суммами матриц передвижений, совершаемых с различными целями, при этом фактор обобщенных затрат по разному влияет на эти передвижения.

Вместе с тем задача расчета корреспонденций не может быть полностью отделена от задачи распределения корреспонденций по сети. Действительно, существующие модели расчета корреспонденций среди прочих факторов учитывают межрайонные транспортные расстояния. Эти расстояния выражаются через обобщенные цены передвижений, которые, в свою очередь, зависят от загрузки. Для того, чтобы расчет был корректным, необходимо, чтобы обобщенные цены, используемые при расчете матриц, соответствовали тем ценам, которые получаются в результате распределения этих матриц по сети. Этого можно добиться при помощи итеративного процесса

вычисления матриц и загрузки сети. На каждом шаге итерации для расчета матриц используются цены, полученные в результате расчета загрузки на предыдущем шаге. На первом шаге можно воспользоваться ценами, определяемыми по «пустой» сети. Итерации проводятся до тех пор, пока изменение общих показателей загрузки на шаге итерации не станет достаточно малым. В практических приложениях итеративный процесс стабилизируется (изменение общих показателей — менее одного процента) после 3-5 итераций с применением метода скользящего среднего.

Рассмотренные выше модели равновесия основаны на детерминированном поведении пользователей. Они предполагают, что пользователи имеют точное представление о потоках и задержках на всех дугах, одинаково оценивают пути и принимают точные решения при выборе путей. Однако в реальности поведение пользователей стохастично, т.е. содержит существенный элемент случайности. Для учета этой стохастичности была предложена модель стохастического равновесного распределения. Основная идея модели состоит в том, что в ней различается фактическая и предполагаемая тем или иным пользователем цена пути. Предполагаемую цену можно рассматривать как случайную величину, другими словами, разные пользователи случайным образом предполагают разную цену одной и той же дуги. Условие стохастического равновесия тогда формулируется так: распределение называется равновесным, если ни один из участников движения не предполагает, что может улучшить свою индивидуальную цену поездки, изменив путь следования.

Задача поиска стохастического равновесия может быть сведена к следующей задаче оптимизации:

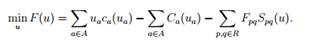(32)

Здесь функции S_pq(u) являются математическими ожиданиями предполагаемых цен передвижения между районами p и q, вычисленных при некотором распределении потоков u. Обозначим через K_pq набор альтернативных путей, соединяющих районы p и q, а через c ^pq_k — фактическую цену пути k є K_pq. Тогда предполагаемую цену можно представить в виде c^^pq_k = c^pq_k + ξ^pq_k, где ξ^pq_k — случайная величина с нулевым математическим ожиданием. Соответственно, математическое ожидание Mc^^pq_k = c^pq_k.

Тогда

(33)

Эта функция зависит от распределения u, поскольку фактические цены, при которых берется математическое ожидание, зависят от u.

Численное решение проблемы (32) значительно сложнее, чем соответствующей нестохастической проблемы. Основная трудность связана с тем, что для вычисления очередного приближения недостаточно знания суммарной загрузки, достигнутой на предыдущих шагах, но требуется явно использовать все межрайонные пути и цены, полученные в ходе итераций. Для решения применяют метод скользящего среднего по доле λ перераспределяемых на каждой итерации потоков.

В последние годы упор в совершенствовании моделей загрузки делается на развитие динамических моделей. Добавление времени как дополнительной переменной чрезвычайно усложняет проблему. Речь идет не просто об увеличении размерности задачи, но и о трудностях в теоретическом определении базовых понятий, например, ценовой функции и самого равновесия. Далее, для того, чтобы отслеживать точное время проезда по той или иной дуге вдоль пути, необходимо более детальное описание условий движения внутри дуги, т.е. применение некоторых имитационных моделей. С учетом итеративного характера поиска равновесия даже при использовании простых имитационных моделей вычислительные ресурсы возрастают чрезвычайно. Подробное обсуждение этого направления выходит за рамки настоящего обзора, отметим только, что существующие на данный момент работы по практическому применению моделей динамического равновесия связаны с использованием суперкомпьютеров и систем с параллельными процессорами.

Дата добавления: 2013-12-13