
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определители третьего и n-го порядка
|
|
|
|
Решение.
1. Временная: "вечную жизнь никогда не требуется страховать".
2. Аксиологическая: " хорошо, что вечную жизнь не требуется страховать".
3. Эпистемическая: " доказано, что вечную жизнь не требуется страховать".
4. Деонтическая: "вечную жизнь обязательно требуется застраховать".
5. Алетическая: "вечную жизнь, возможно, требуется застраховать".
[1] В некоторых случаях можно встретить следующую запись x R y.
§2). Определение 2. Число Δ, записываемое в форме
|
|
 ,
,
где  - действительные числа (k, l =1, 2, 3), называется определителем третьего порядка.
- действительные числа (k, l =1, 2, 3), называется определителем третьего порядка.
В определителе (2) различают 3 строки и 3 столбца. Число  называется элементом определителя; при этом первый индекс k указывает номер строки, а второй индекс l – номер столбца, к которому принадлежит данный элемент. Будем также говорить, что элемент
называется элементом определителя; при этом первый индекс k указывает номер строки, а второй индекс l – номер столбца, к которому принадлежит данный элемент. Будем также говорить, что элемент  находится на пересечении k-й строки и l-го столбца. Элементы
находится на пересечении k-й строки и l-го столбца. Элементы  образуют главную диагональ определителя, а элементы
образуют главную диагональ определителя, а элементы 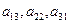 - побочную.
- побочную.
Вычисление определителя третьего порядка с помощью выражения (3) упрощается, если использовать наглядное правило Саррюса:
v с плюсом берутся произведения элементов определителя, стоящих на главной диагонали и в вершинах треугольников с основаниями, параллельными главной диагонали:
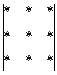 ;
;
v с минусом берутся произведения элементов определителя, стоящих на побочной диагонали и в вершинах треугольников с основаниями, параллельными побочной диагонали:
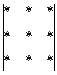 .
.
Например, вычислим определитель:
 .
.
|
 , кроме этого, величина
, кроме этого, величина

называется алгебраическим дополнением элемента  .
.
Теорема 2. 1). Сумма произведений элементов  некоторой строки (столбца) определителя на алгебраические дополнения этих элементов равна величине определителя:
некоторой строки (столбца) определителя на алгебраические дополнения этих элементов равна величине определителя:
|
|
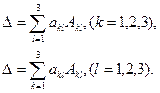
2). Сумма произведений элементов  некоторой строки (столбца) определителя на соответствующие алгебраические дополнения элементов другой строки (столбца) равна нулю:
некоторой строки (столбца) определителя на соответствующие алгебраические дополнения элементов другой строки (столбца) равна нулю:
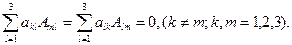
3). Величина определителя не изменится, если к элементам какой-либо его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на число k.
Д-во: 1). Докажем первое свойство для определителя 3-го порядка в случае третьей строки, тогда по формуле (5) имеем:
 Сумму (5) называют разложением определителя по элементам k-й строки, а сумму (6) – разложением определителя по элементам l-го столбца.
Сумму (5) называют разложением определителя по элементам k-й строки, а сумму (6) – разложением определителя по элементам l-го столбца.
Грамотное применение указанных свойств (особенно 3-го) приводит вычисление данного определителя к вычислению определителя более низкого порядка. Например:

|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 428; Нарушение авторских прав?; Мы поможем в написании вашей работы!