Трубопровод с насосной подачей жидкости

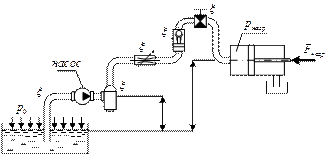
Трубопровод с насосной подачей жидкости может быть разомкнутым (когда жидкость перекачивается из одного источника к потребителю) или замкнутым (когда в системе циркулирует одно и то же количество жидкости).

Рассмотрим, как более простой, случай разомкнутого трубопровода. Такая схема подачи жидкости используется в системах подачи топлива, в простейших системах смазки или системах подачи жидкости в исполнительные органы гидравлических машин (гидроцилиндр). Как правило, обязательными параметрами являются давление и расход жидкости на выходе трубопровода у потребителя.

Запишем уравнение Бернулли для движения жидкости по напорному трубопроводу между сечениями 2-2 и 3-3

,

(21)

где -суммарные потери давления в напорном трубопроводе на участке между сечениями 2-2 и 3-3.

Уравнение Бернулли для движения жидкости по трубопроводу всасывания между сечениями 0-0 и 1-1 имеет вид

,

(22)

здесь 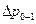-суммарные потери давления во всасывающем трубопроводе на участке между сечениями 0-0 и 1-1.

Из уравнения (22) определим напор жидкости на входе в насос. А для упрощения преобразования расчетных формул пренебрежем составляющей геометрического напора, в связи с ее малой долей в общем балансе энергии потока.

.

(23)

Напор жидкости в сечении 2-2 на выходе из насоса отличается от напора на входе в насос на величину напора сообщаемого насосом жидкости

.

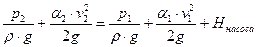(24)

С учетом (23) равенство (24) принимает вид

,

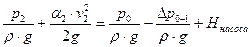(25)

а если учесть, пренебрегая геометрическим напором, равенство (21), то из (25) находим

.

(26)

Если учесть, что , то из (26) легко получить

.

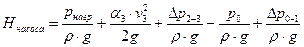(27)

Перегруппировка слагаемых в выражении (27) приводит к результату

.

(28)

Второе слагаемое формулы (27) можно определить через расход жидкости в трубопроводе

.

.

(29)

При условии, что трубопровод имеет постоянный диаметр (, ), коэффициент скоростного напора 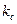равен

,

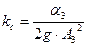(30)

что позволяет переписать (29) в виде

.

(31)

Определяя потери давления на линиях всасывания и нагнетания согласно формулам (3), (4), (8), третье слагаемое (28) перепишется в виде

.

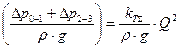(32)

Выражение (32) представляет объединенную напорную характеристику всасывающей и нагнетающей ветвей трубопровода.

Потребный напор насоса, зависящий от величины давления 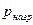, кинетического напора и потерь напора на преодоление местных сопротивлений определяется выражением

.

(33)

и представлен на рис..

Наличие напорной характеристики насоса, как источника энергии для повышения давления рабочей жидкости, позволяет установить рабочую точку согласованной работы всей системы (точка R на рисунке).

Для получения другой рабочей точки необходимо изменить характеристики трубопровода или режим работы насоса за счет увеличения или уменьшения хода плунжеров в аксиально-плунжерном насосе.

Дата добавления: 2013-12-13