В.6. Производные высших порядков

Таблица производных

В. 5. Производные основных элементарных функций

В.4. Производная сложной и обратной функций

Если у есть функция от и: у = f(u), где и в свою очередь есть функция от аргумента х: u = φ(x), т.е. если у зависит от х через промежуточный аргумент и, то у называется сложной функцией от х (функцией от функции): y = f(φ(x)).

Теорема. Производная сложной функции 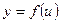, где 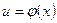, где y и u – дифференцируемые функции своих аргументов, равна произведению ее производной по промежуточному аргументу на производную этого аргумента по независимой переменной:

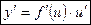или y’_x = y’_u u’_x

.

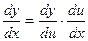Пусть 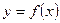–дифференцируемая и строго монотонная функция на промежутке X, 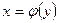– обратная к ней и непрерывная на соответствующем промежутке Y.

Теорема. Для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна обратной величине производной данной функции, т.е.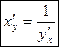

С учётом полученного правила дифференцирования сложной функции таблицу производных можно записать в следующем виде:

№	Функция у	Производная у’
	С
	x
	u^n	n∙u^n^-1∙u’
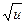
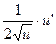
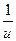
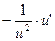
	e^u	e^u∙u’
	a^u	a^u ∙ln a ∙ u’
	ln u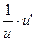
	loga u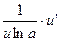
	sin u	cos u∙u’
	cos u	– sin u∙u’
	tg u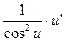
	ctg u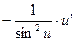
	arcsin u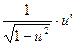
	arcos u	–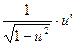
	arctg u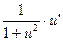
	arcctg u	–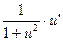

Пример 1. Найти производную функции:

а) у = х + 2; б) y = (2 x – 3)(3 x + 2); в) у = 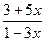; г) у =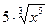; д) у = (x ³ – 2 x ² + 5)⁶; е) 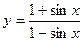; ж) 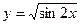; з) y = tg(3 x ² – 1); и) .

Решение. а) у = х + 2

Используя правило дифференцирования (3) и формулы (1), (2), имеем:

у' = (x + 2) ’ = (x) ’ + (2) ’ = 1 + 0 = 1.

б). y = (2 x – 3)(3 x + 2)

y’ = ((2 x – 3)(3 x + 2)) ’ = (2 x – 3) ’ ∙(3 x + 2) + (2 x – 3)∙(3 x + 2) ’ = 2∙(3 x + 2) + (2 x – 3)∙3 = 12 x – 5. Здесь мы использовали правило дифференцирования (5).

в) у =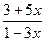

Используя правило дифференцирования (7), имеем

у’ = =.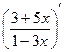

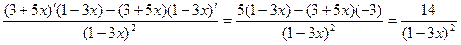г) у =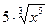

Найдем производную, используя правило дифференцирования (4) и формулу (3).

у' =.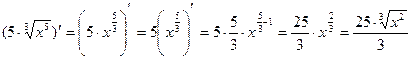

д) у = (x ³ – 2 x ² + 5)⁶

Пусть x ³ – 2 x ² + 5 = и, тогда у = и ⁶. По формуле (3), получим у’ = (и ⁶) ’ = 6 u ⁵∙ u’ = 6(x ³ – 2 x ² + 5)⁵∙(x ³ – 2 x ² + 5) ’ = 6(x ³ – 2 x ² + 5)⁵∙(3 x ² – 4 x).

е)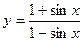

По правилу дифференцирования (7) и формуле (10) получим:

=.

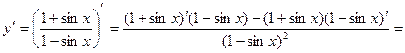
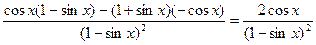ж)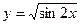

Используя формулы (4) и (10), имеем:

.

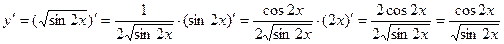з) y = tg(3 x ² – 1).

По формуле (12) имеем:

y' = (tg(3 x ² – 1)) ’ =.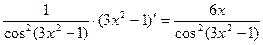

и) .

По формуле (8), а также (3), (4), (5) имеем:

=

=.

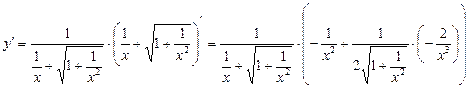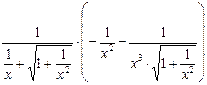Производная называется производной 1-го порядка. Однако производная сама является функцией, которая также может иметь производную.

Производная n -го порядка называется производная от производной (n-1)- го порядка:

.

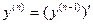Обозначается: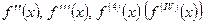и т.д.

Механический смысл 2-й производной: 2-ая производная пути по времени 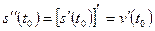равна ускорению точки в момент t₀.

Дата добавления: 2013-12-13