Основная. Геометрические и физические приложения кратных интегралов

СПИСОК ЛИТЕРАТУРЫ

Вопросы для самоконтроля

A b X

Геометрические и физические приложения кратных интегралов.

Тройной интеграл в декартовой системе координат (ДСК).

Отличие тройного интеграла от двойного заключается в том, что при нахождении тройного интеграла интегрирование ведется не по двум, а по трем переменным, а областью интегрирования является не часть плоскости, а некоторая область в трёхмерном пространстве.

Суммирование производится по области v, которая ограничена некоторой поверхностью j(x, y, z) = 0.

Здесь х₁ и х₂ – постоянные величины, у₁=у₁(х) и у₂=у₂(х), z₁=z₁(х,у) и z₂ = z₂(х,у).

1) Вычисление площадей в декартовых координатах.

Y

y = j(x)

S

y = f(x)

Рисунок 2.

Площадь S, показанная на рисунке может быть вычислена с помощью двойного интеграла по формуле:

3) Вычисление объемов тел.

Объём V цилиндроида, ограниченного сверху непрерывной поверхностью z = f(x,y), снизу плоскостью z=0 и с боков прямой цилиндрической поверхностью, вырезывающей на плоскости ХОУ область S, равен:

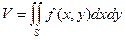
Вычисление массы неоднородного тела.

где плотность w – величина переменная.

Вычисление объемов тел с помощью тройного интеграла.

Если поверхность тела описывается уравнением f(x, y, z) = 0, то объем тела может быть найден по формуле:

Здесь х₁ и х₂ – постоянные величины, у₁=у₁(х) и у₂=у₂(х), z₁=z₁(х,у) и z₂ = z₂(х,у).

1. Что такое кратные интегралы?

2. Как вычисляются кратные интегралы?

3. Как вычисляются площади с помощью двойного интеграла?

4. Как вычисляются объемы тел?

1. Дмитрий Письменный, Конспект лекций по высшей математике. М., АЙРИС ПРЕСС,2007.600с.

2. Данко П.Е., Попов Л.Г., Кожевникова Т.Е., Данко С.И. Высшая математика в упражнениях и задачах. 2006.-187с. ООО Изд. Мир и образование.

Дата добавления: 2013-12-13