Поверхностные интегралы первого рода

Поверхностные интегралы

В разных физических вопросах часто встречаются функции, заданные на той или иной поверхности. Примерами таких функций могут служить плоскость распределения зарядов на поверхности проводника, освещенность поверхности, скорость жидкости, протекающей через некоторую поверхность, и т.д.

Пусть в каждой точке некоторой поверхности σ, ограниченной линией L определена функция ƒ(p). Разобьем поверхность σ произвольными кривыми на части ∆σ_1, ∆σ_2, ..., ∆σ_n. Площадь каждой из них обозначим так же

∆σ _1, ∆δ_2, ..., ∆δ_n. Выбрав в каждой из них произвольную точку Р_i составим сумму

n

∑ ƒ (Р_i) ∆δ_i, которую называют интегральной суммой.

i=1

Предел этой суммы при max ∆σ_i→0 называют поверхностным интегралом первого рода и обозначают 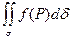или ,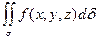

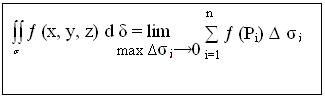при этом переменные x, y, z связаны условием: точка (x, y, z) лежит на поверхности σ.

Его вычисление сводится к вычислению двойного интеграла.

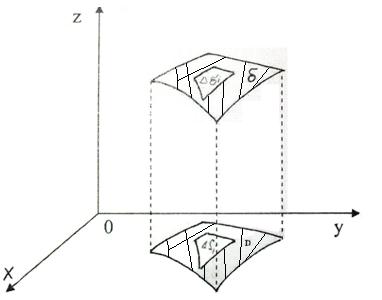
Поверхность σ задана уравнением z = z(x, y) и проектируется на плоскость xoy в области D.

Площадь поверхности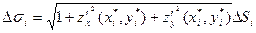

где (x_i^*, y_i^*) – некоторая точка, лежащая в области D (т.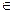∆S_i)

где ∆S_i – площадь площадки ∆S_i.

т. P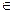_i ∆ σ _i

P_i = P(x_i, y_i, z_i)

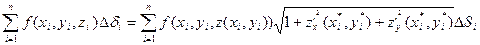
z

0 y

Д

Вычисляя предел левой и правой части при max ∆σ_i→0 (maxΔS_i→0) получим в левой части поверхностный интеграл, а в правой части двойной интеграл по области D.

 

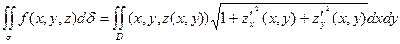
Замечание. Если поверхность σ задана уравнением: x=x(y,z) или y = y(x,z),

то поверхностные интегралы вычисляются аналогично по формулам:

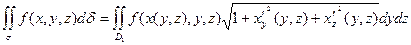
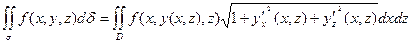
Пример (Б.3876) Вычислитьƒ(z + 2x + 4/3 y) dσ,

где σ – часть плоскости x/2 + y/3 + z/4 = 1, лежащая в первом октанте.

z

4 z = 4(1 – x/2 – y/3)

0 3

2 y

x

область D, т.е. ее проекция на пл. xoy

y

3

x/2 + y/3 = 1

0 2 x

2 3(1-x/2)

∫∫ (z + 2x + 4/3y)dδ = ∫ dx ∫ (4(1 – x/2 – y/3) + 2x + 4/3y) =

σ 0 0

2 3(1-x/2) 2 3(1-x/2) 2 2

∫ dx ∫ 4dy = 4∫ y│ dx = 4*3 ∫ (1-x/2) dx = 12(x – x³/4)│ = 12(2 – 4/4) = 12

0 0 0 0 0 0

Дата добавления: 2013-12-13