Простейшие векторные поля

Оператор Гамильтона и векторные дифференциальные операции второго порядка.

Введенные нами основные понятия векторного анализа: градиент, дивергенция, ротор – удобно представлять с помощью символического вектора («набла-вектор»):

1) Произведение набла-вектора на скалярную функцию u(P) дает градиент этой функции:

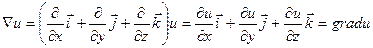
2) Скалярное произведение набла-вектора на векторную функцию дает дивергенцию этой функции:

3) Векторное произведение набла-вектора на векторную функцию дает ротор этой функции:

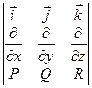
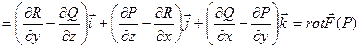
Набла-вектор называют оператором Гамильтона.

Действия взятия градиента, дивергенции и ротора будут векторными дифференциальными операциями первого порядка. В них участвуют только первые производные от скалярных функций.

Перейдем теперь к векторным дифференциальным операциям второго порядка.

Пусть имеется скалярное поле u(P) и мы нашли градиент этого поля grad u. Поле градиента является векторным полем, и мы можем искать его дивергенцию и ротор: div grad u и rot grad u.

Если имеется векторное поле 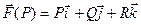, то оно порождает два поля: скалярное поле 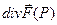и векторное поле 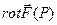. Следовательно мы можем находить градиент первого поля: 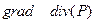и дивергенцию и ротор второго поля: 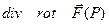и . Всего мы имеем пять векторных дифференциальных операций второго порядка. Особенно важными из них являются три, рассмотрим их.

а)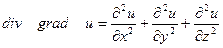

Действительно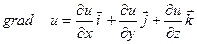

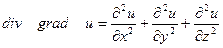
Правая часть называется оператором Лапласа от функции u и обозначается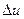

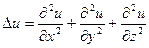
С помощью набла-вектора можно записать так:

б) с помощью набла-вектора можно записать так:

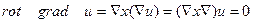
векторное произведение одинаковых векторов = 0

в) 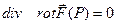с помощью набла-вектора можно записать так:

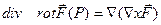
Имеем смешанное произведение трех векторов, из которых два вектора одинаковы. В этом случае такое произведение равно нулю.

Остальные две векторные операции второго порядка: и 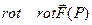- встречаются реже.

Простейшими векторными полями являются такие, для которых либо , либо 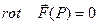, либо равны нулю и дивергенция и ротор.

1) Векторное поле, для всех точек которого дивергенция равна нулю, называется трубчатым или соленоидальным.

Поясним смысл этого названия.

Возьмем в этом поле какую-нибудь площадку S₀ и проведем через каждую точку ее границы векторные линии. Эти линии ограничивают часть пространства, называемую векторной трубкой. Жидкость при своем течении все время движется по такой трубке, не пересекая ее стенок.

2) Если во всех точках поля ротор равен нулю: 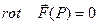, то поле называется безвихревым или потенциальным.

3) Векторное поле, являющееся одновременно и потенциальным и трубчатым, называется гармоническим.

Пример 1. Найти , если

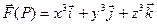
Решение.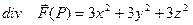

Пример 2. Найти 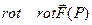, если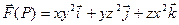

Решение.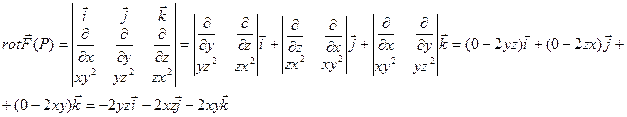

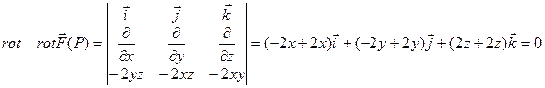
Дата добавления: 2013-12-13