Условный экстремум. Условный экстремум находится, когда переменные х и у, входящие в функцию u = f( x, y), не являются независимыми

Условный экстремум находится, когда переменные х и у, входящие в функцию u = f(x, y), не являются независимыми, т.е. существует некоторое соотношение

j(х, у) = 0, которое называется уравнением связи.

Тогда из переменных х и у только одна будет независимой, т.к. другая может быть выражена через нее из уравнения связи.

Тогда u = f(x, y(x)).

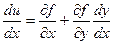
В точках экстремума:

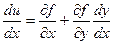=0 (1)

Кроме того:

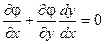(2)

Умножим равенство (2) на число l и сложим с равенством (1).

Для выполнения этого условия во всех точках найдем неопределенный коэффициент l так, чтобы выполнялась система трех уравнений:

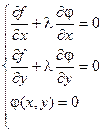
Полученная система уравнений является необходимыми условиями условного экстремума. Однако это условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум.

Выражение u = f(x, y) + lj(x, y) называется функцией Лагранжа.

Пример. Найти экстремум функции f(x, y) = xy, если уравнение связи:

2x + 3y – 5 = 0

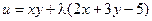
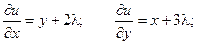
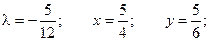
Таким образом, функция имеет экстремум в точке .

Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа.

Выше мы рассмотрели функцию двух переменных, однако, все рассуждения относительно условного экстремума могут быть распространены на функции большего числа переменных.

Дата добавления: 2013-12-13