Упражнения. Лекция 19. Функции, способы их задания

Лекция 19. Функции, способы их задания. Основные функции. Понятие предела функции, бесконечно малые и бесконечно большие функции, непрерывность, классификация точек разрыва.

Упражнения

1. (n = 1, 2, 3,…). Развернуть эту последовательность значений переменной x и найти ее предел.

Ответ: ; .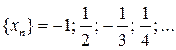

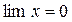2. 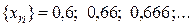. Найти .

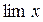Ответ: .

3. 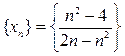(n = 1, 2, 3,…). Найти .

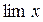Ответ: .

4. Пользуясь определением предела последовательности, доказать, что

а) 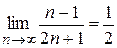; б) ; в) .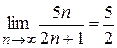

5. Доказать, что последовательность с общим членом - монотонно возрастающая.

6. Доказать, что последовательность с общим членом 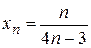- монотонно убывающая.

Пусть даны множества действительных чисел Х и Y. Функциональной зависимостью (функцией) называется закон, по которому каждому значению величины , называемой аргументом, ставится в соответствие некоторое (единственное) число из множества Y. Множество Х называется областью определения функции. (D(f)). Множество значений (E(f)) числовой функции f называется множество всех , для которых существует хотя бы одно такое, что f(x)=a. В математике словом «функция» называют и закон (правило) соответствия f и величину f(x).

Существует три способа задания функцию:

1) Аналитический – задание функции формулой, показывающей способ вычисления значения функции по соответствующему значению аргумента. При аналитическом способе задания функция может быть задана явно, когда дано выражение у через х, т.е. формула имеет вид , неявно, когда x и y связаны между собой уравнением вида F(x,y)=0, а также параметрически, когда соответствующие друг другу значения x и y выражены через третью переменную величину t, называемую параметром.

2) Табличный – указание значений функции от соответствующих значений аргумента. Способ применяется в тех случаях, когда область определения функции состоит из конечного числа значений. В виде таблиц записывают результаты экспериментального исследования каких-либо процессов.

3) Графический. Для функции заданной графиком, по чертежу находятся приближенно значения y, отвечающие данным значениям х.

Вспомним основные функции, изученные в курсе элементарной математике и их графики.

1) линейная , D(f) =R, E(f) =R при и {b} при k =0. Графиком является прямая с угловым коэффициентом k, который равен тангенсу угла наклона прямой к оси абсцисс. Число b – ордината точки пересечения графика с осью ординат.

2) квадратичная , D(f) =R, E(f) = или . Графиком является парабола.

3) обратно-пропорциональной зависимости , D(f) = , E(f) = . Графиком является гипербола.

4) показательная , D(f) =R, E(f) =.

5) логарифмическая , D(f) = , E(f) = R.

6) тригонометрические функции:

y=sinx, D(f) =R, E(f) = .

y=cosx, D(f) =R, E(f) = .

y=tgx, D(f) =, E(f) =R.

y=ctgx, D(f) =, E(f) =R.

7) обратные тригонометрические функции:

y=arcsinx, D(f) = , E(f) = .

y=arccosx, D(f) = , E(f) = .

y=arctgx, D(f) =R, E(f) = .

y=arcctgx, D(f) =R, E(f) = .

Пусть – некоторая функция, рассматриваемая на некотором числовом множестве оси ох (например, на отрезке или на интервале этой оси). И пусть x ₀ – некоторая внутренняя или граничная точка этого множества. Для отрезка такой точкой x ₀ может быть любая точка этого отрезка. А для интервала – любая точка этого интервала, включая не принадлежащие ему его границы a и b.

Будем рассматривать значения функции для аргумента x, последовательно принимающего некоторые значения (x ₁; x ₂; … x_n; …), выбранные таким образом, что . При этом может оказаться, что соответствующая последовательность значений (y ₁; y ₂; … y_n; …) функции стремится к некоторому конечному или бесконечному y ₀ (). И если это стремление y к y ₀ осуществляется при любом способе стремления x к x ₀, то число y ₀ называется пределом функции при . И записывается это так:

(1)

(читается: предел функции при равен y ₀). Обратно, равенство (1) означает, что при функция . Причем стремление y к y ₀ осуществляется при любом способе стремления x к x ₀.

Отметим, что если x ₀ – граничная точка числового множества оси ох, на котором рассматривается функция (крайняя левая или крайняя правая его точка), то x может стремиться к x ₀ либо только справа, либо только слева. Такое стремление x к x ₀ обозначают соответственно (x стремится к x ₀ справа) и (x стремится к x ₀ слева) – рис. 1.

А соответствующие пределы функции называют соответственно пределами справа и слева:

– предел функции при справа; (2)

– предел функции при слева.

Такие пределы функции называются односторонними.

Если x ₀ – внутренняя точка числового множества оси ох, на котором рассматривается функция , то для нее можно искать оба односторонних предела – и предел справа (при ), и предел слева (при ). Кроме того, можно искать и общий (двусторонний) предел (2.1). Очевидно, что если этот двусторонний предел существует и равен y ₀, то существуют и оба односторонних, и оба они равны y ₀. Обратно, если оба односторонних предела (2) существуют и равны, то существует и равен им и двусторонний предел (1).

Суть пределов функции, как двустороннего, так и односторонних, можно наглядно проиллюстрировать. В частности, сделаем это для двустороннего предела (1).

Согласно определению этого предела, при любом способе стремления x к x ₀ соответствующее значение функции стремится к y ₀. То есть если x подойдет достаточно близко к x ₀, то и подойдет достаточно близко к y ₀. Иначе говоря, как бы ни была мала -окрестность точки y ₀, должна найтись такая соответствующая ей -окрестность точки x ₀, что как только x в своем стремлении к x ₀ попадет в -окрестность точки x ₀, соответствующее этому x значение функции попадет в -окрестность точки y ₀ (рис. 2).

Для иллюстрации же односторонних пределов (2.2) в рис. 3.5 нужно заменить двустороннюю -окрестность точки x ₀ на соответствующую одностороннюю или .

Дадим формализованное определение предела функцию Число А называется пределом функции f(x) при х, стремящемся к a (или в точке а), если для любого наперед заданного положительного числа (хотя бы и как угодно малого) можно найти такое положительное число , что для всех значений х, входящих в область определения функции, отличных от а и удовлетворяющих условию , имеет место неравенство .

В определении предела функции вовсе не требуется, чтобы функция f(x) была непременно определена в точке а. Для того чтобы функция f(x) имела возможность стремиться к пределу при , необходимо лишь, чтобы в области её существования были точки, как угодно близкие к а и отличные от а.

Среди функций, имеющих предел в точке, выделяют бесконечно малые и бесконечно большие функции. Функция f(x) называется бесконечно малой при или , еслиили . Функция f(x) называется бесконечно большой при , если имеет место одно из равенств ,,.(Аналогично при )

Для сравнения бесконечно малых функций обычно рассматривают их отношения.

Если отношение имеет конечный и отличный от нуля предел, т.е. если , а следовательно, , то бесконечно малые и называются бесконечно малыми одного порядка.

Если отношение двух бесконечно малых стремится к нулю, т.е. (а ), то бесконечно малая называется бесконечно малой величиной высшего порядка, чем бесконечно малая , а бесконечно малая называются бесконечно малой низшего порядка, чем бесконечно малая .

Теперь перейдем к рассмотрению такого важнейшего понятия, как непрерывность функции.

Если функция определена для всех x из некоторого отрезка или интервала оси ох, и ее график для указанных х – сплошная (непрерывная) линия, то такая функция называется непрерывной на этом отрезке или интервале. Непрерывная на отрезке или интервале функция считается непрерывной в любой конкретной точке x₀ этого отрезка или интервала.

Если функция непрерывна в некоторой точке x ₀, то очевидно, что при значение функции (рис.3.). Причем это стремление y к y ₀ при будет иметь место и при , и . Действительно, стремление x к x ₀ вызывает для непрерывной функции стремление (приближение) точки M к точке М ₀, а значит, и стремление ординаты y точки М к ординате y ₀ точки М ₀, с какой бы стороны от точки М ₀ ни находилась точка М.

Стремление к при означает, что

(3)

Если подытожить все вышесказанное, то мы получим одну из возможных форм определения непрерывности функции.

Функция называется непрерывной в точке x ₀, если функция имеет в точке x ₀ одинаковые односторонние пределы, которые равны частному значению функции в точке x ₀.

От этого определения можно перейти к другой формулировке понятия непрерывности функции: функция называется непрерывной, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. Введем обозначения (см. рис. 3)

– приращение аргумента x в точке x ₀;

– приращение функции в точке x ₀, (4)

то стремление к при , то есть выполнение равенства (3), означает, что при . И обратно, если при и , то это означает, что при аргументе функция , а значит, выполняется равенство (3). Таким образом, условие

при () (5)

и условие (3) равносильны. Оба они, в разной форме, представляют собой математическое определение непрерывности функции в заданной точке x₀.

Если функция непрерывна в каждой точке некоторого промежутка, то говорят, что она непрерывна на этом (открытом) промежутке.

Функция называется непрерывной на закрытом промежутке , если она непрерывна в каждой внутренней точке этого промежутка и, кроме того, имеет предел справа в точке a и предел слева в точке b.

Если условие непрерывности (3) (или равносильное ему (5)) функции в некоторой точке x ₀ не выполняется, то функция называется разрывной в точке x₀. А сама такая точка x ₀ называется точкой разрыва функции . Например, точка x₀ является точкой разрыва функции и на рис. 4(а), и на рис. 4(б), и на рис. 4(в).

Действительно, для рис.4 (а) условие непрерывности (3) не выполняется сразу по двум причинам:

1) – не существует; 2) ; ; , значит, – не существует.

Для рис. 4 (б) условие непрерывности (3) тоже, очевидно, не выполняется. Действительно,

(существует, хоть и не является конечным числом), но – не существует.

На рис. 4 (в) из сплошного (непрерывного) графика функции вырезана точка М ₀ и перемещена по вертикали в другое положение М. В итоге точка x ₀ станет точкой разрыва функции , ибо для неё получаем:

1) – существует; 2) – существует; 3) Однако , то есть . Если вернуть точку М на место (в точку М ₀), то функция опять станет непрерывной в точке x ₀. Поэтому разрыв этой функции в точке x₀, изображенныйна рис. 4 (в), называется устранимым.

Рисунки 4 (а)-(в) наглядно иллюстрируют суть точек разрыва функций. А именно, точкой разрыва данной функции является такое значение x₀ аргумента x этой функции, при котором нарушается сплошность (непрерывность) ее графика.

Точки разрыва имеют свою классификацию. Точканазывается точкой разрыва первого рода, если в этой точке функция имеет конечные, но не равные друг другу правый и левый пределы. Если хотя бы один из односторонних пределов в точке равен или , или не существует, то в данной точке функция терпит разрыв второго рода.

Если пределы справа и слева при не совпадают, то функция в данной точке терпит разрыв, однако, если пределы справа и слева совпадают, то утверждать, что функция непрерывна нельзя. Рассмотрим для примера функцию . Составим две таблицы:

		0,5	0,8

		1,5	1,2

Итак, подходим ли к со стороны меньших значений (как в первой таблице) или со стороны больших значений (как во второй) предел один и тот же:

.

Но так как значение функции при найти нельзя, она в этой точке не определена, поэтому не является непрерывной.

Точка называется точкой устранимого разрыва функции , если при существуют и равны между собой односторонние пределы, но в точке функция либо не определена, либо имеет значение , отличное от значений односторонних пределов в этой точке.

Вспомним, что графики основных элементарных функций (линейной , квадратичной , обратно-пропорциональной зависимости и т.д.) являются сплошными (непрерывными) линиями для всех x, для которых эти функции определены. И разрыв указанные линии терпят лишь при тех значениях , при которых соответствующие им функции не определены. Такие x ₀ и являются точками разрыва элементарных функций.

Например, квадратичная функция определена для любых x. И ее график (парабола) является сплошной (непрерывной) линией при любых x. То есть точек разрыва у функции нет. А вот функция определена для любых x, кроме . И соответственно ее график (гипербола) является сплошной (непрерывной) линией для любых x, кроме , где она терпит разрыв (рис. 5 (а) и 5 (б)).

Указанным выше свойством основных элементарных функций обладают, как можно доказать, и любые конечные комбинации этих функций (их суммы, произведения, функции от функций, то есть сложные функции и т.д.). То есть любые функции , составленные из основных элементарных функций (а с другими функциями, собственно говоря, мы встречаться практически и не будем) будут непрерывны для всех значений аргумента x, для которых они определены. А следовательно, точками их разрыва будут лишь те отдельные изолированные точки x₀, в которых они не определены. Изолированные – это такие точки x ₀, что в любой окрестности [;] этих точек функция определена, и лишь в самих точках x ₀ она не определена.

Например, функция определена, а следовательно, и непрерывна для любых x, кроме точек и . В окрестности каждой из этих точек функция определена, и только в самих этих точках она не определена. Значит, эти точки и и есть точки разрыва данной функции y.

Выясним, заодно, и характер поведения этой функции возле каждой из ее точек разрыва – и справа, и слева.

1) Пусть ; тогда ; .

2) Пусть ; тогда ; .

3) Пусть ; тогда ; .

4) Пусть ; тогда ; .

Отобразив установленное поведение функции y возле ее точек разрыва, получим важные фрагменты графика функции (они изображены на рис. 6 сплошными линиями). Другие же элементы графика функции (обозначенные пунктиром) требуют для своего детального изображения дополнительного исследования. Но об этом поговорим позже, когда будет рассмотрена полная схема исследования функций.

Рассмотрим теперь несколько примеров вычисления пределов функций.

Пример 1. Найти .

Решение. Функция определена, а следовательно, и непрерывна в любой точке , в том числе и в точке . Поэтому, пользуясь равенством (2.3) для непрерывных функций, получаем:

Впрочем, этот результат и так очевиден, ибо, естественно, при функция .

Пример 2. Найти .

Решение. Функция определена, а следовательно, и непрерывна для всех x, кроме . То есть – точка разрыва этой функции. Поэтому найти искомый предел при по формуле (3), которая применяется лишь для непрерывных в точке x ₀ функций, нельзя. Но это в данном случае и не важно – значение предела и так очевидно. Действительно, совершенно очевидно, что при любом способе стремления функция . То есть

.

Пример 3. Найти .

Решение. При функция , очевидно, стремится к нулю. Поэтому .

Пример 4. Найти .

Решение. Как и в примере 2, воспользоваться равенством (3) здесь нельзя, так как – точка разрыва функции . Однако очевидно, что при функция , а при функция . То есть односторонние пределы типа (2) здесь разные:

; .

А значит, общий не существует.

1. Доказать, что .

2. Найти пределы:

1) ; 2) ; 3) ; 4) ;

5) ; 6) ; 7) ; 8)

Ответы: 1) 8; 2) ; 3) 0; 4) 4; 5) 1; 6) 6; 7) 3; 8) 3.

Дата добавления: 2013-12-13