Применение производной функции к нахождению точек экстремума функции

Напомним, что термин «точки экстремума» – это общее название точек максимума и минимума функции. А под ними, в свою очередь, понимаются абсциссы вершин и впадин графика функции (проекции вершин и впадин на ось о х). Или, если не прибегать к геометрической трактовке, точки экстремума функции – это те значения ее аргумента x, при которых функция принимает экстремальные (пиковые) значения – максимальные или минимальные. Точек экстремума у функции столько, сколько вершин и впадин у ее графика.

Определение 1: функция f(x) в точке х₁ имеет максимум, если значение функции f(x) в точке х₁ больше, чем ее значения во всех точках некоторого интервала, содержащего точку х₁. Другими словами, функция f(x) в точке х=х₁ имеет максимум, если при любых 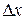(положительных и отрицательных), достаточно малых по абсолютной величине.

Определение 2: функция f(x) в точке х₂ имеет минимум, если значение функции f(x) в точке х₁ меньше, чем ее значения во всех точках некоторого интервала, содержащего точку х₂. Другими словами, функция f(x) в точке х=х₂ имеет минимум, если при любых 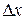(положительных и отрицательных), достаточно малых по абсолютной величине.

Рассмотрим рис.3. На нем изображен график непрерывной функции , имеющей и интервалы возрастания, и интервалы убывания, и точки экстремума:

Интервалы возрастания функции помечены знаком (+), а интервалы убывания – знаком (–). Согласно доказанной выше теореме 1, это заодно и знаки производной функции .

Точками экстремума данной функции являются точки (x ₁, x ₂, x ₃, x ₄). Причем точки x ₁ и x ₃ – точки максимума, а x ₂ и x ₄ – точки минимума. Точки x ₅ и x ₆ точками экстремума функции не являются, так как соответствующие им точки графика М ₅ и М ₆ – не вершины и не впадины этого графика.

Точки экстремума разделяют интервалы возрастания и убывания функции. В точках максимума совершается переход от возрастания функции (слева от точки максимума) к ее убыванию (справа от точки максимума). То есть в точках максимума знак производной функции меняется с (+) слева на (–) справа. А в точках минимума, наоборот, совершается переход от убывания функции к ее возрастанию. То есть в точках минимума знак производной функции меняется с (–) слева на (+) справа.

Сами же точки экстремума не принадлежат ни к интервалам возрастания, ни к интервалам убывания функции. Потому в точках экстремума производная не может быть ни положительной, ни отрицательной. Значит, в этих точках она или равна нулю, или ее не существует вообще.

Этот вывод понятен и с геометрической точки зрения. Действительно, производная функции, согласно ее геометрического смысла, связана с касательной к графику функции. А именно, представляет собой тангенс угла наклона этой касательной к оси ох. Но точкам экстремума функции соответствуют на ее графике вершины и впадины, в которых касательная к графику или параллельна оси ох (если вершина или впадина графика округлая), или эта касательная отсутствует вообще (если вершина или впадина острая). В первом случае угол наклона 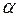касательной к оси ох равен нулю. Значит, и 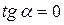, а значит, и производная 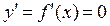. Во втором случае угол 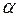не существует вообще, а значит, не существует для данной точки экстремума x и производная 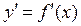. В частности, для рис. 3 имеем:

; – не сущ.; – не сущ.; .

Однако заметим, что не любая точка x, в которой производная равна нулю или не существует, непременно будет точкой экстремума. В частности, на рис. 3 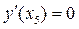; не существует, и тем не менее ни точка x ₅, ни точка x ₆ не являются точками экстремума функции .

Все сказанное выше о точках экстремума функции можно оформить в виде теоремы.

Теорема 4. Необходимое условие экстремума.

Для того, чтобы некоторая точка x являлась точкой экстремума функции , необходимо, чтобы в этой точке производная 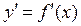этой функции или равнялась нулю, или не существовала. Это условие не является достаточным.

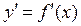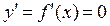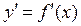Таким образом, лишь те точки (значения x), в которых производная функции равна нулю или не существует, могут быть точками экстремума этой функции. Но еще не факт, что все такие точки будут точками экстремума. Иначе говоря, точки (значения x), в которых или не существует, являются лишь подозрительными на экстремум или критическими точками. Чтобы выяснить суть каждой подозрительной точки, нужно посмотреть знак производной слева и справа от неё. Здесь возможны три варианта:

1) Если слева от подозрительной на экстремум точки знак производной (+), а справа (–), то эта подозрительная точка – точка максимума.

2) Если справа от подозрительной на экстремум точки знак производной (–), а справа (+), то эта подозрительная точка – точка минимума.

3) Если слева и справа от подозрительной на экстремум точки знак производной один и тот же, то эта подозрительная точка – не точка экстремума.

Сказанное наглядно иллюстрирует рис. 3. Таким образом, становится понятной и очевидной следующая

Дата добавления: 2013-12-13