Учет влияния фильтрационных сил

Простейшие методы расчетов устойчивости

4.4.1. Устойчивость откосов в идеально сыпучих грунтах (ϕ ≠0; с=0)

Имеется откос с углом заложения α, при заданном φ для песка, слагающего откос (рис.4.4, а). Рассмотрим равновесие частицы, свободно лежащей на поверхности откоса: т.к. грунт обладает только внутренним трением, то устойчивость будет обеспечена, если T≤T’.

Задавшись весом частицы P и учитывая, что коэффициент внутреннего трения грунтов 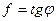, получим;

;

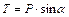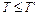, откуда 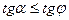или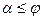

при α=φ в идеально сыпучих грунтах угол естественного откоса – α равен углу внутреннего трения грунта.

Окончательно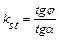

при откос обладает необходимым запасом устойчивости.

В случае, если требуется определить угол заложения будущего откоса с запасом устойчивости, то α соответственно определиться как:

Если уровень подземных вод находится выше подошвы откоса, возникает фильтрационный поток, выходящий на его поверхность, что приводит к снижению устойчивости откоса.

В этом случае при рассмотрении равновесия частицы необходимо добавить гидродинамическую составляющую D.

Гидравлический градиент в точке выхода потока равен:

, а гидравлическая составляющая в единице объема грунта равна:

γ_w – удельный вес воды;

n – пористость.

Учитывая, что вес единицы объема грунта P =γ V, где V =1.

Уравнение предельного состояния запишется как:

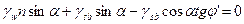
т.к.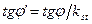, после преобразования получим

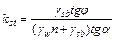
Угол заложения откоса при заданном нормативном коэффициенте устойчивости:

.

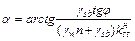4.4.3. Устойчивость вертикального откоса в идеально связных грунтах (ϕ=0; с≠0)

Если высота откоса, сложенного связными грунтами, не превышает предельного значения h₀, то связный грунт может держать вертикальный откос.

Наиболее неблагоприятное напряженное состояние возникает у подошвы откоса в т.А (рис.4.1, в) Именно здесь начинает формироваться состояние предельного равновесия.

Максимальное главное напряжение в этой точке равно природному, т.е. 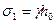. Поскольку откос ограничен свободной вертикальной поверхностью, минимальное главное напряжение в т.А равно нулю, т.е. .

Условие предельного равновесия имеет вид:

Учитывая, что здесь φ=0 (по условию задачи), а также подставляя сюда σ₁ и σ₃, после преобразования будем иметь: .

Коэффициент устойчивости вертикального откоса при h ≤ h ₀:

Высота вертикального откоса в идеально связных грунтах, отвечающего заданному запасу устойчивости:

4.4.4. Устойчивость вертикального откоса в грунтах, обладающих трением и сцеплением (ϕ ≠0; с≠0)

Пр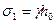и и , используя полное выражение условия предельного равновесия получим:

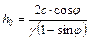
Нетрудно заметить, что учет внутреннего трения грунта приводит к некоторому увеличению предельной высоты вертикального откоса.

4.5. Инженерные методы расчёта устойчивости откосов и склонов

В проектной практике применяются инженерные методы, содержащие различные упрощения.

Дата добавления: 2013-12-13