Законы релятивистской механики

ЛЕКЦИЯ 21

Преобразования Лоренца оставляют неизменной величину

,

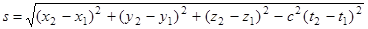называемую интервалом. Ее можно рассматривать как расстояние между двумя точками в четырехмерном пространстве (пространство Минковского) с координатами

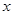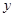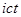, , , , где .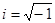

Для двух инерциальных систем отсчета 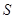и 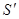, аналогичных тем, что мы рассмотрели в предыдущей лекции, с помощью преобразований Лоренца можно получить формулу сложе-ния скоростей в релятивистской механике:

, , .

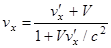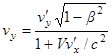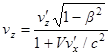При 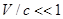эти выражения переходят в классическую формулу сложения (лекция 1). В случае 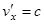получаем 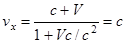. Этот результат является выражением постулата о постоянстве скорости света во всех инерциальных системах отсчета.

Можно показать, что импульс, определяемый классической формулой 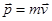не сохраняется в релятивистской механике. Для выполнения закона сохранения нужно использовать следующее определение релятивистского импульса:

,

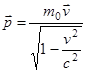Под 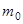здесь понимается так называемая масса покоя, которую имеет тело при 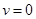, то есть обычная классическая масса. Физический смысл этой величины мы рассмотрим далее.

Второй закон Ньютона обобщается на случай релятивистского движения следующим образом:

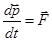, или .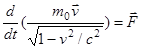

Релятивистский импульс можно выразить в ви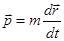де

, где 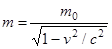- релятивистская масса.

Если ввести “собственное время”

,

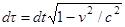то можно представить 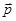в классической форме записи

.

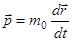В релятивистской динамике вводится важная величина 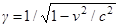, называемая релятивистским фактором. При этом релятивистский импульс можно выразить как 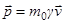. В случае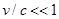 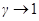и уравнения релятивистской динамики переходят в классические законы Ньютона. При скоростях тел, близких к скорости света .

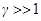Рассмотрим теперь выражение для релятивистской энергии. Его можно получить посред-ством вычисления элементарной работы силы (лекция 5)

.

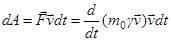После несложных преобразований можно получить

.

Константа 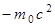добавлена для того, чтобы кинетическая энергия 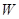обращалась в нуль при 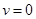. Таким образом релятивистская кинетическая энергия

.

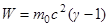При 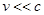она переходит в классическое выражение .

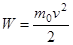Величина 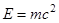называется полной релятивистской энергией тела, а величина 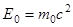- энергией покоя тела. Энергия покоя отражает глубокую физическую связь между массой тела и энергией, содержащейся в нем. Она может изменяться в ядерных взаимодействиях. Так происходит, например, при образовании ядер из отдельных нуклонов (дефект массы ядер). При этом полная релятивистская энергия замкнутой системы сохраняется.

Дата добавления: 2013-12-13