
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ламинарное и турбулентное течения. Движение тел в жидкостях и газах
|
|
|
|
ЛЕКЦИЯ 26
Ламинарное течение – течение жидкости, в котором можно указать точное значение скорости в данной точке в данный момент времени (можно построить линии тока).
Турбулентное течение – течение жидкости, в котором скорость в данной точке изменяется со временем беспорядочным образом (нельзя построить линии тока).
Так же, как и в предыдущей лекции, будем считать, что все сказанное о свойствах жидкости относится и к газу.
Рейнольдс экспериментально установил, что переход от ламинарного течения к турбулент-ному определяется значением безразмерной величины
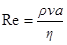 ,
,
называемой числом Рейнольдса. Здесь 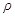 ,
, 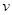 - плотность и скорость жидкости соответст-венно,
- плотность и скорость жидкости соответст-венно, 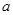 - характерный поперечный размер потока,
- характерный поперечный размер потока,  - коэффициент вязкости жидкости. Существует некоторое критическое значение числа Рейнольдса
- коэффициент вязкости жидкости. Существует некоторое критическое значение числа Рейнольдса 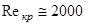 . При
. При  течение является ламинарным, а при
течение является ламинарным, а при  - турбулентным.
- турбулентным.
Понятие числа Рейнольдса связано с так называемым методом подобия, играющем важную роль в гидродинамике. Оказывается, что совершенно различные по своим параметрам потоки, обладающие одинаковым числом Рейнольдса, не только имеют одинаковый тип течения, но обладают и другими одинаковыми свойствами. Это обстоятельство, например, позволяет по результатам обдува в аэродинамической трубе макета самолета малых размеров получать информацию о технических параметрах реального самолета.
Рассмотрим обтекание твердого тела потоком жидкости или газа. Вблизи поверхности тела взаимодействие его молекул с молекулами жидкости приводит к “прилипании” жидкости к поверхности твердого. Если характеризовать это явление более строго, то речь идет о существо-вании слоя вблизи поверхности, в котором скорость жидкости относительно тела изменяется от нуля до скорости основного потока (рис. 1). Он называется пограничным слоем, а ширина соответ-ствующей области его эффективной толщиной. К потоку вне пограничного слоя можно применить теорему Бернулли. Из распределения линий тока на рис. 1 видно, что 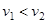 и
и  . Значит
. Значит 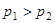 и
и  . По этой причине позади тела возникает сила разности давлений, закручивающая траектории частиц в верхней части пограничного слоя. Это приводит к явлению отрыва, при котором пограничный слой отрывается от задней части тела и в виде хаотических вихрей уносится потоком жидкости. Движение этих вихрей является турбулентным и область их локализации позади тела назы-вается турбулентным следом. Из-за большой скорости вихревого движения давление в этой области ниже давления перед телом, что приводит к добавочной силе сопротивления. Чем уже турбулентный след, тем меньше эта сила. Поэтому быстро движущимся в жидкостях и газах телам придают обтекаемую форму.
. По этой причине позади тела возникает сила разности давлений, закручивающая траектории частиц в верхней части пограничного слоя. Это приводит к явлению отрыва, при котором пограничный слой отрывается от задней части тела и в виде хаотических вихрей уносится потоком жидкости. Движение этих вихрей является турбулентным и область их локализации позади тела назы-вается турбулентным следом. Из-за большой скорости вихревого движения давление в этой области ниже давления перед телом, что приводит к добавочной силе сопротивления. Чем уже турбулентный след, тем меньше эта сила. Поэтому быстро движущимся в жидкостях и газах телам придают обтекаемую форму.
Движение тел в жидкостях и газах.
Рассмотрим равномерное движение шара радиуса 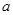 в жидкости со скоростью
в жидкости со скоростью 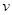 . Применим метод подобия и связанный с ним метод размерностей. Он состоит в следующем. Из пара-метров
. Применим метод подобия и связанный с ним метод размерностей. Он состоит в следующем. Из пара-метров 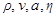 нужно составить величину размерности силы, зависящую от числа Рей-нольдса
нужно составить величину размерности силы, зависящую от числа Рей-нольдса  . Ее можно представить в виде
. Ее можно представить в виде
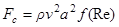 .
.
Для нахождения конкретного вида функции 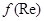 необходимо использовать дополнитель-ную информацию. Из опыта известно, что при малых скоростях
необходимо использовать дополнитель-ную информацию. Из опыта известно, что при малых скоростях  . Это дает
. Это дает
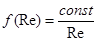 ,
, 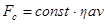 .
.
Более точный расчет дает значение  (формула Стокса). Теперь мы можем строго определить, что понимается в этом случае под малой скоростью. Ее можно считать малой, если
(формула Стокса). Теперь мы можем строго определить, что понимается в этом случае под малой скоростью. Ее можно считать малой, если  .
.
При  можно пренебречь вязкостью
можно пренебречь вязкостью  и зависимостью от числа Рейнольдса. Тогда выражение для силы сопротивления принимает вид
и зависимостью от числа Рейнольдса. Тогда выражение для силы сопротивления принимает вид
 .
.
Эксперимент показывает, что при больших скоростях движения тел в жидкостях и газах такая зависимость действительно имеет место.
Силы, действующие на крыло самолета.
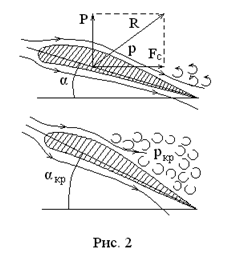
При обтекании крыла потоком воздуха давление над крылом меньше, чем под ним. В результате возникает подъемная сила крыла самолета  (рис. 2). Турбулентный след позади крыла приводит к силе лобового сопротивления
(рис. 2). Турбулентный след позади крыла приводит к силе лобового сопротивления  . Сумма этих сил создает равнодействующую силу
. Сумма этих сил создает равнодействующую силу  . Угол
. Угол 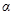 между плоскостью крыла и горизонтом называется углом атаки. Сначала, при увеличении угла атаки давление под крылом понижается и подъемная сила возрастает. При достижении критического угла атаки
между плоскостью крыла и горизонтом называется углом атаки. Сначала, при увеличении угла атаки давление под крылом понижается и подъемная сила возрастает. При достижении критического угла атаки 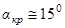 подъемная сила начинает падать. При этом в завихрен-ном пространстве над крылом давление ниже, чем в набегающем потоке, но выше, чем в случае полного обтекания крыла.
подъемная сила начинает падать. При этом в завихрен-ном пространстве над крылом давление ниже, чем в набегающем потоке, но выше, чем в случае полного обтекания крыла.
Жуковским и Чаплыгиным была построена теория обтекания крыла самолета на основе модели идеальной жидкости, в которой силы вязкости влияют лишь на создание кругового движения воздуха вокруг крыла. Такое движение было названо циркуляцией.
Рассмотрим важный частный случай.
Обтекание вращающегося цилиндра.
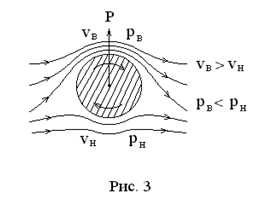 Пусть вращающийся вокруг собственной оси цилиндр обтекается потоком жидкости (или газа). Слои жидкости вблизи его поверхности вращаются вместе с ним. Для выбранных направлений движения на рис. 3 суммарная скорость потока сверху больше соответствую-щей скорости снизу. Тогда разность давлений создает подъемную силу, действующую на цилиндр снизу вверх. Это явление называется эффектом Магнуса. На нем основаны “крученые” удары футболистов и теннисистов.
Пусть вращающийся вокруг собственной оси цилиндр обтекается потоком жидкости (или газа). Слои жидкости вблизи его поверхности вращаются вместе с ним. Для выбранных направлений движения на рис. 3 суммарная скорость потока сверху больше соответствую-щей скорости снизу. Тогда разность давлений создает подъемную силу, действующую на цилиндр снизу вверх. Это явление называется эффектом Магнуса. На нем основаны “крученые” удары футболистов и теннисистов.
Теория Жуковского и Чаплыгина позволяет вычислить подъемную силу крыла самолета без учета сил вязкого трения. В ней сначала находится распределение скоростей вокруг крыла с учетом циркуляции воздуха подобно эффекту Магнуса. Затем по этому распределению с помощью уравнения Бернулли вычисляется подъемная сила. Циркуляция вокруг крыла действительно существует. Ее возникновение объясняется законом сохранения момента импульса (рис. 4). При отрыве вихря в задней части крыла образуется циркуляция вокруг крыла в противоположном направлении. Если считать, что до отрыва вихря полный момент импульса равнялся нулю, то должно выполняться равенство

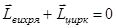 .
.
Процесс образования вихрей и возникновения циркуляции периодически повторяется. В результате создается постоянно действующая подъемная сила крыла самолета.
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 1117; Нарушение авторских прав?; Мы поможем в написании вашей работы!