Лекция 16

Раздел 7. Элементы механики твердого тела

Раздел 6. Элементы релятивистской динамики

Раздел 5. Механические колебания

Раздел 4. Закон сохранения момента

Движения (импульса) и энергии.

Раздел 3. Законы сохранения количества

Раздел 2. Работа, энергия, мощность

Варианты задач

Связь между энергией и импульсом релятивистской частицы

Кинетическая энергия релятивистской частицы

Полная энергия релятивистской частицы

Энергия покоя частицы

Релятивистский импульс частицы

Релятивистское изменение времени

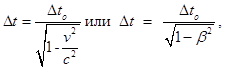
где Dt_o - собственное время, измеренное в состоянии покоя.

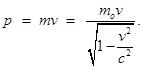
E_o = m_oc².

.

.

/

13 14

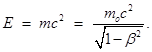
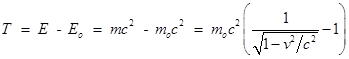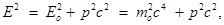
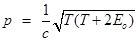Раздел 1. Кинематика и динамика

материальной точки и твердого тела

1. Уравнение движения материальной точки вдоль оси Х имеет вид: x = At² + Bt + C, где А = 1 м/с²; В = 3 м/с; С = 0. Определить координату x, мгновенную скорость v, ускорение а в момент времени t = 3 с. Найти среднюю скорость материальной точки в первые 3 с движения. Построить графики зависимости координаты x и скорости v от времени t.

2. Определить полное ускорение а точки, находящейся на ободе маховика радиусом r = 0,2 м, который вращается вокруг неподвижной оси согласно уравнению j = At³ + Bt² + С, где А = 1 рад/с³, В = 3 рад/с², С = 5 рад, в момент времени t = 2 с.

Найти среднюю угловую скорость вращения маховика в первые 2 с движения.

3. Радиус-вектор частицы изменяется со временем по закону r = Аt^2×i + Вt×j + С×k, где А = 2 см/с², В = 3 см/с, С = 1см. Определить скорость v и ускорение a, а также модуль скорости частицы в момент времени t = 1 с.

4. Зависимость угла поворота радиуса вращающегося колеса от времени дана уравнением j = A + Bt + Сt³, где А = 4 рад, В = 5 рад/с, С = -1 рад/с³. Найти в конце первой секунды вращения угловую скорость колеса, а также линейную скорость и полное ускорение точки, лежащей на ободе колеса. Найти среднюю угловую скорость вращения колеса за это время. Радиус колеса равен 20 см.

5. Тело массой 2 кг движется с ускорением, изменяющимся по закону a = 5t - 10. Определить силу, действующую на тело через 5 с после начала действия силы, и скорость тела в конце пятой секунды.

1. Из залитого подвала, площадь пола которого равна 50 м², требуется выкачать воду на мостовую. Глубина воды в подвале 1,5 м, а расстояние от верхнего уровня воды до мостовой 5 м. Найти наименьшую работу, которую необходимо затратить на откачку воды.

2. Вычислить работу А, совершаемую при равноускоренном подъеме строительной конструкции массой m = 0,5 т на высоту h = 10 м в течение времени t = 3 с. Сравнить величину А₁ с работой А₂, совершаемой при равномерном подъеме той же конструкции.

3. Подъемный кран за время t = 6 ч поднимает 6 000 т строи­тельных материалов на высоту h = 10 м. Найти мощность крана, если его КПД h = 0,7.

4. Под действием силы F =4t×i+ 3t×j (Н) тело массой m = 1кг начинает двигаться. Найти зависимость мощности N(t), развиваемой силой, от времени t и величину N для момента времени t = 2с.

5. Сплошной цилиндр соскальзывает без вращения с наклонной плоскости высотой h = 1 м, а затем скатывается с той же наклонной плоскости. Определить линейные скорости центра тяжести цилиндра в конце пути для обоих случаев. Трением пренебречь.

6. Обруч и сплошной шар, имеющие одинаковую массу m = 1 кг, катятся без скольжения с одинаковой скоростью v = 4 м/с. Найти кинетические энергии этих тел.

1. При выстреле снаряд получает кинетическую энергию 25 МДж. Масса снаряда 50 кг, масса ствола орудия 2 000 кг. Вычис

15 16

лить, какую кинетическую энергию получает ствол орудия вследствие отдачи.

2. На платформу массы m₁ = 0,5 т с помощью транспортера подают мешки с цементом. Определить скорость v₁, которую приобретает платформа в результате падения с транспортера мешка цемента массы m₂ = 50 кг со скоростью v₂ = 2 м/с, направленной под углом a = 60° к горизонту. Трением пренебречь.

3. Для очистки гладких гранитных поверхностей зданий используют струю песка, в которой песчинки движутся с постоянной скоростью v = 10 м/с и попадают на поверхность стенки под углом a = 45°. Определить импульс p, полученный стенкой при ударе одной песчинки массы m = 0,01 г.

4. Определить коэффициент полезного действия h при ударе молотка, забивающего гвоздь в стенку, если масса молотка m ₁ = 1,5 кг, а масса гвоздя m₂ = 30 г.

количества движения (момента импульса)

1. Шарик, прикрепленный к невесомой нити, вращается в горизон­тальной плоскости вокруг вертикальной оси. Определить, во сколько раз увеличится число оборотов шарика в единицу времени и его кинетическая энергия, если уменьшить длину нити в два раза, приблизив тем самым шарик к оси вращения.

2. Шарик, прикрепленный к невесомой нити, вращается в горизонтальной плоскости вокруг вертикальной оси. Во сколько раз увеличится число оборотов шарика в единицу времени и его кинетическая энергия, если его момент инерции уменьшить в 9 раз?

3. Чему равна масса шарика, вращающегося на нити вокруг вертикальной оси с частотой n₁ = 2 об/с, если человек, укорачивая нить с 50 см до 30 см, совершил работу А = 0,36 Дж?

4. Шарик, прикрепленный к невесомой нити, вращается в горизонтальной плоскости вокруг вертикальной оси. Во сколько раз надо укоротить нить, чтобы совершить работу А₂ = 1,6 Дж, если при укорачивании нити в 2 раза совершена работа А₁ = 0,6 Дж?

1. Написать кинематическое уравнение гармонических колебаний, совершаемых материальной точкой, если величина максимального смещения x _max = 8 см, максимальная скорость v _max = 16 см/с, начальная фаза колебаний j ₀ равна нулю. Вычислить максимальное ускорение a _max и максимальную возвращающую силу F _max, если масса материальной точки m = 0,1 кг.

2. Материальная точка массой m = 5 г совершает гармонические колебания, описываемые уравнением x = Asinw, где А = 10 см, w = p/4 c^-1. Вычислить величину возвращающей силы F и полную энергию материальной точки через 2 секунды после начала колебаний.

3. Стержень длиной l = 0,3 м колеблется около горизонтальной оси, перпендикулярной стержню и проходящей через его конец. Вычислить период Т колебаний стержня.

4. Однородный диск радиусом R = 0,4 м колеблется около горизонтальной оси, перпендикулярной плоскости диска и проходящей через одну из крайних точек диска. Определить период Т колебаний диска.

5. Тонкий обруч радиусом R = 25 см висит на стержне, закрепленном в стенке, и совершает гармонические колебания в вертикальной плоскости. Найти период Т колебаний обруча.

1. В лабораторной системе отсчета пи-мезон пролетел расстояние l = 70 м со скоростью v = 0,99×c за время Dt с момента рождения пи-мезона до момента его распада. Определить собственное время Dt_o жизни пи-мезона.

2. Фотонная ракета движется относительно Земли со скоростью v = 0,8×с. Во сколько раз замедлится ход времени в ракете с точки зрения земного наблюдателя?

3. Прямоугольный брусок со сторонами, равными 4 и 6 см, движется параллельно большей из сторон. При какой скорости движения брусок превратится в куб?

4. Определить, как изменится масса m релятивистской частицы, движущейся со скоростью v = 0,4×с, по сравнению с массой покоя m_o.

5. Два нейтрона движутся навстречу друг другу со скоростями 0,8×с и 0,6×с относительно Земли. Найти их относительную скорость.

(маятник Обербека)

1. Чему равен момент инерции маятника Обербека, если груз массой m = 785 г падает с высоты h = 1,5 м за время t = 10,5 с? Радиус шкива r = 23 мм. Ускорение свободного падения принять равным 9,81 м/с². Во сколько раз уменьшится момент инерции маятника, если грузы массой m₁ = 145 г каждый переместить с концов стержней к центру, установив их на расстоянии (2/3) l от центра? Длина стержней l = 0,3 м.

2. Чему равен момент инерции маятника Обербека, если груз массой т = 790 г опустился со средней скоростью <v> = 0,15 м/с за время t = 11 с? Радиус шкива r = 23 мм; ускорение свободного падения принять равным 9,81 м/с. Во сколько раз уменьшится момент инерции маятника Обербека, если грузы переместить с концов стержней на середину? Масса каждого груза m₁ = 145 г, длина стержней l = 0,3 м.

3. Каков момент инерции маятника Обербека, если груз массой m = 760 г опустился за время t = 10,5 с и привел во вра­щение маятник со средней угловой скоростью <w> = 6,2 с^-1? Радиус шкива r = 23 мм. Ускорение свободного падения принять равным 9,81 м/с. На каком расстоянии от оси вращения закреплены на стержнях грузы массой m₁ = 145 г каждый, если момент инерции, обусловленный ими, составляет 25% момента инерции маятника?

	17 18

Дата добавления: 2013-12-13