
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение вектора. 2. Линейные операции над векторами и их свойства ..5
|
|
|
|
I. Векторная алгебра
ОГЛАВЛЕНИЕ
ТЕОРИЯ
I. Векторная алгебра
1. Определение вектора…………………………………………………………………..……5
2. Линейные операции над векторами и их свойства………………………………………..5
3. Базис и координаты…………………………………………………………………………6
4. Скалярное произведение векторов…………………………………………………………9
5. Векторное произведение векторов………………………………………………………..10
6. Смешанное произведение векторов………………………………………………………12
II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
1. Уравнения поверхностей и линий…………………………………………………………14
2. Плоскость в пространстве………………………………………………………………….15
3. Прямая линия в пространстве……………………………………………………………...20
4. Прямая и плоскость…………………………………………………………………………23
III.АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
1. Простейшие задачи на плоскости…………………………………………………………...25
2. Прямая линия на плоскости…………………………………………………………………25
3. Кривые второго порядка……………………………………………………………………..28
4. Преобразования координат…………………………………………………………………..33
5. Линии в полярной системе координат……………………………………………………....38
6. Параметрическое задание линий…………………………………………………………….42
IV. Поверхности второго порядка……………………………………………..........43
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ…………………………………………………………………..50
Задания для самостоятельной работы
Домашние задания……………………………………………………………………………...108
Расчетная работа………………………………………………………………………………..125
образцы контрольных работ…………………………………………………………151
Основные определения и формулы……………………………………………….152
БИБЛИОГРАФИЧЕСКИЙ СПИСОК………………………………………………………….172
Понятие вектора возникло как математическая абстракция объектов, характеризующихся не только скалярной величиной, но и направлением, например: перемещение, скорость, напряженность электрических и магнитных полей.
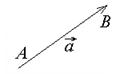
Вектором называется направленный отрезок прямой, у которого один конец (точка 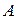 ) называется началом вектора, а другой конец (точка
) называется началом вектора, а другой конец (точка 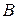 ) – концом вектора.
) – концом вектора.
Вектор обозначается либо значком 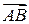 , либо одной строчной буквой
, либо одной строчной буквой 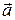 .
.
Вектор, начало и конец которого совпадают, называется нулевым вектором: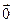 . Нулевому вектору приписывают любое направление.
. Нулевому вектору приписывают любое направление.
Вектор характеризуется модулем (или длиной), который равен длине отрезка 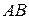 :
: 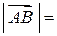
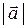 .
.
Вектор 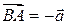 называется противоположным ненулевому вектору
называется противоположным ненулевому вектору 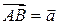 .
.
Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.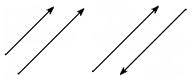
Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и направление.
 Точка приложения вектора может быть выбрана произвольно, векторы иногда называют свободными.
Точка приложения вектора может быть выбрана произвольно, векторы иногда называют свободными.
Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.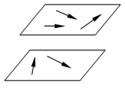
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 379; Нарушение авторских прав?; Мы поможем в написании вашей работы!