По модулю скорости. Опыт Ламмерта

В настоящее время известны несколько опытов, в которых проверялось распределения частиц идеального газа по модулю их скоростей. Они использовали метод молекулярных и атомных пучков (Штерн 1920 г., Элдридж 1927 г., Ламмерт 1929 г.). Возможна также проверка распределения Максвелла по наблюдению уширения спектральных линий, которые излучают движущиеся возбужденные молекулы газа. За счет эффекта Доплера происходит смещение частоты излучения в зависимости от скорости движения молекул, что и позволяет по уширению спектральных линий проверить распределение молекул по скоростям.

Рассмотрим подробнее опыт Ламмерта. В специальном устройстве испаряют жидкий металл, его пары содержат молекулы с различными скоростями, которые соответствуют температуре испаряемого металла. Затем формируется узкий молекулярный пучок, он проходит через систему, состоящую из двух синхронно вращающихся с угловой скоростью 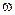дисков, расположенных на расстоянии 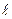друг от друга (рис. 2.6,а). В этих дисках имеются радиальные щели, смещенные на некоторый угол 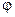друг относительно друга. Через такую систему из двух дисков проходят молекулы, скорости которых удовлетворяют условию, при котором время прохождения молекулой расстояния 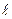между дисками должно равняться времени поворота дисков на угол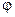

. (2.31)

Эти молекулы, пройдя систему из двух дисков, попадают в ловушку (приемник).

Таким образом, выделяются из пучка только те молекулы, скорости которых попадают в узкий интервал скоростей (этот интервал связан с конечной шириной щелей, он будет вблизи скорости 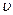, равной ). Число таких молекул можно было оценить по толщине осадка на стеклянной пластине, помещенной в приемнике. Изменяя параметры 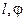и 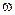, можно было установить распределение молекул пучка по скоростям. Полученные из опыта кривые распределения молекул по скоростям подтвердили справедливость распределения Максвелла.

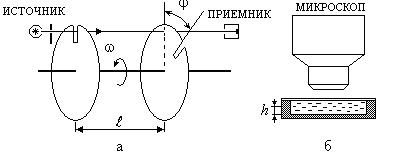
Рис. 2.6

*2.8. Опыты Перрена по определению постоянной Авогадро

Известно, что броуновские частицы (мельчайшие частицы твердого вещества, взвешенные в жидкости или газе и которые можно наблюдать в микроскопе) находятся в тепловом движении так же, как и молекулы. Поэтому Перрен предположил, что распределение Больцмана справедливо и для броуновских частиц. При этом из-за значительно большей массы этих частиц по сравнению с массой молекул должны были наблюдаться более существенные изменения в концентрации частиц при малом изменении высоты . В своих опытах Перрен использовал микроскоп с малой глубиной резкости. Это позволило ему достаточно хорошо наблюдать частицы (их размеры были порядка ) в пределах объема, высота которого была порядка ().

В опытах определялось число частиц, попадающих в поле зрения микроскопа в зависимости от высоты , отсчитываемой от дна стеклянной трубки, в которой находилась жидкость с взвешенными в ней броуновскими частицами (рис. 2.6,б).

В соответствии с распределением Больцмана для отношения концентраций частиц на разной высоте (формула (2.29)) можно записать

,

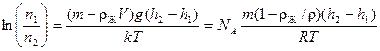что позволило получить формулу для экспериментального определения постоянной Авогадро

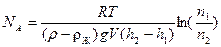. (2.32)

В эти формулы вместо массы 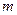частицы входит разность (), учитывающая дополнительную силу - силу Архимеда, действующую в жидкости на частицу; - плотности жидкости и вещества частицы соответственно; 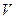- объем частицы.

В результате проведенных опытов Перрен показал, что постоянная Авогадро может принимать значения 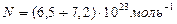, заключенные в интервале, что находилось в согласии с данными других опытов.

Уникальность опытов Перрена была связана с плохой экспериментальной аппаратурой, существовавшей в то время (1906 г.). Так, в частности, достаточно трудно было поддерживать с высокой точностью температуру во всем объеме жидкости и наблюдать быстро движущиеся частицы в микроскопе.

Дата добавления: 2013-12-13