Энтропия в термодинамике

Ряд термодинамических формулировок второго начала термодинамики содержит понятие энтропии системы. При развитии термодинамики оказалось, что помимо внутренней энергии системы функцией состояния системы также является величина, которая для равновесных процессов вводится (это было сделано Клаузиусом) по формуле

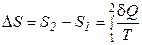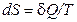, . (2.45)

Следовательно, эта величина не зависит от пути перехода из одного состояния в другое, она получила название энтропия (энтропия в переводе с греческого - поворот, превращение). Величину (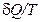) в формуле (2.45) называют приведенной теплотой.

Из формулы (2.45) следует, что источником изменения энтропии системы является теплообмен между системой и внешними телами. В зависимости от вида равновесного процесса, происходящего в системе, энтропия системы может как возрастать (тепло подводится к системе), так и убывать (тепло отводится от системы).

Оказалось, что существует еще один источник изменения энтропии, он связан с протеканием в системе неравновесного процесса. Клаузиус показал, что при протекании неравновесного процесса в замкнутой (изолированной) системе ее энтропия возрастает. Поэтому для изменения энтропии системы с учетом возможности протекания в ней неравновесного процесса равенство (2.45) запишется следующим образом:

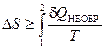. (2.46)

Эта формула (2.46) является важной для анализа протекания необратимых процессов в замкнутых (или изолированных) системах (нет теплообмена между системой и окружающими телами - ), для них .

Дадим формулировку второго начала термодинамики с использованием понятия энтропии (Клаузиус): энтропия замкнутой системы стремится к максимуму:

. (2.47)

Из опыта известно, что если замкнутая (или изолированная) система сначала находилась в неравновесном состоянии, то с течением времени в ней протекают процессы перехода в равновесное состояние, в состояние теплового равновесия. При таком процессе энтропия системы возрастает (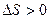, рис. 2.10,а). Когда система переходит в равновесное состояние, энтропия достигает максимального значения, которое с течением времени остается неизменным

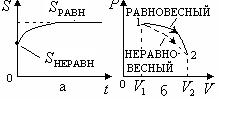(, рис. 2.10,а). Следовательно, в таких системах невозможен процесс перехода системы из равновесного состояния в неравновесное, так как при этом энтропия будет убывать, что запрещено вторым началом термодинамики. Отсюда следует, что важное свойство энтропии системы – помимо того, что она является функцией состояния, она также определяет направление протекания процессов в замкнутых системах.

Наиболее полно физический смысл энтропии раскрывается в статистической (молекулярной) физике.

Рис.2.10

В дальнейшем будут даны формулировки второго начала термодинамики с точки зрения молекулярного строения вещества.

Дата добавления: 2013-12-13