
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Использование разновременных ЛП
|
|
|
|
РАЗДЕЛ 5
Вопросы для самопроверки
1. Что дает на поверхности Земли значение навигационного параметра?
2. Изолинии и их форма и уравнения для различных параметров.
3. В чем состоит сущность ОМС методом изолиний?
4. Какие общие способы решения задачи ОМС применяют в море?
5. Что такое градиент изолинии и как его рассчитывают?
6. Что такое линия положения (ЛП), её параметры и уравнение?
7. Какие способы ОМС по ЛП применимы в судовождении?
8. Средняя квадратическая погрешность (СКП) ЛП, её свойства и величины.
9. Какие способы оценки точности места судна применимы в судовождении?
10. Радиальная СКП места судна, способы её расчетов и применения.
11. Назначение избыточных измерений навигационных параметров.
12. Веса ЛП и их использование при ОМС.
13. Фигура погрешности при избыточном числе ЛП и сущность вероятнейшего места судна.
14. Как влияют систематические погрешности на ОМС?
15. Как используют центрографический и штурманский метод получения вероятнейшего места судна?
16. Различные способы аналитического решения задачи ОМС.
17. Как аналитически рассчитывают точность места судна?
18. Какое значение имеют таблицы МТ-2000 для решения задач математических основ судовождения?
5.1 Общий случай решения основной задачи судовождения
Практически все измерения навигационных параметров, которые выполняются для ОМС одним наблюдателем, всегда бывают разновременными. Условно все измерения, выполненные одним наблюдателем в быстрой последовательности считаются одновременными.
При движении судна разновременные измерения выполняются в различных точках и должн6ы быть приведены к одному моменту и месту судна. Однако такое приведение осуществляется переносом изолиний или линий положения е нужному моменту и месту судна лишь по счислению. Неточности счисления при значительных интервалах между измерениями существенно снижает точность переносимых линий и, естественно приводит к снижению точности ОМС.
Указанное выше снижение точности обсерваций при обычных крюйс-методах, заставляло судоводителей искать методы ОМС по разновременным измерениям, которые дают место судна независимое от ошибок счисления. Частные случаи такого решения задач под названием исправленного и двойного крюйс-пеленга давно и успешно применялись на флоте. Решение задачи в общем виде было предложено академиком А.Н. Крыловым и впервые с достаточным теоретическим обоснованием приведено в [10. –С. 509 - 539]. Как это так и другие навигационные пособия [1],[3],8] рассматривают общее решение задачи очень усложненно или чрезвычайно упрощенно. Наиболее полно и просто решение задачи для любых условий измерений приведено в [7], где по методике М.Н. Андреева показано решение основной задачи судовождения с помощью сопутствующих линий положения (СЛП).
Основной задачей судовождения является не только ОМС, но также определение элементов движения судна, о чем говорилось в первом разделе данного конспекта. Иными словами, в наиболее общем виде основною задачей судовож
дения является определение места судна, направления и скорости его перемещения по земной поверхности.
Уравнение равномерного и прямолинейного движения судна в прямоугольной системе координат j и l(w) при известных скорости u и интервале времени t запишется так:
j=jо+ujt l=lо+uw•t, (5.1)
где uj та uw - проекции вектора движения судна на координатные оси за промежуток времени t.
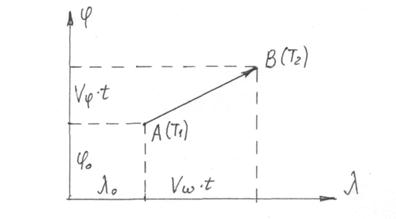
|
Рис.5.1 Движение судна в прямоугольной системе координат
По уравнению (5.1) видно что для решения задачи необходимо знать четыре величины: координаты начала движения величину и направление вектора движения судна или его проекции на координатные оси. Для решения необходимо как минимум четыре уравнения. В общем случае это могут быть уравнения четырех изолиний с параметрами U1, U2, U3,U4,, которые должны быть разновременными. Они имеют вид:
U1=f1(j1, l1)
U2=f2(j2, l2)
U3=f3(j3, l3)
U4=f4(j4, l4)
Выразив текущие координаты через начальные и их приращения на протяжении интервала t, получим уравнения изолиний:
U1=f1(j0, l0)
U2=f2(j0+ujt21; l0+uwt21)
U3=f3(j0+ujt31; l0+uwt31)
U4=f4(j0+ujt41; l0+uwt41),
Где t21=T2-T1, t31=T3-T1; t41=T4-t1
Решения этих уравнений относительно неизвестных величин в общем виде приведет к уравнениям:
j0=j1(U1, U2, U3, U4, t21, t31, t41)=K1
l0=j2(U1, U2, U3, U4, t21, t31, t41)=K2
uj=j3(U1, U2, U3, U4, t21, t31, t41)=К3 (5.2)
uw=j4(U1, U2, U3, U4, t21, t31, t41)=K4
Текущие координаты места судна на любой момент времени с учетом уравнений (5.1) прнимают вид:
j=K1+K3t
l=K2+K4t
Непосредственное решение уравнений (5.2) при достаточно сложных функциональных зависимостях f1, f2, f3, f4, а также и уравнений изолиний, представля
ет трудную задачу даже при использовании вычислительной техники. Геометрический смысл определения линии равномерного и прямолинейного движения судна, деленного на отрезки пропорциональные интервалам времени t21, t31, t41 Показаны ниже.
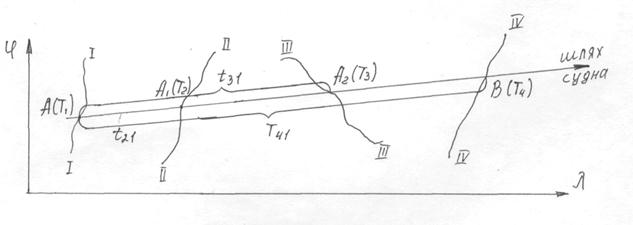
|
Рис. 5.2 Графическое решение основной задачи судовождения
Графоаналитическое решение основной задачи судовождения разработанное до практического применения в условиях ходового мостика пока что только для условий равномерного прямолинейного движения судна. Исследования по теоретическому и практическому обоснованию решения основной задачи судовождения при неравномерному и криволинейному движении судна ожидают своих авторов.
5.2 Метод исправленного крюйс-пеленга.
Этот метод, является частным случаем применения сопутствующей линии положения (СЛП). В принципе, этот подход возможен и для других типов изолиний или линий положения, например дистанции (крюйс-дистанция), но изолиния пеленга имеет самую простую форму и наглядность, поэтому остановимся именно на нём.
Этим методом, с достаточной точностью, можно определить все параметры движения судна (скорость, курс) и новое (или предыдущее) место судна, которое можно считать обсервованным.
Для определения этих параметров, необходимо знать – пеленг на маяк, обсервованное место судна, и дополнительная изолиния, причём последовательность получения этих параметров не важна. Условием использование метода, есть постоянство курса и скорости судна.

Риса. 5.3 Получение СЛП
Предположим, что судно движется с постоянной скоростью и курсом, точное значение которых несущественно. В один из моментов времени Т1 получено точ
ное (обсервованное) место судна М 1, следовательно, возможный путь судна (ВПС), можно проложить через эту точку.
В другой момент времени Т2, взят пеленг на маяк или получена какая-либо ЛП. За этот промежуток времени t21, судно, если бы действительно следовало этим курсом, пришло бы в точку М1 и прошло бы расстояние S21, предполагаемая скорость судна при этом была бы:

Очевидно, что в момент времени T3 за некоторый другой промежуток времени t32, следуя этой скоростью, судно вдоль ВПС прошло бы расстояние:
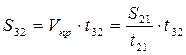
и попало бы в точку М3.
Теперь через эту же точку проведём другой ВПС', понятно, что в момент времени Т2, судно бы оказалось в точке М'2 и прошло бы расстояние S'21, предполагаемая скорость при этом была бы:
 ,
,
и за промежуток времени t32, следуя этой скоростью, судно вдоль ВПС' прошло бы расстояние:
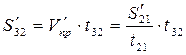
и попало бы в точку М'3.
Проведя через точки М3 и М'3 линию, мы увидим, что она параллельна сделанному пеленгу или ЛП, следовательно, можно сделать вывод, что на этой линии лежат все возможные места судна на момент T3 и, разумеется, истинное место.
Особенностью этой линии является то, что она перемещается вместе с судном, сопутствует ему, потому и названа – сопутствующей линией положения СЛП.
Если в момент T3 сделать наблюдение некоторой другой изолинии, например изобаты, то на пересечении с СЛП мы получим другое обсервованное место судна и через обе обсервованные точки, можем провести истинную линию пути судна, из которой можем получить скорость и курс.


Рис. 5.4 и 5.5 Получение пути судна с помощью СЛП
СЛП можно переносить не только вперёд по ходу судна, но и назад, на какую либо изолинию полученную ранее, например изостадию и получить место и все остальные параметры движения ранее полученной обсервации в момент времени Т0. Более того, построение полностью обратимо, то есть вначале можно измерить изолинию, потом снять пеленг и напоследок произвести обсервацию, затем на момент получения изолинии определить обсервованное место.
5.3 Общий случай СЛП.
Предположим, что получены три разновременные линии положения не пересекающихся в одной точке.
Судно двигаясь с постоянной скоростью и курсом, поочерёдно пересекает все три линии ЛПI, ЛПII и ЛПIII в моменты времени Т1, Т2 и Т3. Наша задача найти геометрическое место точек в которых может находиться судно в момент времени Т4. Можно доказать, что эти точки будут лежать на одной прямой, то есть нам достаточно получить, как минимум, две точки для её построения. Эта линия и будет СЛП(Т4).
В момент времени Т1 судно могло находиться в любой точке ЛПI и следовать любым курсом (нам не важно каким), одним из возможных курсов может быть курс вдоль ЛПI. Следуя этим курсом, судно в момент Т2 пересечёт ЛПII, а в момент Т3 ЛПIII, обозначим это расстояние – S32, рассчитаем скорость на этом промежутке, за время t32 = T3 – T2:
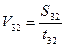 .
.
Двигаясь с этой скоростью дальше к моменту времени Т4, судно прошло бы расстояние  и оказалось бы в точке М41, лежащей на СЛП(Т4).
и оказалось бы в точке М41, лежащей на СЛП(Т4).
Аналогичные рассуждения можно провести и для ЛПII, и для ЛПIII и получить точки М42, М43, лежащие на СЛП(4). Если все три точки оказались на одной прямой, значит, наши построения верны.

Рис. 5.6 Построение СЛП в общем случае
Если в момент времени Т4, наблюдалась какая либо изолиния или ЛП, мы получим обсервованное место судна на это время, а применив рассуждения приведенные в 8.1, мы можем получить место судна в момент Т1, таким образом, зная две обсервованные точки, мы легко рассчитаем скорость и курс судна. В этом построении СЛП(Т4), поочерёдно пересекая все ЛП, вполне удовлетворяет всем требованиям возможного пути судна (ВПС).
5.4 Частные случаи применения СЛП
Самым характерным случаем, могут являться, три пеленга одного объекта сделанные последовательно.
В том случае точку пересечения всех линий можно считать принадлежащей любой СЛП, в частности СЛП(Т4). Нам осталось, получить только вторую точку для этой СЛП, для этого нам нужно проложить возможный путь судна (ВПС).

Рис. 5.7 СЛП и путь судна в частном случае
Для этого в удобном масштабе на ЛПI откладываются промежутки времени t32 = T3 – T2 и t31 = T3 – T1. Из конца отрезка t32 проводится линия параллельная ЛПIII до пересечения с ЛПII. Полученная точка и конец отрезка t31 соединяются прямой М1М2 и продолжается дальше до пересечения с ЛПIII в точке М3, полученные отрезки пропорциональны по построению промежуткам времени t31 и t32. Следовательно эта прямая является одним из возможных ВПС. Отложив на ВПС отрезок  , рассчитанный уже по известным принципам получим ещё одну возможное
, рассчитанный уже по известным принципам получим ещё одну возможное
место судна – точку М4, проведя через неё и точку пересечения всех ЛП прямую мы получим СЛП(Т4).
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 433; Нарушение авторских прав?; Мы поможем в написании вашей работы!