Развертки цилиндрических поверхностей

Пример 1.

Развертки конических поверхностей

Построение приближенных разверток развертывающихся поверхностей

Способ треугольников

Построение развертки боковой поверхности пирамиды, какие бы положения относительно плоскостей проекций ее ребра или основания не занимали, выполняется методом треугольников (метод триангуляции).

Пример 4. Построить развертку трехгранной пирамиды (рис.180, а).

В данном примере основание пирамиды расположено параллельно плоскости П₁, поэтому проекция основания A₁B₁C₁ равна натуральной величине треугольника. Боковые ребра пирамиды SA,SB,SC являются прямыми общего положения.

Для определения натуральных величин боковых ребер пирамиды, будет удобно вос- пользоваться дополнительными построения-

ми приведенными на рис.179 (метод прямоу- гольного треугольника).

Рис. 179  

Рис. 180

Развертка боковой поверхности пирамиды состоит из трех треугольников. Величину S ₀ и первое ребро S₀A₀ откладываем произвольно. Затем последовательно откладываем натуральные величины всех ребер пирамиды (рис.180, б).

Развертки всех развертывающихся поверхностей являются приближенными, т.к. их заменяют поверхностями вписанных многогранников с гранями в виде треугольников или четырехугольников.

Построить приближенную развертку боковой поверхности конуса Ф, заданного окружностью k и вершиной S (рис. 181).

Рис. 181  

Заменим поверхность конуса поверхностью пирамиды, вписанной в конус. Чем больше сторон в основании будет иметь пирамида, тем точнее будет развертка конуса. За основание пирамиды примем правильный двенадцатиугольник. Так как заданная поверхность Ф имеет плоскость симметрии, то и развертка будет иметь ось симметрии. На рис.181б выполнена только половина развертки – до оси симметрии S₀A₀.

Для построения приближенной развертки конуса выполняем следующие построения:

1. Выбираем произвольную точку S₀, проводим вертикальную прямую l ₀ и откладываем S₀A₀=AS, т.к. ребро AS||П₂, то S₂A₂=AS. Используем метод триангуляции.

2. На ребре A₀ S₀ достраиваем треугольник I₀ со сторонами S₀1₀ и S₀A₀. Натуральная величина стороны A₁ представлена на плоскости П₁ (A₁1₁=A₀1₀ – хорда, заменяющая дугу окружности).

Для определения натуральных величин боковых ребер пирамиды, они же являются обра-

зующими конической поверхности, необходимо использовать вспомогательные построения аналогичные тем, что были приведены на рис.179.

3. На развертке последовательно пристраиваем треугольники II₀, III₀…, которые соответствуют граням пирамиды II, III и т.д.

4. Полученную ломаную линию A_о1_о2_о3_оВ_о заменяем плавной кривой линией. Таким образом, мы построили приближенную развертку заданной конической поверхности.

Заменим поверхность цилиндра поверхностью n-гранной призмы, вписанной в цилиндрическую поверхность. Развертку цилиндра можно построить, используя как метод раскатки, так и метод нормального сечения, рассмотренные ранее (см. 3.1.2.).

Рис. 182

Заданную цилиндрическую поверхность рассекаем фронтально проецирующей плоскостью S(S₂), которая перпендикулярна образующей цилиндра (ребрам вписанной призмы).

Если цилиндрическую поверхность с нанесенной на ней линией нормального сечения разогнуть и совместить с плоскостью чертежа, то на развертке нормальному сечению будет соответствовать прямая k₀. На развертке точки верхнего и нижнего основания соединяем плавной кривой линией.

Контрольные задания по теме «Развертки поверхностей»

Задача 1. Построить развертку поверхности пирамиды (рис.183).

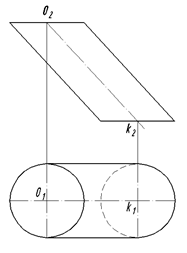
Задача 2. Построить развертку наклонного цилиндра (рис.184)

Рис. 183

Контрольные вопросы

1. Что называется разверткой поверхности?

2. Какие поверхности называются развертывающимися?

3. Укажите основные свойства разверток.

4. В чем отличие точной развертки от приближенной?

5. Метод триангуляции: область применения, суть способа.

6. Метод нормального сечения.

7. Метод раскатки.

Дата добавления: 2013-12-13