Эффект масштаба. Трансакционные издержки

Средние издержки. Предельные издержки.

Средние общие издержки можно получить путем деления общих издержек на количество выпущенной продукции:

АТС = TC/Q

или путем сложения средних постоянных (AFC) и средних переменных издержек (AVC):

АТС = AFC + AVC = (FC+VC) /Q.

Предельные издержки (marginal cost) - это приращение совокупных издержек, вызванное бесконечно малым увеличением производства. Под предельными издержками обычно понимают издержки, связанные с производством последней единицы продукции:

Из этой формулы видно, что постоянные издержки не влияют на величину предельных издержек. Предельные издержки — производная функция только от переменных издержек:

Предположим, что цены ресурсов остаются неизменными, тогда как бюджет производителя постоянно растет. Соединив точки пересечения изоквант с изокостами, мы получим линию OS – «путь развития» (аналогичную линии уровня жизни в теории поведения потребителя). Эта линия показывает темпы роста соотношения между факторами в процессе расширения производства. На схеме №1, например, труд в ходе развития производства используется в большей мере, чем капитал. Форма кривой «путь развития» находится в зависимости, во-первых, от формы изоквант и, во-вторых, от цен на ресурсы (соотношение между которыми определяет наклон изокост). Линия «путь развития» может быть прямой или кривой, исходящей из начала координат.

Если расстояния между изоквантами уменьшаются,это свидетельствует о том, что существует возрастающая экономия от масштаба, т.е. увеличение выпуска достигается при относительной экономии ресурсов (схема №1). Если расстояния между изоквантами увеличиваются, это свидетельствует об убывающей экономии от масштаба (схема №2).

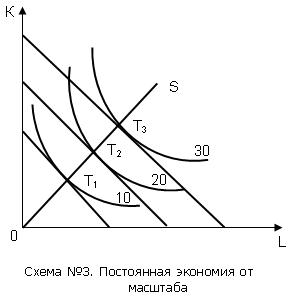
В случае, когда увеличение производства требует пропорционального увеличения ресурсов, говорят о постоянной экономии от масштаба (схема №3). Таким образом, изокванта позволяет не только экономно использовать имеющиеся ресурсы для достижения данного объема производства, но и определить минимально эффективный размер предприятия в отрасли. В случае возрастающей экономии от масштаба фирме необходимо наращивать объем производства, так как это приводит к относительной экономии имеющихся ресурсов. Убывающая экономия от масштаба свидетельствует о том, что минимально эффективный размер предприятия уже достигнут и дальнейшее наращивание производства нецелесообразно. Тем самым анализ выпуска с помощью изоквант позволяет определить техническую эффективность производства. Пересечение изоквант с изокостой позволяет определить не только технологическую, но и экономическую эффективность, т.е. выбрать технологию (трудо- или капиталосберегающую, энерго- или материалосберегающую и т.д.), позволяющую обеспечить максимальный выпуск продукции при тех денежных средствах, которыми располагает производитель для организации производства.

Дата добавления: 2013-12-13