Случайная функция

Понятие о случайных функциях и процессах

Параметры элементов и систем в связи с влиянием на них большого количества факторов на этапах разработки, производства и эксплуатации имеют случайный характер. Рассматривая эти параметры при конкретных значениях факторов, от которых они зависят, мы будем иметь эти параметры как случайные величины. Для более полного представления о функционировании системы в реальных условиях эксплуатации необходимо знать как изменяются её параметры при изменении влияющих факторов. Такое представление дают случайные функции.

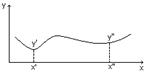Это функция, которая в результате опыта может принять тот или иной конкретный вид, но неизвестно заранее какой именно. Конкретный вид, принимаемый случайной функцией в результате однократного опыта, называется реализацией случайной функции.

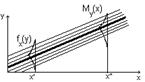
Если над случайной функцией провести группу опытов, то получим семейство реализаций этой функции. Это семейство можно рассмотреть при разных факторах x, т.е. в сечении семейства. В каждом сечении параметр y будет являться обычной случайной величиной, которая характеризуется законом распределения. Случайную функцию можно также определить, как функцию своего аргумента, значение которого при любом значении её аргумента является случайной величиной. Характеристиками случайных функций, в отличие от числовых характеристик случайной величины, представляющих собой определённые числа, являются в общем случае не числа, а функции (математическое ожидание, дисперсия, среднеквадратичное отклонение, автокорреляционные функции, взаимные корреляционные функции).

Математическое ожидание M[Y(x)] случайной функции Y(x) есть неслучайная функция m_y(x), которая при каждом значении аргумента x равна математическому ожиданию соответствующего сечения случайной функции.

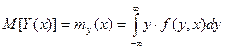, где f(y,x) – одномерная плотность вероятностей семейства реализаций случайных функций.

Дисперсия D[Y(x)] случайной функции Y(x) есть неслучайная функция D_y(x), значение которой для каждого x равно дисперсии соответствующего сечению случайной функции.

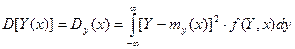
Дисперсия D_y(x) характеризует разброс реализаций в семействе относительно математического ожидания m_y(x). Равномерная плотность распределения f(Y,x) позволяет найти среднее значение случайной функции и её дисперсию, но не содержит никакой информации о поведении случайной функции.

Дата добавления: 2013-12-13