Определение среднего времени работы резервированной аппаратуры до отказа

Аналитическое сравнение общего и раздельного резервирования

Сравнение общего и раздельного резервирования

Для простоты будем считать, что все элементы в системе равнонадёжны, и отсутствует переключающее устройство, тогда:

;

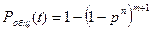Увеличим сложность системы при количестве резервных систем:

n → ∞ P_общ→ 0

P_разд→ 0

Количество элементов конечно

m → ∞ P_общ→ 1

P_разд→ 1

n → ∞ P_общ→ 0

m → ∞ P_разд→ 1

Выводы:

1. Общее резервирование целесообразно применять при сравнительно небольшом числе рабочих элементов в исходной системе, т.к. с ростом n надёжность систем резко падает;
2. При раздельном резервировании можно получить сколь угодно высокую степень надёжности при любом количестве элементов в исходной системе;
3. При раздельном резервировании можно резервировать только наиболее ненадёжные элементы и получить систему равной надёжности;
4. При общем резервировании меньше количество соединений;
5. При общем резервировании отсутствует большое количество согласующих устройств, которые требуется при постоянном раздельном резервировании.

;

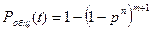Вероятности отказов:

;

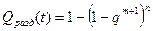
При q<<1 скобку (1-q)ⁿ можно разложить в ряд 1-nq, тогда:

;

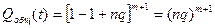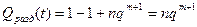
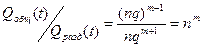; n=20; Pi=0,9; m=2

;

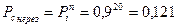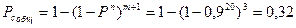
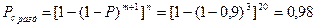
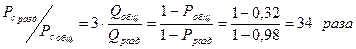
10.5. Расчёт надёжности при скользящем резервировании

Скользящее резервирование имеет место в том случае, когда система состоит из одинаковых блоков, и для их замены в случае отказа используются аналогичные резервные блоки или элементы.

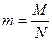
Система считается исправной, если работают все N каналов.

основная система

резервная система

Система откажет, если число отказавших блоков S>M. Для простоты возьмём Р_П=1, тогда:

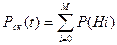; Hi – гипотеза, заключающаяся в том, что система исправно работает при отказе ровно i блоков; P(Hi) – вероятность этой гипотезы; М – максимальное число отказавших блоков, не приводящее к отказу системы в целом.

Вероятности гипотез подчиняются биноминальному распределению, если время безотказной работы каждого элемента подчиняется распределению Пуассона.

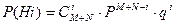(при небольших M и N)

10.6. Расчёт показателей надёжности резервированной аппаратуры по графу переходов

Графы переходов иллюстрируют процессы перехода изделия из одного состояния в другое в случайный момент времени. По графу переходов составляется система дифференциальных уравнений Колмогорова. Такой способ решения задачи анализов надёжности является единственным для резервированной ремонтируемой аппаратуры. По графу переходов можно определить все необходимые показатели надёжности системы: вероятность безотказной работы, среднюю наработку на отказ, среднее время восстановления, функцию и коэффициент готовности. Если в графе имеются n узлов, то среди них будет d узлов, соответствующих отказовым состояниям системы, и (n-d) узлов, отражающих рабочее состояние. Если рассматривается функционирование системы до некоторого l -того состояния (например до 1-го отказа) при определении P или Т_ср, то l -тое состояние называется поглощающим. Система, попавшая в l -тое состояние, уже не может перейти в другие, и в графе отсутствуют переходы из этого состояния в работающее. Вид графа переходов зависит от структуры системы (схемы расчёта надёжности), числа обслуживающих бега и дисциплины обслуживания – приоритета обслуживания, который может быть прямым, обратным и высшим.

Прямой приоритет – первым ремонтируется первый отказавший элемент;

Обратный приоритет – ремонт начинается с последнего отказавшего элемента;

Высший приоритет – указывается элемент, с которого начинается ремонт.

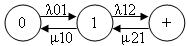
Рассмотрим систему, состоящую из 2-х элементов расчёта надёжности: основного и резервного. Может быть 2 ситуации:

1. Приоритет отказа имеет место
2. Отсутствует приоритет отказа

1 случай

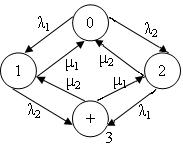
Решаем с преобразованием Лапласа и находим состояние P_i(t).

, где k – количество работоспособных состояний.

Поскольку сумма вероятностных состояний равна 1, то 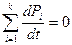, Это значит, что сумма правых частей системы уравнений всегда равна 0. Это свойство полезно иметь в виду при проверке правильности составлений дифференциальных уравнений. Для определения вероятности безотказной работы необходимо вероятность отказа 3-го считать поглощающим, и переход из него в работоспособное состояние запрещается.

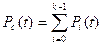
2 случай

;

;

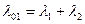
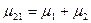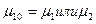
При расчётах по линейному графу необходимо интенсивности переходов выразить через интенсивности отказов и восстановлений.

В основном составе работают 2 элемента, т.е. переход в первое состояние может произойти за счёт любого из них. Вероятность этого перехода будет больше, чем в случае одного работающего элемента. Аналогично и для процесса восстановления. Но если ремонтная бригада одна, то интенсивности переходов везде будут равны интенсивности восстановления одного элемента.

10.7. Расчёт надёжности резервированной аппаратуры в стационарном режиме по линейному графу переходов

При потоках отказов и восстановлений в аппаратуре довольно быстро наступает стационарный режим, при котором вероятности состояний становятся постоянными величинами. В этом случае во всех уравнениях в левой части будут нули.

; ;

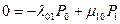
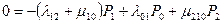
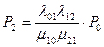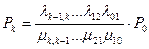
Вероятность k-го состояния есть произведение некого коэффициента на вероятность основного состояния. Коэффициент равен дроби, числитель которой есть произведение интенсивностей переходов (отказов), стоящих над стрелками, идущими вправо от основного состояния до k-го. Знаменатель есть произведение интенсивностей переходов (восстановлений), стоящих под стрелками, идущими влево от k-го состояния до основного.

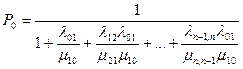
А. аппаратура ремонтируемая

1) Имеется приоритет отказа

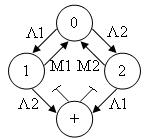Применяем преобразование Лапласа

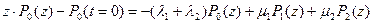
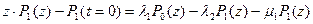
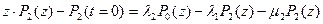
z=0; T=P(z);

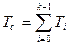
2) Без приоритета отказа

;

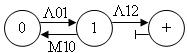
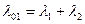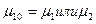
Б. аппаратура неремонтируемая

Расчёт классическим методом

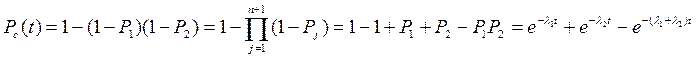
Закон не экспоненциален

;

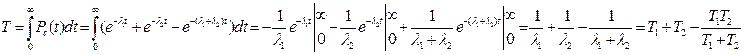
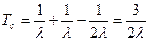Дата добавления: 2013-12-13